CapII-pg4

CapII-pg5

CapIII-pg1

 

Listaremos agora as quatro propriedades que exigiremos que as superfícies tenham. A partir de agora, quando falarmos "superfície", estará implícito que essas quatro propriedades devem ser satisfeitas.

 

Todo ponto de uma superfície ou é interior ou é de bordo. No caso de não haver nenhum ponto de bordo, dizemos que é uma superfície sem bordo. Uma superfície é sempre limitada. Isso significa que existe uma caixa no nosso espaço ambiente que a contém. A caixa pode ser muito grande, mas deve sempre existir! Com isso, ajustando a escala podemos desenhá-la inteiramente. Uma superfície é sempre conexa, isto é, só é formada de um pedaço. Uma superfície é sempre fechada. Veremos abaixo o que isso significa.

 

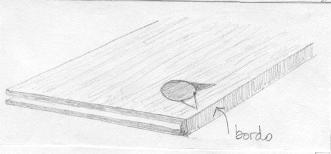
Superfícies fechadas. Na analogia que fizemos, em que Aderbal se move entre duas lâminas de vidro, o bordo representa uma barreira para sua movimentação.

 

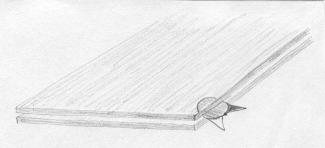
Se não houvesse essa barreira, Aderbal poderia "escapar" da superfície.

 

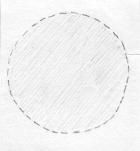
Essas regiões "abertas" por onde Aderbal poderia escapar indicaremos com uma linha pontilhada. Por exemplo, um disco do qual suprimimos os pontos do bordo.

 

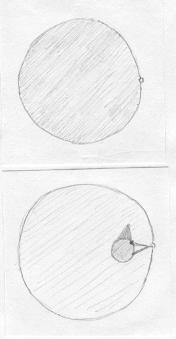
Superfícies com aberturas como essa não são fechadas. Outro exemplo de superfície que não é fechada é o disco do qual suprimimos um ponto só do seu bordo.

 

Neste caso, Aderbal não pode escapar da superfície, pois teria que emagrecer infinitamente. Mesmo assim, pode colocar a ponta da antena exatamente no ponto que não pertence a ela.

 

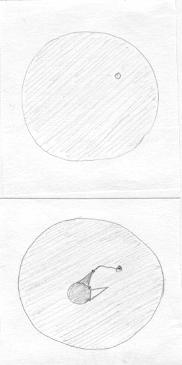
Aderbal pode verificar se uma superfície não é fechada usando uma varinha na ponta da antena. A varinha é maleável mas não pode atravessar bordos.

 

Se uma superfície não é fechada, então é sempre possível posicionar a varinha de modo que sua extremidade não esteja na superfície. Em superfícies fechadas isso não é possível.

 

CapII-pg4

CapII-pg5

CapIII-pg1