(This page in english.)

(Clique aqui para os fontes da implementação de SH e os fontes da dissertação.)

Introdução sobre o problema do teste de planaridade e seus principais algoritmos

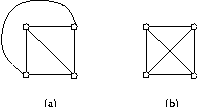
Existem situações práticas onde é necessário determinar se um dado grafo pode ser desenhado no plano de tal forma que suas arestas só se intersectem nos pontos extremos. Um desenho desse tipo é chamado de desenho plano do grafo e um grafo para o qual existe um desenho plano é dito planar (veja figura 1). Por exemplo, em projetos de circuitos VLSI, existe o interesse em obter-se um desenho plano de um grafo que representa um circuito elétrico.

Figure 1: (a) Um desenho plano de um grafo planar. (b) Um desenho que não é plano do mesmo grafo.

Uma caracterização muito simples de grafos planares foi dada por Kuratowski [8]. Ele demonstrou que todo grafo que não é planar contém uma subdivisão do grafo $K_{3,3}$ ou do grafo $K_5$ (veja figura 2). Reciprocamente, nenhum grafo planar contém subdivisões de tais grafos. Uma subdivisão de $K_{3,3}$ ou $K_5$ contida num grafo é chamada de subgrafo de Kuratowski.

Figure 2: (a) Grafo $K_{3,3}$. (b) Grafo $K_5$. (c) Uma subdivisão de $K_{3,3}$.

Apesar de elegante, a caracterização de Kuratowski não fornece um algoritmo muito prático para teste de planaridade. Ademais, não está claro como obter um desenho plano de um grafo planar através dessa caracterização.

Uma possível estratégia para decidir se um grafo $G$ é planar é construir incrementalmente um desenho plano de $G$. Se for possível completar a construção de um desenho plano de $G$, então $G$ é planar, caso contrário, idealmente, um subgrafo de Kuratowski é encontrado em $G$, justificando a não planaridade de $G$. O primeiro algoritmo incremental para teste de planaridade foi proposto por Auslander e Parter [1]. Dado um grafo $G$, primeiramente, um circuito de $G$ é encontrado. O grafo resultante da remoção desse circuito de $G$ é composto de `partes' conexas. O algoritmo é chamado recursivamente para obter um desenho plano de cada uma dessas partes junto com o circuito. Depois, esses desenhos planos são combinados, se possível, para obter um desenho plano de $G$. Se não for possível combinar esses desenhos planos, um subgrafo de Kuratowski é encontrado em $G$. O algoritmo de Auslander e Parter continha um erro que foi corrigido por Goldstein [6], resultando no algoritmo de Auslander, Parter e Goldstein (APG). A complexidade de tempo desse algoritmo é cúbica.

Lempel, Even e Cederbaum [9] (LEC) apresentaram uma maneira alternativa de se construir um desenho plano incrementalmente. Eles começam com o desenho de um único vértice e adicionam ao desenho todas as arestas incidentes a este vértice. Depois adicionam um novo vértice incidente a uma das arestas já inseridas e todas as arestas incidentes a este novo vértice. O processo continua dessa maneira. Cada iteração do algoritmo começa com um desenho plano de parte do grafo e consiste em adicionar um novo vértice e todas as arestas incidentes a este vértice ao desenho plano corrente. O processo continua até que todo o grafo tenha sido desenhado no plano ou tenha-se detectado que o grafo não é planar. Este tipo de algoritmo incremental é chamado de vertex addition algorithm. Tarjan [13] apresentou uma implementação do algoritmo de LEC que consome tempo quadrático.

Em 1974, Hopcroft e Tarjan [7] apresentaram o primeiro algoritmo linear para decidir se um dado grafo é planar. O algoritmo de Hopcroft e Tarjan é uma implementação envolvente do algoritmo de APG.

Hopcroft e Tarjan não deram muitos detalhes de como o seu algoritmo de teste de planaridade pode ser estendido para construir de fato um desenho plano do grafo dado. Uma descrição completa da fase de construção de um desenho plano por esse algoritmo foi feita por Mehlhorn e Mutzel [10] e a respectiva implementação por Mutzel [11]. Até hoje não se conhece uma implementação do algoritmo de Hopcroft e Tarjan que, em tempo linear, devolve um certificado de não planaridade, ou seja, um subgrafo de Kuratowski de um grafo não-planar.

Em 1976, Booth e Lueker [2] apresentaram uma implementação do algoritmo de LEC que consome tempo linear. Para isto, Booth e Lueker empregaram uma estrutura de dados chamada de PQ-árvore. Recentemente, Shih e Hsu [12] e Boyer e Myrvold [3] descreveram implementações similares para o algoritmo de LEC. Ambas gastam tempo linear e evitam o uso de PQ-árvores.

Os dois algoritmos lineares para teste de planaridade mais discutidos na literatura são os algoritmos de APG e o de LEC. Canfield e Williamson [4] fazem uma comparação entre esses dois algoritmos argumentando que os dois, geralmente vistos como métodos bem diferentes, têm na realidade muitas semelhanças.

A figura 3 mostra um resumo do consumo de tempo de algumas implementações dos principais algoritmos de planaridade existentes até hoje.

Figure: Tabela dos principais algoritmos de planaridade e algumas de suas implementações.

Referências Bibliográficas

1

L. Auslander e S.V. Parter, On imbeddings graphs in the plane, J. Math. and Mech. 10 (1961), no. 3, 517-523.

2

K.S. Booth e G.S. Lueker, Testing the consecutive ones property, interval graphs, and graph planarity using PQ-tree algorithms, Journal of Computer and System Science 13 (1976), 335-379.

3

J. Boyer e W. Myrvold, Stop minding your P's and Q's: A simplified planar embedding algorithm, Procedding of the Tenth Annual ACM-SIAM Symposium on Discrete Algorithms (Baltimore, Maryland), ACM Special Interest Group on Algorithms and Computation Theory and SIAM Activity Group on Discrete Mathematics, ACM Press, January 1999, pp. 140-146.

4

E.R. Canfield e S.G. Williamson, The two basic linear time planarity algorithms: Are they the same?, Linear and Multilinear Algebra 26 (1990), 243-265.

5

K. Mehlhorn e St. Näher, The LEDA Platform of Combinatorial and Geometric Computing, Cambridge University Press, 1999.

6

A.J. Goldstein, An efficient and constructive algorithm for testing whether a graph can be embedded in a plane, Graph and Combinatorics Conference, Dept. Math., Princeton University, 1963, pp. 16-18.

7

J. Hopcroft e R. Tarjan, Efficient planarity testing, Journal of the Association for Computing Machinery 21 (1974), no. 4, 549-568.

8

C. Kuratowski, Sur le probleme des corbes gauches en topologie, Fundamenta Mathematicae 15 (1930), 271-283.

9

A. Lempel, S. Even e I. Cederbaum, An algorithm for planarity testing of graphs, Proceddings International Symposium on Theory of Graphs (New York) (P. Rosenstiehl, ed.), Gordon and Breach, July 1967, pp. 215-232.

10

K. Mehlhorn e P. Mutzel, On the embedding phase of the Hopcroft and Tarjan planarity testing algorithm, Algorithmica 16 (1996), no. 2, 233-242.

11

P. Mutzel, A fast embedding algorithm based on the Hopcroft-Tarjan planarity test, Tech. Report 92.107, Universität zu Köln, 1992,
http://www.mpi-sb.mpg.de/~ mutzel/mpireports/publications.html.

12

W.-K. Shih e W.-L. Hsu, A new planarity test, Theoretical Computer Science 223 (1999), 179-191.

13

R.E. Tarjan, Implementation of an efficient algorithm for planarity testing of graphs, Dec. 1969.