(Esta página em português.)

(Click here for the sources of SH algorithm and the sources of the master's dissertation.)


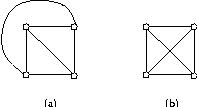
Introduction to the planarity testing problem and related algorithms

Sometimes is useful to determine if a given graph can be drawn in the plane with no crossing edges. Such a drawing is plane. Given a graph, if there is a plane drawing for the graph then the graph is planar (see figure 1). For instance, in VLSI circuits, is useful to obtain a plane drawing of a graph representing an electric circuit.

Figure 1: (a) A plane drawing of a planar graph. (b) Another drawing (not plane) for the same graph.

A simple characterization for planar graphs was given by Kuratowski [8]. He showed that every non-planar graph has a subdivision of $K_{3,3}$ or a subdivision of $K_5$ (see figure 2). Conversely, no planar graph has a subdivision of such graphs. A subdivision of $K_{3,3}$ or $K_5$ in a graph is a Kuratowski's subgraph.

Figure 2: (a) $K_{3,3}$. (b) $K_5$. (c) A subdivision of $K_{3,3}$.

Although elegant, the Kuratowski's characterization doesn't give a practical algorithm for planarity testing. Besides, it is not clear how to calculate a plane drawing through this characterization.

A possible strategy to decide if a graph $G$ is planar is increasingly build a plane drawing for $G$. If a plane drawing of $G$ is completed, then $G$ is planar. Otherwise, ideally, a Kuratowski's subgraph is found in $G$, justifying the non-planarity of $G$. The first algorithm using this strategy for planarity testing was proposed by Auslander and Parter [1]. Given a graph $G$, the algorithm begins finding a circuit in $G$. The resulting graph removing this circuit from $G$ consists of connected 'parts'. The algorithm is called recursively to obtain a plane drawing for each of these parts plus the circuit. Then, these drawings are combined, if possible, to obtain a plane drawing for $G$. If it is not possible, then a Kuratowski's subgraph is found in $G$. The Auslander and Parter's algorithm had an error which was corrected by Goldstein [6], resulting the Auslander, Parter and Goldstein's algorithm (APG). The complexity time of this algorithm is cubic.

Lempel, Even and Cederbaum [9] (LEC) presented an alternative way to increasingly build a plane drawing of a given graph. This algorithm starts with a drawing of a single vertex and adds to the drawing all the edges incident to that vertice. Then, it adds a new vertice incident to an added edge and all the edges incident to this new vertice. The process continues as the following. Each iteration begins with a plane drawing of part of the graph and consists of adding a new vertice and all edges incident to this vertice to the current plane drawing. The process continues until the graph has been completely drawn in the plane or the graph has been detected as non-planar. This kind of algorithm is a vertex addition algorithm. Tarjan [13] presented an implementation for LEC wich runs in quadractic time.

In 1974, Hopcroft and Tarjan [7] presented the first linear-time algorithm to decide if a graph is planar. This algorithm is an implementation for APG's algorithm.

Hopcroft and Tarjan (HT) didn't give much details of how their planarity testing algorithm can be extended to calculate a plane drawing of the given graph. A complete description of this phase of this algorithm was done by Mehlhorn and Mutzel [10] and the respective implementation by Mutzel [11]. So far, there isn't a known linear-time implementation for HT's algorithm that calculates Kuratowski's subgraphs for non-planar graphs.

In 1976, Booth and Lueker [2] presented a linear-time implementation for LEC's algorithm, using a data structure named PQ-tree. Recently, Shih and Hsu [12] and Boyer and Myrvold [3] described similar implementations for LEC's algorithm. Both run in linear-time and avoid using PQ-trees.

The two most discussed algorithms are APG's and LEC's. Canfield and Williamson [4] compare these two algorithms and argument that, at the same time these algorithms are seen as different methods, they have many similarities.

Figure 3 shows a summary of the running time of the main planarity algorithms available nowadays.

Figure: The two most discussed algorithms (APG's and LEC's) and their main implementations.
\begin{figure}\begin{center} \begin{tabular}{\vert l\vert rr\vert} \hline\hline ... ...cite{shih:tcs-223-179} & linear \hline \end{tabular} \end{center}\end{figure}





Bibliography

1
L. Auslander e S.V. Parter, On imbeddings graphs in the plane, J. Math. and Mech. 10 (1961), n. 3, 517-523.

2
K.S. Booth e G.S. Lueker, Testing the consecutive ones property, interval graphs, and graph planarity using PQ-tree algorithms, Journal of Computer and System Science 13 (1976), 335-379.

3
J. Boyer e W. Myrvold, Stop minding your P's and Q's: A simplified planar embedding algorithm, Procedding of the Tenth Annual ACM-SIAM Symposium on Discrete Algorithms (Baltimore, Maryland), ACM Special Interest Group on Algorithms and Computation Theory and SIAM Activity Group on Discrete Mathematics, ACM Press, January 1999, pp. 140-146.

4
E.R. Canfield e S.G. Williamson, The two basic linear time planarity algorithms: Are they the same?, Linear and Multilinear Algebra 26 (1990), 243-265.

5
K. Mehlhorn e St. Näher, The LEDA Platform of Combinatorial and Geometric Computing, Cambridge University Press, 1999.

6
A.J. Goldstein, An efficient and constructive algorithm for testing whether a graph can be embedded in a plane, Graph and Combinatorics Conference, Dept. Math., Princeton University, 1963, pp. 16-18.

7
J. Hopcroft e R. Tarjan, Efficient planarity testing, Journal of the Association for Computing Machinery 21 (1974), n. 4, 549-568.

8
C. Kuratowski, Sur le probleme des corbes gauches en topologie, Fundamenta Mathematicae 15 (1930), 271-283.

9
A. Lempel, S. Even e I. Cederbaum, An algorithm for planarity testing of graphs, Proceddings International Symposium on Theory of Graphs (New York) (P. Rosenstiehl, ed.), Gordon and Breach, July 1967, pp. 215-232.

10
K. Mehlhorn e P. Mutzel, On the embedding phase of the Hopcroft and Tarjan planarity testing algorithm, Algorithmica 16 (1996), n. 2, 233-242.

11
P. Mutzel, A fast embedding algorithm based on the Hopcroft-Tarjan planarity test, Tech. Report 92.107, Universität zu Köln, 1992,
http://www.mpi-sb.mpg.de/~ mutzel/mpireports/publications.html.

12
W.-K. Shih e W.-L. Hsu, A new planarity test, Theoretical Computer Science 223 (1999), 179-191.

13
R.E. Tarjan, Implementation of an efficient algorithm for planarity testing of graphs, Dec. 1969.