Análise de Algoritmos | Aulas | Dicionário | Índice

Complexidade da ordenação

Outras páginas deste sítio trataram da complexidade de algoritmos. Esta página tratará da complexidade intrínseca de um problema.

Problema da ordenação:  Rearranjar um vetor A[1 .. n] de modo que ele fique em ordem crescente.

Qual a complexidade computacional do problema da ordenação? Em outras palavras, qual o consumo de tempo (no pior caso) do melhor algoritmo possível para o problema da ordenação?

Esta página é baseada na seção 8.1 (Lower bounds for sorting) do livro de CLRS.

Algoritmos baseados em comparações

No pior caso, o algoritmo de inserção e o algoritmo Quicksort consomem Ο(n²) unidades de tempo para resolver o problema da ordenação. O algoritmo Mergesort consome Ο(n lg n) unidades de tempo. O algoritmo RadixSort consome apenas Ο(n) unidades de tempo, mas esse algoritmo é muito diferente dos anteriores pois resolve o problema sem fazer comparações entre elementos do vetor e supõe que os dados satisfazem certas hipóteses.

É natural perguntar então qual a complexidade do problema de ordenação (no sentido assintótico) se nos restringirmos a algoritmos baseados em comparações, ou seja, algoritmos que consistem em comparar entre si os elementos do vetor A[1 .. n].

Mostraremos a seguir que qualquer algoritmo baseado em comparações executa pelo menos ½ n lg n comparações entre elementos do vetor no pior caso e portanto consome

Ω(n lg n)

unidades de tempo.

Árvores de decisão

Todo algoritmo de ordenação baseado em comparações pode ser representado, abstratamente, por uma árvore de decisão (= decision tree). Trata-se de uma árvore binária cada um de cujos nós internos representa a comparação entre dois elementos específicos — como A[5] e A[121], por exemplo — do vetor. Nessa representação abstrata não há movimentação de elementos do vetor; a árvore procura apenas decidir qual das n! permutações do vetor está em ordem crescente. Cada folha da árvore corresponde a uma dessas n! permutações. Como estamos tratando do pior caso, vamos supor que os elementos do vetor são distintos dois a dois.

Digamos que um nó interno da árvore compara dois elementos a e b do vetor. O filho esquerdo do nó corresponde ao caso em que a ≤ b, e o filho direito ao caso em que a > b. A raiz da árvore representa a primeira comparação que o algoritmo faz.

Exemplo A:  Considere o algoritmo Ordenação-por-Inserção, reproduzido a seguir. O algoritmo gira em torno da comparação A[i] > x na linha 4, sendo x uma cópia de um elemento do vetor.

Ordenação-por-Inserção (A, n)

1 . para j := 2 até n

2 .ooo x := A[j]

3 .ooo i := j − 1

4 .ooo enquanto i > 0 e A[i] > x

5 .oooooo A[i+1] := A[i]

6 .oooooo i := i − 1

7 .ooo A[i+1] := x

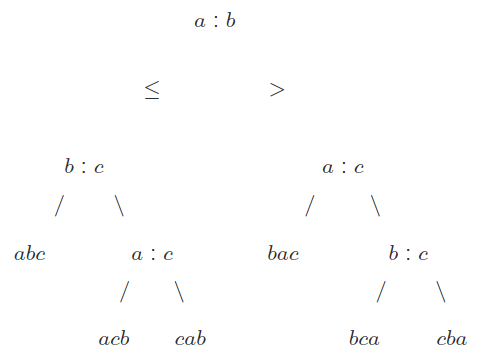
Suponha que o algoritmo é aplicado a um vetor A[1 .. 3] cujos elementos são diferentes dois a dois. Suponha que a, b e c são os valores originais de A[1] e A[2], A[3] respectivamente. Veja agora a árvore de decisão, supondo que uma expressão como a : b representa uma comparação entre a e b; e uma expressão como bac significa que b < a < c.

Qualquer execução do algoritmo é representada com um caminho que vai da raiz da árvore até uma folha.

De uma maneira geral, se uma árvore de decisão representa um algoritmo de ordenação aplicado a um vetor A[1 .. n] sem elementos repetidos, então

1. cada folha da árvore corresponde a uma permutação dos elementos de A[1 .. n],
2. cada uma da n! permutações está representada em alguma folha,
3. toda execução do algoritmo é um caminho que vai da raiz até uma folha.

Como a árvore tem pelo menos n! folhas, a altura da árvore (ou seja, o comprimento do mais longo caminho que vai da raiz até uma folha) deve ser suficientemente grande. Como uma árvore de altura h tem no máximo 2^h folhas, temos 2^h ≥ n!, donde

h ≥ lg (n!) .

Queremos mostrar que lg (n!) ≥ ½ n lg n. Para isso, será preciso verificar preliminarmente que −i² + ni − i + n ≥ n para todo i no intervalo 0 .. n−1. Feito esse cálculo, observe que

Logo,  n! ≥ n^n/2  e portanto h ≥ lg (n^n/2) ≥ ½ n lg n .

Concluímos assim que qualquer algoritmo de ordenação baseado em comparações faz pelo menos  ½ n lg n comparações entre elementos do vetor no pior caso. Segue daí que qualquer algoritmo desse tipo consome

Ω(n lg n)

unidades de tempo no pior caso.