Algoritmos para Grafos  |  Índice

Emparelhamentos em grafos bipartidos

Este capítulo apresenta o problema do emparelhamento máximo em grafos não-dirigidos.  Em seguida, resolve o problema em grafos não-dirigidos bipartidos.  (Em grafos não-dirigidos arbitrários, o problema é mais difícil.)

Emparelhamentos

Um emparelhamento (= matching) num grafo não-dirigido é um conjunto de arestas sem pontas em comum.  Em outras palavras, um emparelhamento é um conjunto M de arestas com a seguinte propriedade: o leque de cada vértice tem no máximo uma aresta de M.

É fácil encontrar emparelhamentos pequenos: o conjunto vazio, por exemplo, é um emparelhamento. É mais difícil encontrar emparelhamentos grandes. É especialmente difícil encontrar um emparelhamento máximo.

Um emparelhamento M é máximo se não existe outro maior, ou seja, se não existe um emparelhamento M' tal que |M'| > |M|.

Exemplo A.  Imagine um grande projeto a ser executado por muitos times de 2 pessoas. Suponha que um grafo não-dirigido representa as compatibilidades entre as pessoas dispostas a participar do projeto. Um emparelhamento é um conjunto de times que respeita as compatibilidades.

Caminhos alternantes

Dado um emparelhamento num grafo não-dirigido, como obter um emparelhamento maior?  A resposta passa pelo conceito de caminho alternante. Antes de introduzir esse conceito, precisamos de um pouco de terminologia.

Suponha dado um emparelhamento M.  Se uma aresta v-w pertence a M, dizemos que v e w estão emparelhados ou casados.  Um vértice v é solteiro se o leque de v não contém arestas de M.

Como estamos tratando de grafos não-dirigidos, será necessário restringir um pouco a definição de caminho.  Caminhos como  a-b-a-c-a-d  e  a-b-c-d-e-c-b-d,  por exemplo, serão excluídos.  Mais precisamente, usaremos apenas caminhos que têm a seguinte propriedade: se um arco v-w pertence ao caminho então o arco antiparalelo w-v não pertence ao caminho. (Vale lembrar que, por definição, caminhos não têm arcos repetidos.)  Uma aresta v-w pertence ao caminho se v-w ou w-v é arco do caminho.

Um caminho é alternante (= alternating) em relação a um emparelhamento M se for simples e se suas arestas estiverem alternadamente em M e fora de M.  Um caminho alternante é aumentador (= augmenting) se começa e termina num vértice solteiro e tem comprimento maior que 0.

Dado um emparelhamento M e um caminho aumentador P, considere o conjunto de arestas (M − E_P) ∪ (E_P − M), onde E_P o conjunto de arestas de P.  Esse conjunto é conhecido como diferença simétrica, ou OU exclusivo, de M e E_P.  Esse conjunto será indicado por  M⊕P  a pode ser descrito assim: tire de M todas arestas de P que estão em M e acrescente a M todas as arestas de P que não estão em M.  É fácil verificar que

1. M⊕P  é um emparelhamento
2. M⊕P é maior que M.

Segue daí a ideia de um algoritmo iterativo para o problema do emparelhamento máximo.  Cada iteração do algoritmo começa com um emparelhamento M. Cada iteração encontra um caminho aumentador P. A iteração seguinte começa com M⊕P no papel de M.  Se não houver caminho aumentador, o processo para.  Quando isso acontece, o emparelhamento M é máximo!

Exemplo B.  Considere o grafo que tem arestas  0-1 1-2 2-3 3-0 4-5 5-6 6-7 7-4 0-4 1-5 2-6 3-7.  Comece com um emprelhamento vazio. Veja uma sequência de caminhos aumentadores que leva a um emparelhamento máximo:

0-1
2-6
4-0-1-5
3-0-4-7

Representação de emparelhamentos

Antes de pensar em implementar algoritmos, é preciso inventar uma boa maneira de representar um emparelhamento.  Uma simples lista das arestas do emparelhamento não basta. Precisamos de uma representação que amarre cada vértice com a aresta do emparelhamento que incide naquele vértice.

Usaremos um vetor  match[]  de vértices indexado por vértices para representar um emparelhamento.  Se o emparelhamento casa v com w, teremos  match[v] ≡ w  e  match[w] ≡ v.  É como se match[] cuidasse de cada arco da aresta em separado.  Se v é solteiro, adotaremos a convenção match[v] ≡ -1.  É claro que vale a seguinte propriedade: se match[v] ≠ -1 então  match[match[v]] ≡ v.

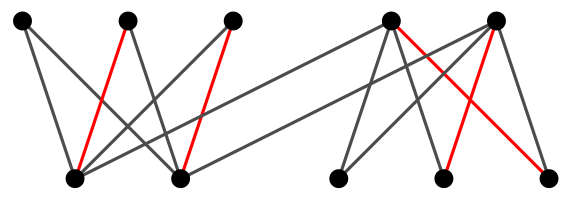
Exemplo C.  No grafo não-dirigido da figura, suponha que os vértices da primeira linha sejam  0 1 2 3 4  e os da segunda linha sejam  5 6 7 8 9 , sempre da esquerda para a direita.  Então o emparelhamento vermelho é representado pelo vetor

      v   0 1 2 3 4 5 6 7 8 9
match[v]  - 5 6 9 8 1 2 - 4 3

com - indicando -1.

Cálculo da diferença simétrica

A representação de emparelhamentos que acabamos de adotar permite calcular M⊕P de maneira muito rápida.  Dado um emparelhamento M, suponha que P é um caminho aumentador que começa num vértice s e termina num vértice t (é claro que s e t são colteiros).  Suponha que o caminho é representado por um vetor pa[]: para cada vértice w do caminho, pa[w] é o vértice anterior a w no caminho. Suponha também que pa[s] ≡ s.  Então, se M é representado por um vetor match[], a seguinte função calcula M⊕P modificando match[] à medida que percorre P do fim para o começo.

static vertex pa[1000];

/* Esta função 
   executa a operação M⊕P sobre um emparelhamento M e 
   um caminho aumentador P. 
   O emparelhamento é representado pelo vetor match[0..V-1]
   e o caminho é representado por um vetor pa[0..V-1].
   O término de P é t.
   A origem de P não é dada explicitamente
   mas caracterizada pela propriedade
   pa[s] == s. */

static void newMatching( vertex *match, vertex t) 
{ 
   vertex x;
   do {
      x = pa[t];
      match[t] = x;
      match[x] = t;
      t = pa[x]; 
   } while (t != x);
}

Em cada iteração, a aresta t-x é acrescentada ao emparelhamento e a aresta x-pa[x] é retirada do emparelhamento:

      .   .   x           .   x   .
       \ / \ / \           \ / \ / \
        .   .   t           .   t   .

Algoritmo húngaro

Todos os conceitos, definições e observações feitos até aqui aplicam-se a qualquer grafo não-dirigido.  A partir deste ponto, entretanto, vamos nos limitar a grafos bipartidos, pois encontrar caminhos aumentadores em grafos não-dirigidos arbitrários é bem mais difícil.

A seguinte função implementa o algoritmo do emparelhamento máximo esboçado acima. O coração (ou será cérebro?) da implementação é a função auxiliar augmentMatching().

#define UGraph Graph

/* Esta função 
   calcula um emparelhamento máximo M no grafo não-dirigido 
   bipartido G.
   A bipartição de G é dada pelo vetor color[0..V-1],
   que tem valores 0 e 1.
   A função devolve o tamanho de M
   e armazena uma representação de M no vetor match[0..V-1]: 
   para cada vértice v, 
   match[v] é o vértice que M casa com v 
   (ou -1 se v é solteiro).
   (Essa função não está no livro de Sedgewick.) */

int UGRAPHbipMatching( UGraph G, int *color, vertex *match) 
{ 
   for (vertex v = 0; v < G->V; ++v) match[v] = -1;
   int size = 0;
   while (augmentMatching( G, color, match))
      size++;
   return size;
}

A missão da função booleana auxiliar augmentMatching() é encontrar um caminho aumentador para o emparelhamento representado por match[].  Para procurar por um caminho aumentador, a função faz uma busca em largura modificada. (Poderia também fazer uma busca em profundidade.)  A busca começa, simultaneamente, em todos os vértices solteiros de cor 0 e anda dois passos de cada vez:

• primeiro, percorre uma aresta que não está no emparelhamento;
• depois, percorre uma aresta do emparelhamento.

A busca constrói uma floresta BFS alternante cujas raízes são os vértices solteiros de cor 0. A floresta é alternante porque todos os caminhos na floresta são alternantes. Se essa floresta atingir um vértice solteiro de cor 1 teremos encontrado um caminho aumentador.

static vertex pa[1000];
static bool visited[1000];

/* Esta função recebe um grafo não-dirigido bipartido G,
   com bipartição color[0..V-1],
   e um emparelhamento M representado
   por match[0..V-1]. 
   A função procura calcular um emparelhamento maior que M.
   Se tiver sucesso, devolve true 
   e modifica match[] de acordo.
   Se fracassar, devolve false sem alterar match[]. 
   (A função usa a estratégia de busca em largura.
   Essa função não está no livro de Sedgewick.) */

static bool augmentMatching( UGraph G, int *color, vertex *match) 
{ 
   for (vertex v = 0; v < G->V; ++v) visited[v] = false;
   QUEUEinit( G->V);
   for (vertex s = 0; s < G->V; ++s) {
      if (color[s] == 0 && match[s] == -1) {
         visited[s] = true; 
         pa[s] = s;
         QUEUEput( s); 
      }
   } 
   // a fila contém todos os vértices solteiros de cor 0

   while (!QUEUEempty( )) { 
      // color[v] == 0 para todo v na fila
      vertex v = QUEUEget( );
      for (link a = G->adj[v]; a != NULL; a = a->next) {
         vertex w = a->w; // color[w] == 1
         if (!visited[w]) { 
            visited[w] = true; 
            pa[w] = v; 
            if (match[w] == -1) { // caminho aumentador!
               newMatching( match, w);
               QUEUEfree( );
               return true;
            }
            vertex x = match[w]; // visited[x] == false
            visited[x] = true;
            pa[x] = w; // caminho ganhou segmento v-w-x
            QUEUEput( x); 
         }
      }
   }

   QUEUEfree( );
   return false;
}

Não é difícil verificar que a função augmentMatching() está correta.  É fácil deduzir daí que UGRAPHbipMatching() produz um emparelhamento.  Não é óbvio, entretanto, que o emparelhamento produzido pela função é máximo. Cuidaremos disso na próxima seção.

Desempenho.  O consumo de tempo da função augmentMatching() é essencialmente igual ao de uma busca BFS, ou seja, proporcional ao tamanho do grafo.  A função UGRAPHbipMatching() invoca augmentMatching() tantas vezes quanto é o tamanho de um emparelhamento máximo, portanto no máximo V/2 vezes.  Logo, o consumo de tempo de UGRAPHbipMatching() é proporcional a V (V + E) no pior caso.  (Como de hábito, V é o número de vértices e E é o número de arestas do grafo.)

Coberturas (de arestas por vértices)

Passamos a tratar agora de um problema que parece não ter relação alguma com emparelhamentos, mas vai levar à prova de que o emparelhamento calculado pelo algoritmo dos caminhos aumentadores é máximo.

Uma cobertura (= vertex cover) de um grafo não-dirigido G é um conjunto de vértices que contém pelo menos uma ponta de cada aresta de G.  (Essa definição vale em qualquer grafo não-dirigido, seja ele bipartido ou não.)

Coberturas grandes são fáceis de encontrar: o conjunto de todos os vértices do grafo, por exemplo, é uma cobertura.  É bem mais difícil encontrar coberturas pequenas.  É especialmente difícil encontrar uma cobertura mínima. (Uma cobertura K é mínima se não existe outra cobertura K' tal que |K'| < |K|.)

Exemplo D.  No grafo não-dirigido da figura, suponha que os vértices da primeira linha sejam  0 1 2 3 4  e os da segunda linha sejam  5 6 7 8 9 ,  sempre da esquerda para a direita.  O conjunto de vértices  0 1 2 3 4   é uma cobertura.  O conjunto   3 4 5 6   também é uma cobertura.  Mostre que essa cobertura é mínima!

Exemplo E.  As obras de arte de uma galeria ficam expostos ao longo de vários corredores retos. Nos cruzamentos de corredores há pequenas praças. Quero colocar guardas nas praças, no máximo um guarda em cada praça, de modo que todos os corredores sejam vigiados. Qual o menor número de guardas necessário?

Cobertura mínima.  Há uma relação simples entre coberturas e emparelhamentos: para qualquer cobertura K e qualquer emparelhamento M em qualquer grafo não-dirigido, tem-se

|K| ≥ |M|.

Portanto, se |K| = |M| então a cobertura K é mínima e o emparelhamento M é máximo.

Temos aí um meio de provar que um dado emparelhamento M é máximo:  basta exibir uma cobertura com apenas |M| vértices!  (Compare a relação entre emparelhamentos e coberturas com a De acordo com relação entre distâncias e potenciais viáveis e com a relação entre coloração de vértices e cliques. Essas desigualdades são manifestações do fenômeno da dualidade em programação linear.)

Em geral uma cobertura mínima é maior que um emparelhamento máximo.  No caso de grafos não-dirigidos bipartidos, entretanto, vale a igualdade, como passamos a demonstrar.  Suponha que a última iteração do algoritmo dos caminhos aumentadores começa com um emparelhamento M.  Seja X o conjunto dos vértices visitados na tentativa frustrada de encontrar um caminho aumentador. Em outras palavras, X é o conjunto dos términos de todos os caminhos alternantes que começam em vértices solteiros de C₀, sendo C₀ o conjunto dos vértices s tais que color[s] ≡ 0.  Então a diferença simétrica (X − C₀) ∪ (C₀ − X), que denotaremos por

X ⊕ C₀ ,

é uma cobertura. E essa cobertura tem o mesmo tamanho que o emparelhamento M. (Esses dois fatos não são óbvios, mas são fáceis de provar.)

Podemos dizer, então, que o algoritmo dos caminhos aumentadores prova o seguinte teorema de Kőnig-Egerváry: num grafo bipartido, um emparelhamento M é máximo se e somente se existe uma cobertura K tal que |M| ≡ |K|.

É fácil estender o código de UGRAPHbipMatching() para que a função produza não só um emparelhamento como também uma cobertura do mesmo tamanho que o emparelhamento. O vetor característico cover[] da cobertura pode ser calculado assim no fim de UGRAPHbipMatching():

   for (vertex v = 0; v < G->V; ++v) 
      if (color[v] == 1 && visited[v] || 
          color[v] == 0 && !visited[v]) 
         cover[v] = true;
      else cover[v] = false;

A cobertura definida por cover[] é um certificado de maximalidade do emparelhamento e o emparelhamento é um certificado de minimalidade da cobertura.  Essa versão modificada de UGRAPHbipMatching() é, portanto, autocertificada. 

Conclusão

Este capítulo traz mais uma caracterização demonstrada por um algoritmo. As três caracterizações desse tipo vistas até aqui são:

• Um grafo é topológico se e somente se não tem ciclos.
• Um grafo não-dirigido é bipartido se e somente se não tem circuito ímpar.
• Num grafo bipartido, um emparelhamento é máximo se e somente se tem o mesmo tamanho que uma cobertura.

A primeira caracterização foi demonstrada pela função GRAPHcycle0().  A segunda é demonstrada pela função UGRAPHtwoColor(). A terceira é demonstrada pela função UGRAPHbipMatching() somada ao fragmento de código que calcula uma cobertura mínima.