Algoritmos para Grafos  |  Índice

Grafos

Este capítulo define o objeto combinatório conhecido como grafo, ou grafo dirigido, ou ainda grafo orientado. Grafos são importantes modelos para uma grande variedade de problemas de engenharia, computação, matemática, economia, biologia, etc.

Definições básicas

Um  grafo  (= graph) é um par de conjuntos: um conjunto de coisas conhecidas como vértices e um conjunto de coisas conhecidas como arcos. Cada arco é um par ordenado de vértices. O primeiro vértice do par é a ponta inicial do arco e o segundo é a ponta final.

Os arcos dos grafos são dirigidos: cada arco começa na sua ponta inicial e termina na sua ponta final. Para enfatizar esse fato, usamos ocasionalmente a expressão grafo dirigido (= directed graph) no lugar de grafo, embora o adjetivo dirigido seja redundante. (Alguns livros usam o termo digrafo. Esse termo é uma tradução de digraph, que resultou da contração de directed e graph.)

A ponta final de todo arco é diferente da ponta inicial. Um arco com ponta inicial v e ponta final w será denotado por

v-w .

(Não confunda essa expressão com v menos w.)  Dizemos que o arco v-w  sai  de v e  entra  em w. A presença de um arco v-w é independente da presença do arco w-v: o grafo pode ter os arcos v-w e w-v, pode ter apenas um deles, ou pode não ter nenhum deles.

Dizemos que um vértice w é vizinho de um vértice v se v-w é um arco do grafo. Dizemos também, nessa circunstância, que w é adjacente a v. A relação de vizinhança não é simétrica: w pode ser vizinho de v sem que v seja vizinho de w.

O tamanho de um grafo com V vértices e A arcos é a soma V + A.

Exemplo A.  Uma boa maneira de especificar um grafo é exibir o seu conjunto de arcos.  Por exemplo, o conjunto de arcos

0-5 0-6 2-0 2-3 3-6 3-10 4-1 5-2 5-10 
6-2 7-8 7-11 8-1 8-4 10-3 11-8

define um grafo sobre o conjunto de vértices  0..11.  [Este exemplo foi copiado do livro Algorithms, de Sedgewick e Wayne.]

Exemplo B.  A estrutura da rede WWW pode ser representada por um grafo: os vértices são as páginas HTML e os arcos são os links que apontam de uma página para outra. Navegar na rede é pular de um vértice a outro seguindo os arcos.

Arcos antiparalelos e arcos paralelos

Dois arcos são  antiparalelos  se a ponta inicial de um é a ponta final do outro e vice-versa. Em outras palavras, dois arcos são antiparalelos se um é  v-w  e o outro é w-v.

Poderíamos tentar dizer que dois arcos são paralelos (ou repetidos) se têm a mesma ponta inicial e a mesma ponta final. Mas esse conceito não faz sentido sob nossas definições, uma vez que arcos são meros pares de vértices e portanto dois arcos diferentes não podem ter a mesma ponta inicial e a mesma ponta final. Portanto, nossos grafos não têm arcos paralelos.

Leques e graus de vértices

O leque de saída (= fan-out) de um vértice num grafo é o conjunto de todos os arcos que saem do vértice. O leque de entrada (= fan-in) de um vértice é o conjunto de todos os arcos que entram no vértice.

Dado um conjunto X de vértices de um grafo, o leque de saída de X é o conjunto dos arcos que saem de X, ou seja, saem de algum vértice em X e entram em algum vértice fora de X. O leque de entrada de X é o conjunto dos arcos que entram em X.

O grau de saída (= outdegree) de um vértice num grafo é o tamanho do seu leque de saída, ou seja, o número de arcos que saem do vértice. O grau de entrada (= indegree) é o tamanho do leque de entrada do vértice.

Uma fonte (= source) é um vértice que tem grau de entrada nulo. Um sorvedouro (= sink) é um vértice que tem grau de saída nulo.

Um vértice é isolado se seu grau de entrada e seu grau de saída são ambos nulos. É claro que um grafo sem vértices isolados é completamente definido por seu conjunto de arcos.

Número de arcos

É fácil verificar que a soma dos graus de saída de todos os vértices de um grafo é igual ao número de arcos do grafo. A soma dos graus de entrada de todos os vértices também é igual ao número de arcos.  Segue daí que um grafo com V vértices tem no máximo

V (V−1)

arcos. Esse número é apenas um pouco menor que  V².

Um grafo é  completo  se todo par ordenado de vértices distintos é um arco. Um grafo completo com V vértices tem exatamente V (V−1) arcos.  Um torneio é qualquer grafo dotado da seguinte propriedade: para cada par  v w  de vértices distintos, v-w é um arco ou w-v é um arco, mas não ambos. Um torneio com V vértices tem exatamente ½V(V−1) arcos.

Um grafo é denso se tem muitos arcos em relação ao seu número de vértices e esparso se tem poucos arcos. Mais precisamente, um grafo é denso se o seu número de arcos é da mesma ordem que o quadrado do número de vértices, digamos V²/2, ou V²/10, ou V²/100, ou algo assim. (Portanto, o tamanho de um grafo denso é proporcional a V².)  Um grafo é esparso se seu número de arcos é da mesma ordem que V, digamos 10V, ou V/2, ou algo assim.  (Portanto, o tamanho de um grafo esparso é proporcional a V.)  É claro que essas definições não se aplicam a grafos individuais, mas a famílias infinitas de grafos.

Subgrafos

Um sub­grafo de um grafo G é um pedaço de G. O conjunto de vértices e o conjunto de arcos do pedaço de G devem ser coerentes. Assim, é melhor formular o conceito como uma relação entre dois grafos:  Um grafo H é sub­grafo de um grafo G se todo vértice de H é vértice de G e todo arco de H é arco de G. (Notação:  H ⊆ G.)

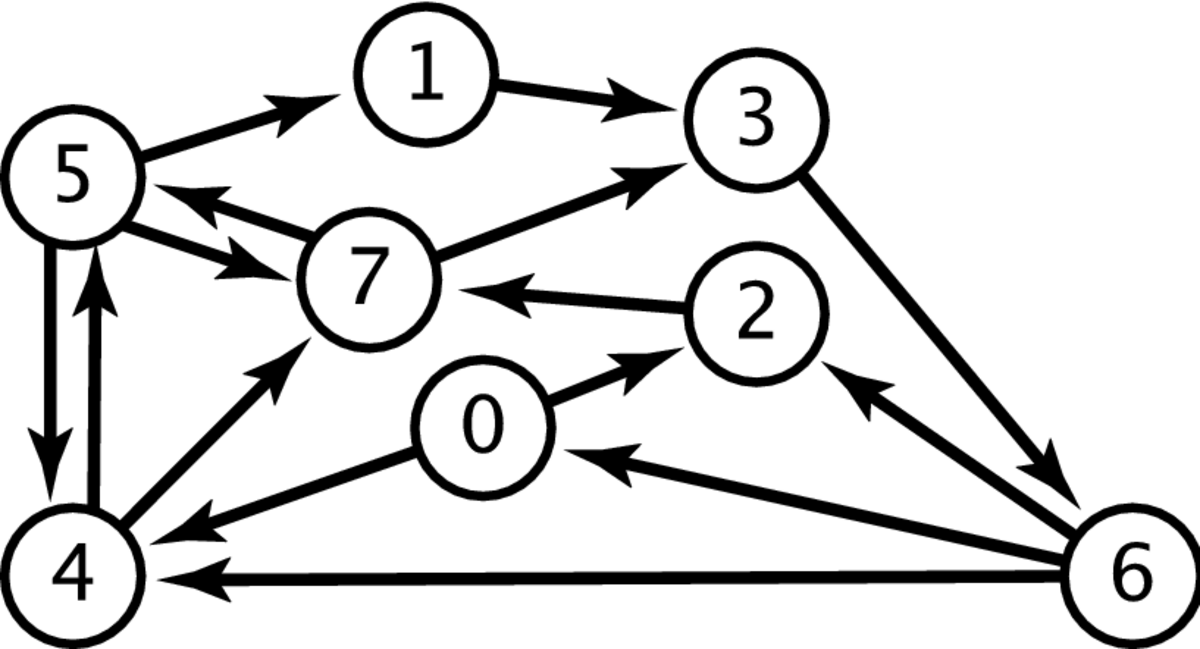
Por exemplo, se G é o grafo definido por todos os arcos da figura e H é o grafo formado apenas pelos arcos escuros, então H ⊆ G. Outro exemplo: o grafo que tem vértices  1 3 5 7  e arcos  1-3 5-1 5-7  é um sub­grafo de H (e também de G). Já os vértices  1 3 5  e os arcos  1-3 5-1 5-7  nem chegam a constituir um grafo.

Alguns tipos de sub­grafos merecem destaque. Um sub­grafo H de um grafo G é

• gerador  (= spanning)  se contém todos os vértices de G,
• induzido se todo arco de G com ambas as pontas em H também é arco de H,
• próprio se for diferente de G  (notação: H ⊂ G).

Dado um conjunto X de vértices de um grafo G, o sub­grafo de G induzido por X  é o sub­grafo formado por X e todos os arcos de G que têm ambas as pontas em X. Esse grafo pode ser denotado por G[X].

Se a é um arco de um grafo G, denotaremos por G−a o sub­grafo que resulta da remoção do arco a de G.

Um supergrafo é o contrário de um sub­grafo: um grafo G é supergrafo de um grafo H se H for sub­grafo de G.

Grafos não-dirigidos

Um grafo é  não-dirigido  (= undirected)  se cada um de seus arcos é antiparalelo a algum outro arco: para cada arco v-w, o grafo também tem o arco  w-v.  Por exemplo, o conjunto de arcos abaixo define um grafo não-dirigido.

0-1 0-2 0-5 1-2 2-3 2-4 3-4 3-5 
1-0 2-0 5-0 2-1 3-2 4-2 4-3 5-3

Num grafo não-dirigido, a relação de adjacência é simétrica: um vértice w é adjacente a um vértice v se e somente se v é adjacente a w. (O mesmo se aplica ao sinônimo vizinho de adjacente.)

         

Convém tratar os pares de arcos antiparalelos de um grafo não-dirigido como uma nova entidade. Assim, diremos que cada par de arcos antiparalelos é uma  aresta  (= edge). Qualquer um dos dois arcos da aresta pode ser usado para representar a aresta. Podemos dizer, então, que

0-1 0-2 0-5 1-2 2-3 2-4 3-4 3-5

é o conjunto de arestas do grafo não-dirigido que aparece no exemplo acima. O número de arestas de um grafo não-dirigido é a metade do seu número de arcos: se  E  denota o número de arestas e  A  denota o número de arcos então  E = A / 2 .  Diremos que uma aresta v-w liga os vértices v e w. Diremos também que v-w incide em v e em w.

Num grafo não-dirigido, o leque de um vértice v é o conjunto de arestas que incidem em v. O grau de v é o número de arestas no leque de v. É claro que o grau de um vértice é igual ao seu grau de entrada e também ao seu grau de saída. É fácil verificar que a soma dos graus de todos os vértices de um grafo não-dirigido vale 2E, sendo E o número de arestas.

Subgrafos.  Um sub­grafo de um grafo não-dirigido pode não ser não-dirigido (pois pode incluir apenas um dos arcos de alguma aresta). Se queremos um sub­grafo não-dirigido, precisamos dizer isso explicitamente.

A propósito, é claro que todo sub­grafo induzido de um grafo não-dirigido é necessariamente não-dirigido.