Algoritmos para Grafos  |  Índice

Caminhos de comprimento mínimo

Qual o caminho mais curto, em número de quarteirões, de um ponto A a um ponto B de uma grande cidade?

Este capítulo é uma introdução geral ao problema do caminho de comprimento mínimo em grafos. Embora corriqueiro, o problema tem sutilezas que precisam ser bem entendidas antes que possamos tentar resolvê-lo. Um bom algoritmo para o problema do caminho mínimo será discutido num próximo capítulo. O presente capítulo tratará apenas de condições necessárias e suficientes de minimalidade bem como de um algoritmo especial para grafos acíclicos.

Caminhos mínimos e distâncias

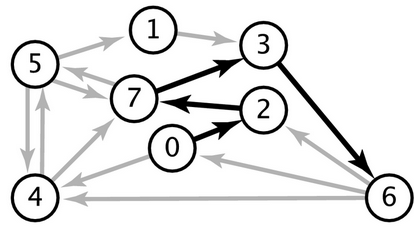
Um caminho C num grafo é mínimo se não existe outro caminho que  tenha a mesma origem e o mesmo término que C mas comprimento menor que o de C. (Vale lembrar que o comprimento é o número de arcos do caminho.)  Na figura acima, por exemplo, o caminho  0-2-7-5-1-3-6  não é mínimo porque o caminho  0-2-7-3-6  é mais curto.

É claro que todo caminho mínimo é simples. (Portanto, o simples na expressão caminho simples mínimo é redundante.)  É claro também que nem toda instância do problema tem solução: se t não está ao alcance de s então não existe caminho algum de s a t.

A  distância  de s a t é o comprimento de um caminho mínimo com origem s e término t. É claro que a distância de s a t é 0 se e somente se s ≡ t. É claro também que a distância de s a t é  d  se e somente se  (1) algum caminho de s a t tem comprimento d  e  (2) todo caminho de s a t tem comprimento pelo menos d. Se não existe caminho algum de s a t, podemos dizer que a distância de s a t é ∞ (infinita).

O conceito de distância é dirigido: a distância de s a t é, em geral, diferente da distância de t a s. Por isso, dizemos distância de s a t e não distância entre s e t.

Exemplo A.  No grafo da figura, o caminho 0-2-7-3-6 tem comprimento 4. Nenhum caminho de 0 a 6 tem comprimento menor que 4. Logo, o caminho 0-2-7-3-6 é mínimo e a distância do vértice 0 ao vértice 6 é 4. Agora considere a distância na direção contrária. Verifique que a distância de 6 a 0 é 1.

Potencial e condições de minimalidade

Para provar que um dado caminho C é mínimo, precisamos mostrar que todo caminho com a mesma origem e o mesmo término que os de C é pelo menos tão comprido quanto C. Para fazer isso, vamos introduzir o conceito de potencial relaxado.

Um potencial para um grafo G é uma numeração dos vértices de G, ou seja, um vetor que associa um número a cada vértice de G. Em relação a um potencial h[ ], dizemos que um arco v-w está tenso se h[w] − h[v]  > 1  e está relaxado se h[w] − h[v]  ≤ 1. Em outras palavras, v-w está tenso h[v] + 1 < h[w]  e está relaxado se

h[v] + 1  ≥  h[w] .

Um potencial é relaxado (ou viável) se deixa todos os arcos de G relaxados.

Qualquer potencial relaxado h[ ] dá uma cota inferior para as distâncias entre vértices: se P é um caminho de um vértice x a um vértice y então |P| ≥ h[y] − h[x], sendo |P| o comprimento de P. (Por exemplo, se P é o caminho 0-1-2-3 então |P| = 1 + 1 + 1 ≥ h[3] − h[2] + h[2] − h[1] + h[1] − h[0] = h[3] − h[0].)  Isso leva à seguinte condição suficiente de minimalidade de um caminho.

A recíproca dessa condição é verdadeira se nos restringirmos aos caminhos mínimos que têm uma origem comum: Para qualquer vértice s, o vetor das distâncias a partir de s é um potencial relaxado. Aqui, o vetor das distâncias a partir de s é o vetor d[ ] definido pela seguinte propriedade: para cada vértice v, d[v] é a distância de s a v.

Exemplo B.  A tabela abaixo dá as distâncias a partir do vértice 5 no grafo da figura. Verifique pacientemente que d[] é o vetor das distâncias a partir de 5.

  v  0 1 2 3 4 5 6 7
d[v] 4 1 4 2 1 0 3 1

Agora verifique que d[] é um potencial relaxado.

Exemplo C.  A tabela abaixo especifica um potencial h[] no grafo da figura. Verifique que o potencial é relaxado. O comprimento do caminho 0-2-7-3-6 é exatamente igual à diferença h[6]-h[0]; portanto, esse caminho é mínimo e a distância de 0 a 6 é 4.

  v  0 1 2 3 4 5 6 7
h[v] 0 2 1 3 1 1 4 2

O comprimento de qualquer caminho de 0 a 1 é pelo menos h[1]-h[0]. Mas todos os caminhos de 0 a 1 têm comprimento maior que h[1]-h[0]. Qual a distância de 0 a 1?

Exemplo D.  A tabela abaixo especifica um potencial h[] no grafo da figura. Verifique que o potencial é relaxado. O caminho 0-4-5-1 é mínimo pois seu comprimento é igual a h[1]-h[0]. O caminho 0-2-7-3 é mínimo pois seu comprimento é igual a h[3]-h[0].

  v  0 1 2 3 4 5 6 7
h[v] 0 3 1 3 1 2 4 2

A diferença h[3]-h[5] mostra que qualquer caminho de 5 a 3 tem comprimento pelo menos 1. Mas a distância de 5 a 3 é maior que 1.

Árvore de caminhos curtos

Para encontrar um caminho mínimo de um vértice s a um vértice t é inevitável calcular todos os caminhos mínimos que começam em s. Isso sugere o seguinte conceito: uma árvore de caminhos curtos de um grafo é uma sub árvore radicada T do grafo tal que

1. todos os vértices do grafo estão em T  (ou seja, T é um sub­grafo gerador) e
2. todo caminho em T a partir da raiz é mínimo no grafo.

Uma árvore de caminhos curtos também é conhecida pela abreviatura SPT de shortest-paths tree. Um grafo tem uma SPT com raiz s  se e somente se  todos os vértices do grafo estão ao alcance de s. Para grafos desse tipo, o problema do caminho mínimo equivale ao seguinte

Mesmo nas instâncias do problema que não têm solução, é claro que existe uma SPT com raiz s no sub­grafo de G induzido pelo conjunto de vértices que estão ao alcance de s.

De acordo com a condição suficiente de minimalidade de caminhos, para resolver o problema da SPT basta encontrar uma árvore radicada geradora T, com raiz s, tal que o vetor das distâncias em T a partir de s seja um potencial relaxado em G.

Exemplo E.  A figura mostra uma sub­árvore radicada T de um grafo G. A raiz da árvore é 5. Veja a lista de todos os caminhos em T que têm origem 5:

5-1-3-6-0
5-1
5-1-3-6-2
5-1-3
5-4
5
5-1-3-6
5-7

Na tabela abaixo, h[v] é o vetor das distâncias em T a partir da raiz. Verifique que h[] é um potencial relaxado em G. Portanto, T é uma SPT de G.

  v   0 1 2 3 4 5 6 7
h[v]  4 1 4 2 1 0 3 1

Caminhos mínimos em dags

Examinaremos a seguir um algoritmo para o problema da SPT restrito a dags, ou seja, a grafos acíclicos. A prova da correção do algoritmo depende da condição suficiente para SPT indicada acima.

Como se sabe, um grafo é acíclico se e somente se tem uma numeração topológica e portanto também uma permutação topológica, digamos vv[0..V-1], dos vértices. O algoritmo processará os vértices em ordem topológica: primeiro vv[0], depois vv[1], depois vv[2], etc.

Ao receber um dag G e um vértice s, o algoritmo deve encontrar uma SPT de G com raiz s. É preciso tomar algumas decisões de projeto: vamos supor que (1) o algoritmo recebe uma permutação topológica vv[] e (2) todos os vértices de G estão ao alcance de s  (e portanto vv[0] ≡ s).

#define Dag Graph

/* A função recebe um dag G,
   uma permutação topológica vv[] dos vértices,
   e um vértice s de G.
   A função supõe que todos os vértices estão ao alcance de s.
   A função armazena em pa[]
   o vetor de pais de uma SPT de G com raiz s.

   As distâncias a partir de s
   são armazenadas no vetor dist[].
   O espaço para os vetores pa[] e dist[]
   deve ser alocado pelo usuário.

   (O código foi inspirado no programa 21.6
   de Sedgewick.) */

void DAGspt( Dag G, vertex *vv, vertex s,
             vertex *pa, int *dist)
{ 
   const int INFINITY = G->V;
   for (vertex v = 0; v < G->V; ++v)
      pa[v] = -1, dist[v] = INFINITY;
   pa[s] = s, dist[s] = 0;

   for (int j = 0; j < G->V; ++j) {
      vertex v = vv[j];
      for (link a = G->adj[v]; a != NULL; a = a->next) {
         vertex w = a->w; 
         if (dist[v] + 1 < dist[w]) {
            dist[w] = dist[v] + 1; // relaxação de v-w
            pa[w] = v;
         }
      }
   }
}

As seguintes observações podem ajudar a entender o código:

• O vetor dist[] é um potencial. A função verifica explicitamente o estado de relaxação de cada arco em relação a esse potencial. Todo arco v-w que estiver tenso é submetido à operação de relaxação dist[w] = dist[v]+1, que diminui dist[w]. O valor de dist[w] pode diminuir várias vezes durante a execução da função.
• A relaxação dos arcos que saem de vv[j] não afeta os vértices vv[0..j-1], que já foram processados, uma vez que todos os vizinhos de vv[j] estão em vv[j+1...].
• A constante INFINITY, igual a G->V, é uma boa representação de ∞ pois seu valor é maior que o comprimento de qualquer caminho em G.

Para verificar que a função está correta, basta observar os seguintes invariantes: no início de cada iteração do processo iterativo principal,

1. o vetor pa[] define uma árvore radicada, digamos T, com raiz s;
2. para todo vértice x de G, dist[x] é a distância de s a x em T ;
3. para todo arco x-y de G, se x está em vv[0..j-1] então x-y está relaxado em relação a dist[].

(Segue imediatamente do invariante 2 que dist[x] vale INFINITY se e somente se x não está em T.)

Agora considere a última iteração, que começa com j ≡ G->V e termina imediatamente. Em virtude do invariante 3, dist[] é um potencial relaxado em G. Em virtude dos invariantes 1 e 2, T é uma árvore radicada em G e dist[] é o vetor das distâncias em T a partir de s. Resta apenas provar que T é geradora de G. Para isso, basta mostrar que não existe arco de G com ponta inicial em T e ponta final fora de T. Tome um arco qualquer x-y de G tal que x pertence a T. Como x-y está relaxado, dist[y] ≤ dist[x] + 1. Graças ao invariante 2, dist[x] < INFINITY. Segue daí que dist[y] < INFINITY e portanto y está em T. Isso mostra que T contém todos os vértices que estão ao alcance de s em G, e portanto todos os vértices de G. Concluímos assim que T satisfaz a condições suficientes para SPT (veja a seção Árvore de caminhos curtos). Portanto T é uma SPT de G.

A função DAGspt() supõe que todos os vértices estão ao alcance de s. Mas não é necessário testar essa condição antes de invocar a função: Se a condição não estiver satisfeita, a função produzirá uma SPT no sub­grafo induzido pelo conjunto de vértices que estão ao alcance de s.

Desempenho.  A função DAGspt() é linear. O consumo de tempo da função é proporcional a  V + A  no pior caso, sendo V o número de vértices e A o número de arcos do dag G. (Se nos restringirmos aos dags em que A ≥ V, podemos dizer que o consumo de tempo é proporcional a A.)  A variante de DAGspt() para dags representados por matriz de adjacências, consome tempo proporcional a V² no pior caso.

Exemplo F.  Considere o dag definido pelos arcos  0-1 1-2 2-4 0-3 3-4. Note que todos os vértices estão ao alcance de 0 e adote a permutação topológica  0 1 2 3 4  dos vértices (faça uma figura). Aplique a função DAGspt() para calcular uma SPT com raiz 0. Veja o estado dos vetores dist[] e pa[] no início de sucessivas iterações (com * representando INFINITY e - representando -1):

          dist[]      pa[]
j vv[j]   0 1 2 3 4   0 1 2 3 4
                               
0   0     0 * * * *   0 - - - - 
1   1     0 1 * 1 *   0 0 - 0 -
2   2     0 1 2 1 *   0 0 1 0 -
3   3     0 1 2 1 3   0 0 1 0 2
4   4     0 1 2 1 2   0 0 1 0 3
5         0 1 2 1 2   0 0 1 0 3

Note que dist[4] começa valendo INFINITY, diminui para 3, e depois para 2. Os valores de pa[4] acompanham essa evolução. No fim, dist[] é o vetor das distâncias a partir de 0 e pa[] representa uma SPT.

Exemplo G.  Considere o dag definidos pelos arcos  0-1 0-2 1-2 0-3 3-4  e adote a permutação topológica  0 1 2 3 4  (faça uma figura). Queremos calcular uma SPT com raiz 1 no subdag induzido pelos vértices que estão ao alcance de 1. Veja o estado dos vetores dist[] e pa[] no início de sucessivas iterações:

          dist[]      pa[]
j vv[j]   0 1 2 3 4   0 1 2 3 4
                               
0   0     * 0 * * *   - 1 - - - 
1   1     * 0 * * *   - 1 - - -
2   2     * 0 1 * *   - 1 1 - -
3   3     * 0 1 * *   - 1 1 - -
4   4     * 0 1 * *   - 1 1 - -
5         * 0 1 * *   - 1 1 - -

No fim da execução de DAGspt(), todos os arcos estão relaxados em relação a dist[]. A árvore radicada definida por pa[] é uma SPT do sub­grafo induzido pelos vértices que estão ao alcance de 1. (Note que não existem arcos com ponta inicial na árvore e ponta final fora da árvore.)