
Valdemar W. Setzer
www.ime.usp.br/~vwsetzer
Original 1/2002; esta versão 1.3 de 24/9/09
5. Um método mais eficiente
Este capítulo é diferente do correspondente no artigo original, pois em lugar de ilustrar um método mais eficiente usando a ordenação por árvore (tree sort) usa um outro método, ordenação por intercalação binária (binary merge sort). A sugestão do uso desse outro método, muito mais simples e ilustrativo, e até um pouco mais eficiente, foi feita pelo Prof. Michael Schrefl, da Johannes Keppler Universität de Linz, Áustria, a quem muito agradecemos. Acione aqui para o artigo com o capítulo original.
5.1 Motivação
O instrutor relata que seu chefe provavelmente dirá: "Seus amigos levaram de 30 a 40 minutos para achar essas soluções. Será que se eles ficassem uma manhã inteira trabalhando obteriam algo melhor?" Pergunta aos participantes o que eles acham. Em geral, a maioria acha que é possível obter algo melhor, mas sempre há os que pensam não ser possível.
Um método muito mais eficiente, ordenação por intercalação binária (binary merge sort), é então introduzido. Vamos apresentá-lo aqui de uma forma em que pelo menos uma parte dos estudantes podem participar do processo, fazendo algo com seus corpos e mãos, assim ilustrando de maneira viva o processo para o resto da classe. No item 5.6 mostramos duas variações, sendo que em uma delas pode-se ter uma situação semelhante à dos outros métodos já vistos, isto é, uso de cartolinas.
5.2. Preparação
Chama-se um estudante qualquer , que deve ficar à frente do quadro negro, voltado para a classe, mais ou menos na altura do meio da parede do quadro. Dá-se a esse estudante um maço com os 8 cartões com os números, embaralhados. Agora diz-se à classe que esse estudante é muito preguiçoso para ordenar todos os cartões. Assim, ele precisa de 2 ajudantes. O aluno deve escolher esses 2 ajudantes dentre seus colegas. O instrutor posiciona esses 2, olhando para a classe, à frente do primeiro, formando uma nova fileira (a segunda, considerando-se que o primeiro estudante forma uma fileira por si só), de modo que cada um deles divida, em duas partes mais ou menos iguais, cada metade da largura da classe (distância entre as paredes do lado), conforme a fig. 4.

fig. 4
O primeiro estudante, sendo preguiçoso, passa a tarefa de ordenar seu maço a seus 2 colegas, distribuindo para isso seus cartões igualmente entre eles, isto é, um maço de 4 cartões para cada um. A seguir, espera que cada um ordene o maço que recebeu. Acontece que esses 2 estudantes também são preguiçosos, de modo que cada um vai, por sua vez, chamar 2 ajudantes. Esses 4 são posicionados em uma terceira fileira à frente dos que os chamaram, cada um dividindo mais ou menos 1/4 da largura da sala em dois, conforme a fig. 5.
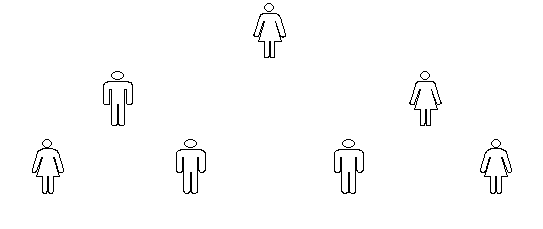
fig. 5
Em seguida, cada um dos ajudantes do primeiro divide seu maço de cartões igualmente entre seus ajudantes, cada um deles recebendo 2 cartões. Esses também são preguiçosos, de modo que chamam, cada um, dois ajudantes, formando uma quarta fileira com 8. Cada estudante da terceira fileira distribui seus dois cartões para cada um de seus ajudantes, isto é, um cartão para cada um. Na fig. 6 mostramos essa situação, colocando os valores dos cartões na posição de cada estudante da última fileira.
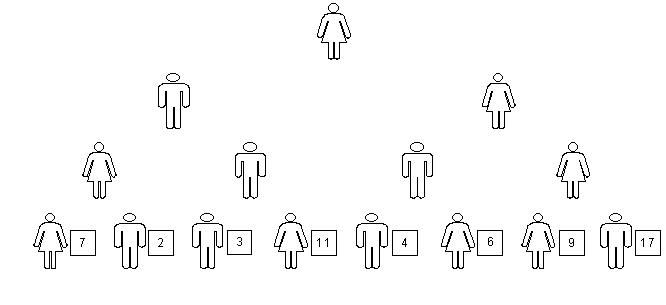
fig. 6
O instrutor desenha no quadro negro essa figura, incluindo o valor dos cartões da última fileira. Ele diz que essa estrutura, muito usada em computação, é denominada de árvore, aqui uma "árvore de pessoas"; diz, por exemplo, que como os "computatas" parecem andar e falar com a cabeça virada, desenham suas árvores "de cabeça para baixo". Anota no quadro as denominações usuais: cada fileira é denominada de nível da árvore; cada elemento da árvore é um nó da árvore; cada nó do último nível (com 8 estudantes) é uma folha da árvore; o nó do primeiro nível (com um único estudante) é a raiz da árvore; cada nó fora da raiz tem um único nó pai, no nível anterior, e cada nó fora das folhas tem exatamente dois nós filhos na fileira seguinte, o que caracteriza essa estrutura de dados como uma árvore binária. A altura da árvore é o número de níveis da mesmo, isto é, o número de nós que se pode percorrer desde a raiz até uma folha, sempre no sentido dos filhos (no exemplo, a altura é 4).
É importante mostrar que a regra de formação da árvore é uniforme: cada nó constrói a parte da árvore correspondente a seus 2 filhos, e passa metade de seu maço a cada um. Isso acontece com todos os níveis intermediários, a menos do nível dos nós folhas que, por terem recebido apenas um cartão, não podem mais dividir seu maço (unitário) em 2, o que assinala o fim da construção da árvore.
5.3 Ordenação
Construída a árvore, passa-se à fase de ordenação. Cada estudante da penúltima (terceira) fileira, um de cada vez, da esquerda da sala para a direita, vira seus ajudantes para si, e examina seus cartões, pegando em primeiro lugar o cartão de menor valor (ou a que está à sua direita, se tiverem o mesmo valor), mantendo-a com a face para cima, e depois a de maior valor (ou a outra, se tiverem o mesmo valor), colocando esta por baixo da anterior, também com a face para cima. A seguir, vira seus ajudantes novamente para a classe, e mostra a esta os cartões um pouco deslocados para se poder ver seu valor. O instrutor copia esses valores no nó correspondente na árvore do quadro negro. Quando todos os estudantes da terceira fileira tiverem feito isso, teremos 4 maços ordenados de 2 cartões cada, como na fig. 7.
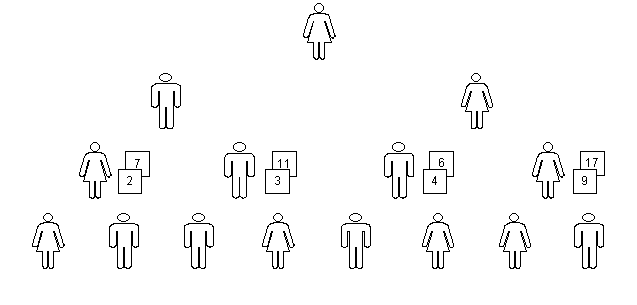
fig. 7
Cada estudante da segunda fileira vira seus ajudantes para si e pega, um por um, os cartões de seus ajudantes, intercalando-os em ordem crescente de valor (ou em ordem não decrescente, se houver cartões com mesmo valor). Para isso, examina de cada vez os cartões superiores dos maços de seus ajudantes e pega o de menor valor, colocando-o em baixo do cartão que já pegou anteriormente, se houver. Seria interessante ele contar à classe quais cartões estão na parte superior dos maços de seus ajudantes. Quando um cartão é retirado de um ajudante, aparece o cartão seguinte, para posterior comparação, até que acabem todos os seus cartões. O instrutor deve notar para a classe que, para cada estudante da segunda fileira, o último cartão que sobrar não é comparada, pois o seu outro ajudante já não tem nenhum cartão, podendo ser movida para baixo do maço. Após o último cartão, os ajudantes são voltados novamente para a classe e o maço resultante é mostrado para a classe; o instrutor copia os valores no nó correspondente no quadro-negro. Quando não sobrar mais nenhum cartão na terceira fileira, cada um dos dois estudantes da segunda fileira tem um maço de 4 cartões, ordenados em ordem crescente, como na fig. 8.
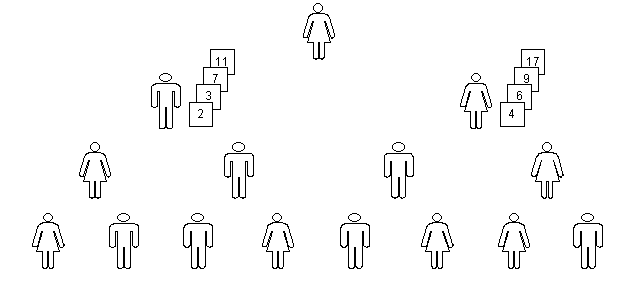
fig. 8
O estudante da primeira fila (o do nó raiz) vira seus ajudantes para si, e começa a retirar os seus cartões, intercalando-os do mesmo modo como os da segunda fileira retiraram os cartões de seus ajudantes da terceira. O instrutor nota novamente que o último cartão que sobrar com um dos ajudantes não é comparada, sendo simplesmente movida para baixo do maço que está com o estudante da raiz. Os ajudantes voltam-se para a classe. Ao fim desse processo, o estudante da raiz tem um maço de cartões ordenados em ordem crescente, que mostra deslocados para a classe; o instrutor copia-os no quadro-negro, no nó raiz da árvore, como na fig. 9.
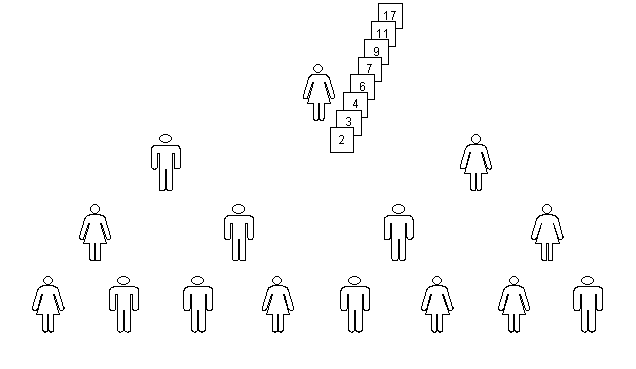
fig. 9
Novamente, é importante o instrutor chamar a atenção para a uniformidade do processo: cada estudante intercala os cartões de seus dois ajudantes; no caso dos estudantes da terceira fileira, também há um processo de intercalação, reduzido a um caso trivial, pois cada um de seus ajudantes tem apenas um cartão. Nesse caso há uma só comparação, seguindo-se o movimento do cartão de menor valor e finalmente um simples movimento do último cartão como nos nós intermediários. O processo de ordenação termina quando o estudante do nó raiz tiver terminado a intercalação dos maços de seus ajudantes.
O instrutor pede aos alunos da árvore para sentarem, e passa a usar apenas o quadro-negro nas explicações seguintes, tentando sempre lembrar aos estudantes o que se passava na árvore real. Uma outra possibilidade é enviar os estudantes de cada fileira para suas carteiras, assim que não houver mais cartões na fileira. Dessa maneira, o processo de intercalação fica mais visível.
5.4 Cálculo da complexidade
No cálculo de quantas comparações são necessárias para ordenar n números com esse método, vamos ignorar a construção da árvore, pois ela não requer nenhuma comparação e, como veremos em 5.6, nem mesmo é necessária. Passemos, portanto, à fase de ordenação.
Recordemos que, para cada estudante de uma fileira, cada cartão que ele retira de um ajudante e coloca em seu maço é comparado com o cartão de cima do maço do outro ajudante, a menos do último cartão que, como salientamos acima, é colocado sem comparação no fim do seu maço (já que acabou o maço do outro ajudante). O instrutor chama a atenção para o fato de esse ser o pior caso, já que pode acontecer de um dos ajudantes ficar sem cartões e o outro ainda ter 2 ou mais cartões, caso em que haverá 2 ou mais comparações a menos; é interessante dar um exemplo, como o caso extremo de os maços conterem 1-2-3-4 e 5-6-7-8 respectivamente, em que haverá 4 comparações (por construção, cada maço está ordenado, de modo que ao acabar o primeiro maço, basta ir retirando cada cartão do outro, consecutivamente), em lugar de 7 que seria o pior caso. Portanto, no pior caso, considerando-se todos os estudantes de uma fileira, o número de comparações é o número total de cartões n menos o número de estudantes da fileira (pois haverá, por estudante, uma comparação a menos do que o número total de cartões nos dois maços de seus ajudantes).
O instrutor constrói no quadro negro, ao lado da árvore do exemplo, uma tabela cujas linhas devem ficar em paralelo com os níveis da árvore, acrescida das 3 linhas como abaixo. A segunda coluna indica quantos nós existem em cada nível, e a terceira quantas comparações serão feitas em cada nível. A generalização das 3 últimas linhas deve ser bem esclarecida.
|
Nível |
Nós |
Compar. |
|
0 |
1 |
n-1 |
|
1 |
2 |
n-2 |
|
2 |
4 |
n-4 |
|
3 |
8 |
n-8 |
|
... |
... |
... |
|
m-1 |
2m-1 |
n-n/2 |
|
m |
2m |
n-n=0 |
Portanto, o número total de comparações C é dado pela soma de todos os termos da última coluna, menos o da última linha, isto é, até a linha m-1 inclusive:
C = (n-1) + (n-2) + (n-4) + (n-8) + ... + (n-n/2)
Como são m termos a serem somados (contagem de 0 a m-1, na coluna da esquerda),
C = mn - (1 + 2 + 4 + 8 + ... + n/2)
O instrutor observa que o segundo termo dessa última fórmula indica o número total de nós de uma árvore binária em que o número de folhas é n/2. Mostrando vários níveis da árvore do quadro negro, ele observa que, se um nível qualquer tem k nós, o número total de nós desde a raiz até esse nível é sempre 2k-1. (Isso pode ser facilmente provado por indução finita no número de níveis m, mas se os alunos não conhecem provas por indução, isso seria demais.) Assim,
C = mn - [2(n/2) - 1]
Resta calcular o m, que indica o nível das folhas. Ora, por construção, o número de nós no nível das folhas é o número n de valores que queremos ordenar. Observando a tabela, temos
2m = n
podendo-se ver isso na árvore do exemplo (para m=3, 2m=23=8). Tirando o logaritmo na base 2 de ambos os lados,
log22m = log2n
m log22 = log2n
m = log2n
É interessante observar que essa fórmula permite o cálculo da altura m+1 de uma árvore binária dado o número de folhas n.
Portanto, o número total de comparações no pior caso será
C = nlog2n - n + 1
É importante observar que essa fórmula vale para n igual a uma potência de 2. Se n não é uma potência de 2, pode-se sempre completar as folhas que estariam vazias colocando nelas um número maior do que qualquer valor a ser ordenado (fazendo o papel de infinito), e depois da ordenação retirar os cartões que o contenham, e que no fim estarão abaixo do cartão com o maior valor a ser ordenado. Assim, se 2m-1<n<2m, deve-se tomar m para o cálculo do número de comparações.
5.5 Comparação com os métodos quadráticos
A tabela abaixo mostra o número de comparações nos piores casos dos métodos quadráticos e do método por intercalação binária:
|
n |
n(n-1)/2 |
nlog2n - n + 1 |
|
1 |
0 |
0 |
|
2 |
1 |
1 |
|
4 |
6 |
5 |
|
8 |
28 |
17 |
|
16 |
120 |
49 |
|
32 |
496 |
129 |
|
64 |
2.016 |
321 |
|
128 |
8.028 |
769 |
|
256 |
32.640 |
1.793 |
|
512 |
130.816 |
4.097 |
|
1024 |
523.776 |
9.217 |
|
2048 |
2.096.128 |
20.481 |
|
4096 |
8.386.560 |
45.057 |
|
8192 |
33.550.336 |
98.305 |
Seria interessante o instrutor chamar a atenção para o fato de que no método quadrático, assintoticamente tem-se n2 comparações (representado como O(n2), lido "da ordem de n2"), isto é, como o número de elementos dobra em cada nova linha, o número de comparações praticamente quadruplica. No método de intercalação tem-se assintoticamente nlog2n (representado como O(nlog2n)); como o logaritmo é uma função que tende a aumentar pouco com o aumento de seu argumento, a tendência é de o número de comparações dobrar ao dobrar-se o número de valores a serem ordenados.
O instrutor deve também chamar a atenção para a diferença brutal de eficiência entre os métodos. Um exemplo real interessante é o de listas telefônicas, que devem ser sempre ordenadas para cada nova edição, supondo-se que os novos assinantes sejam colocados inicialmente no fim da lista anterior. Para uma lista com 131.072 assinantes, temos 8.589.869.056 e 2.097.153 comparações para os dois métodos, respectivamente. Já para 1.048.576 assinantes, temos 549.755.813.888 e 19.922.945 comparações. Em um computador que faz 1.000.000 comparações por segundo, temos nesse último caso um tempo de execução dos programas (só nas comparações!), aproximadamente de 6 dias e de 19 segundos, nos piores casos, respectivamente.
Uma comparação interessante é que os métodos quadráticos não necessitavam de "espaço auxiliar", isto é, compartimentos intermediários adicionais. No caso do método por intercalação binária, como apresentado, é necessário usar n-1 nós (estudantes) auxiliares, que é o número de nós da árvore sem contar as folhas.
5.6 Possíveis variações
Em lugar de se construir a árvore da maneira vista, isto é, dando o maço inicial embaralhado para o estudante da raiz, e prosseguindo como descrito, pode-se construir a árvore sem os maços de cartões. Em seguida, pode-se distribuir os cartões embaralhados pelos estudantes das folhas da árvore. Prossegue-se com o item 5.3.
Uma outra possibilidade é de se construir apenas as folhas da árvore, distribuindo-se os cartões pelos estudantes dessa fileira. A seguir, constrói-se a próxima fileira, procedendo-se às intercalações dos cartões das folhas, depois constrói-se mais uma fileira, seguida das correspondentes intercalações, e assim por diante. Em outras palavras, os nós são construídos apenas quando necessários.
Em lugar de se construir uma árvore, pode-se usar apenas duas fileiras A e B de 8 estudantes cada, voltados face a face. Como exemplo, para o caso de 8 cartões vamos denominar os estudantes de A de A1 a A8, os de B de B1 a B8, de tal modo que A1 está em frente de B1, etc. A idéia é fazer a intercalação dos cartões de dois grupos de estudantes que estão na fileira A (ou B) movendo-os para o grupo paralelo de estudantes da outra fileira B (ou A), sempre um cartão por estudante. Em cada passo dobra-se o número de estudantes de cada grupo. No início, a intercalação é feita entre 2 grupos de um estudante cada (entre A1 e A2, entre A3 e A4, etc., com os cartões intercalados movidos para B1 e B2, B3 e B4, etc., respectivamente), depois com 2 grupos de 2 estudantes cada (entre B1, B2 e B3, B4, entre B5, B6 e B7,B8), e finalmente entre 2 grupos de 4 estudantes (entre A1 a A4 e A5 a A8). Para isso, pode-se usar um estudante que executa as comparações e os movimentos dos cartões; pode-se também usar estudantes que funcionam como "ponteiros", 2 deles indicando com o dedo quais elementos de cada grupo devem ser comparados, digamos na fileira A, e mais um indicando para qual estudante da outra fileira, no caso a B, o próximo cartão deve ser movido.
Nesse segundo método, é necessário usar um espaço de armazenamento auxiliar com n elementos. Ele pode ser feito com cartolinas, com duas filas de compartimentos, em lugar de usar os estudantes. Isso dá a oportunidade de todos os estudantes da classe participarem, como nos métodos quadráticos. Ao usar-se cartolinas, é interessante acrescentar uma regra adicional às R1 a R5 já vistas nos métodos quadráticos:
R6. Permite-se o uso de mais compartimentos auxiliares.
Uma pequena modificação desse último método pode ser sugerida: de fato, só é necessário usar n/2 compartimentos auxiliares de armazenamento. Quando se intercalam os nós-folha (nível m, com grupos de 1 nó), construindo-se o nível m-1, é eventualmente necessário trocar de posição 2 cartões de compartimentos consecutivos, de modo que nenhum compartimento auxiliar é realmente necessário. Para o passo correspondente à construção do nível m-2 (grupos de 2), é necessário usar apenas 4 compartimentos auxiliares. O resultado da intercalação de cada par de grupos é movido para os compartimentos originais. Ao intercalarem-se os nós correspondentes ao nível 2 (grupos de n/4), é necessário usar apenas n/2 compartimentos auxiliares, com o resultado da intercalação de cada par de grupos sendo movido, como nos outros passos, nos compartimentos originais. A última intercalação, correspondendo aos elementos do nível 1, é feita usando apenas os compartimentos originais.
É possível fazer uma ordenação por intercalação binária usando apenas os n espaços originais, isto é, sem um número variável de compartimentos adicionais, o que é denominado de in-place merge. Descrevemos um algoritmo simples que usa mais comparações. Suponhamos que se estejam intercalando dois grupos de elementos G e H, já ordenados. Se o elemento examinado de G for maior do que o elemento examinado de H, deve-se trocá-los. O novo elemento de G deve ser necessariamente menor do que os restantes desse grupo, mas o mesmo não se passa com o novo elemento de H. Nesse caso, ele deve ser deslocado até sua posição correta, a fim de não quebrar a ordenação de H. Por exemplo, suponhamos que no caso de 8 valores a serem ordenados tenha-se chegado aos seguintes dois grupos de 4 elementos:
1-3-6-7#2-4-5-8
Os passos seguintes seriam:
1-2-6-7#3-4-5-8; 1-2-3-7#6-4-5-8; 1-2-3-7#4-6-5-8; 1-2-3-7#4-5-6-8; 1-2-3-4#7-5-6-8; 1-2-3-4#5-7-6-8; 1-2-3-4#5-6-7-8
É fácil verificar que se houver dois grupos de k elementos para serem intercalados, no pior caso haverá 2k-1 comparações para as intercalações (como já visto), mais k(k-1) para os deslocamentos (por exemplo, no caso extremo dos grupos 5-6-7-8#1-2-3-4). Esse segundo termo torna o método quadrático - na verdade, da ordem de O(n2log2n).
O instrutor pode ainda acrescentar que existem métodos, como Quicksort, de ordem O(nlog2n) (ver, por exemplo, [2], no artigo original), que não é um método por intercalação, que não necessitam de espaço auxiliar variável (na verdade, o Quicksort necessita de espaço adicional variável para guardar a pilha da recursão ou, se a recursão é eliminada, uma pilha substituindo a chamada recursiva que não é do tipo tail recursion; o espaço adicional da pilha é da ordem de log2n [2]).