1. Introdução
Algoritmos existem desde a remota antigüidade. A execução de uma soma armada de 2 números com vários algarismos segue um algoritmo; o famoso "algoritmo de Euclides" para cálculo de máximo divisor comum, se o autor assumido foi seu inventor, data do 3o século a.C.
Hoje em dia a noção e domínio dos algoritmos tornou-se absolutamente essencial, pois qualquer programa de computador que "funciona", isto é, dá os resultados esperados, deve ser provavelmente uma descrição de um algoritmo. (Se o leitor estranhou esse "provavelmente", provavelmente necessita entender melhor o que é um algoritmo e um programa…) Mais, se se deseja elaborar um programa para um computador, a maneira correta de fazê-lo seria inicialmente procurar os métodos mais adequados à solução do problema em questão, especificar essa solução como um algoritmo e, depois disso, formulá-lo em alguma linguagem de programação para poder introduzi-lo no computador.
Do ponto de vista educacional, parece-nos essencial que se ensine que "programar um computador" não é colocar na máquina alguns comandos expressos na sintaxe de uma linguagem de programação, modificá-los e rearranjá-los até que se obtenha algum resultado esperado, como se fosse um joguinho eletrônico. A essência da programação e da computação, aquilo que realmente deveria atrair o interesse dos jovens pela área, é a elaboração e análise de algoritmos.
Neste artigo expomos uma atividade de ensino da noção de algoritmo e de sua análise de complexidade, adequada para a última série do ensino médio ou para cursos universitários. Esta atividade foi desenvolvida pelo segundo autor como parte de um programa de divulgação do curso de Ciência da Computação do IME-USP, tendo já sido aplicada inúmeras vezes com bastante sucesso. Sua duração é de aproximadamente 3 horas, não exigindo experiência prévia por parte dos alunos. Emprega material didático físico, apresentando um problema com números sob forma de um jogo manual competitivo. Os alunos resolvem o problema em grupos, tendo uma razoável margem de manobra para exercer sua criatividade, e comparam, em seguida, as diferentes soluções obtidas. Posteriormente, é feita pelo instrutor uma abstração dos conceitos envolvidos na resolução do problema proposto, e é apresentada uma solução muito mais complexa, mas mais eficiente. São então apresentados conceitos avançados como "corretude", e complexidade de algoritmos, a noção de algoritmo ótimo e a intratabilidade de certos problemas. Tudo isso é feito desvinculado do computador, de modo que nem é necessário ter-se a disponibilidade dessa máquina para introduzir noções conceituais sobre computação e programação. Por outro lado, se existe disponibilidade educacional de tal máquina, nosso método pode servir de introdução à programação prática.
2. O problema proposto
Escolhemos, para introduzir as noções desejadas, o problema de ordenar n números.
2.1 Enunciado
Como recurso didático, o instrutor conta aos alunos que seu chefe passou-lhe o seguinte problema:
"Aqui está uma cartolina com compartimentos, numerados de 1 a 8 (fig. 1). Dentro de cada compartimento está uma tira de cartolina com um número natural nela escrito. O chefe pediu-me que rearranjasse as tiras de forma a ficarem em ordem crescente dos números nelas escritos, com as seguintes regras:
R1. É possível levantar um pouco uma tira de seu compartimento, a fim de examinar seu conteúdo, isto é, o número nela inscrito.

fig. 1
R2. Se uma tira estiver abaixada, isto é, seu número está invisível, este é considerado desconhecido. O operador não pode memorizar os conteúdos dos compartimentos.
R3. No máximo 2 tira podem estar levantadas ao mesmo tempo (fig. 2).

fig. 2
R4. Os conteúdos de 2 tiras levantadas podem ser comparados, determinado-se qual tira possui o menor número.
R5. Duas tiras podem ser trocadas de compartimento (fig. 3 em relação à fig. 2).

fig. 3
Vou aproveitar que vocês estão aqui para que me ajudem (faz de conta que não consegui resolver o problema), em grupos de até 3 participantes. Vamos ver quais serão os três grupos que primeiro resolvem o problema; estes ganharão, como magnífico brinde, as cartolinas que usaram, com as respectivas tiras."
2.2 Considerações práticas
Temos utilizado uma cartolina branca de aproximadamente 80 cm por 25 cm; os compartimentos são pedaços de cartolina colorida de 9 cm por 9 cm, com a parte inferior grampeada e os lados direito e esquerdo colados. As tiras são pedaços de cartolina de outra cor de 5 cm por 12 cm, com os números (até 3 algarismos) escritos na metade inferior. A cartolina branca pode ser dobrada ao meio para facilitar o transporte e o armazenamento.
Uma outra possibilidade, menos ilustrativa mas bem mais simples, é usar apenas as tiras, que podem ser 8 pedaços de qualquer papel de mesmo tamanho e cor, colocados em linha sobre a carteira, com os números para baixo. No restante deste artigo, usaremos a descrição com a cartolina.
O instrutor enuncia o problema, distribui um papel com as regras, explica-as usando uma cartolina e, em seguida, distribui uma cartolina para cada grupo. Em geral leva de 10 a 15 minutos para os 3 primeiros grupos resolverem o problema.
3. Soluções obtidas
3.1 Descrição e generalização das soluções
O instrutor conta aos participantes que seu chefe dar-lhe-á mais dessas tarefas podendo haver cartolinas com um número qualquer de compartimentos. Ele solicita então aos participantes de cada grupo vencedor que o ajudem, descrevendo o método que usaram, a fim de que ele possa aprendê-lo. Pede também que o generalizem para um número qualquer dado, n, de compartimentos. Pede aos outros que permaneçam em silêncio, prestando atenção para ver se sua solução foi a mesma ou se foi deferente. O instrutor precisa ajudar os grupos a descrever de uma maneira razoavelmente lógica o processo que imaginaram. Depois das descrições dos grupos vencedores, o instrutor pergunta se algum outro grupo teve alguma idéia diferente, e pede que a descreva.
3.2 Tipos de soluções
Em geral, os participantes chegam às 3 soluções mais simples e tradicionais para o problema de ordenação, descritas em qualquer livro introdutório sobre algoritmos [1]. Quando dois grupos vencedores chegarem a uma mesma solução, em geral algum grupo não vencedor chegou à solução restante.
O instrutor mostra que os 3 métodos são descritos na literatura, exibindo os capítulos correspondentes nos livros. Isso deixa os participantes muito impressionados, pois tomam consciência de sua capacidade de inventar processos mencionados internacionalmente. Pergunta-se-lhes o nome que dariam aos métodos e apresentam-se os nomes tradicionais usados na literatura. São distribuídas folhas mostrando cada um dos métodos com um exemplo. Para orientação dos leitores que não são da área de Ciência da Computação, apresentamos a seguir esses métodos; as folhas distribuídas contêm exatamente os mesmos dizeres de cada item abaixo. Note-se a evolução na formalização dos algoritmos. A versão 1 mostra a solução como é dada em geral pelos participantes; nas versões seguintes vai-se aproximando cada vez mais de um algoritmo formal. Depois desses itens fazemos algumas observações práticas.
3.2.1 O método de seleção
Chamemos os conteúdos de n compartimentos de C1, …,Cn.
Versão 1 (descrição informal). Compare C1 com C2 troque-os de compartimento se C1 > C2. Faça o mesmo com C1 e C3, depois com C1 and C4, etc., até C1 e Cn. Com isso, no fim dessa fase o menor elemento da seqüência estará no compartimento 1. Fazemos agora uma segunda fase, comparando C2 com C3, trocando-os se C2 > C3, e fazendo o mesmo com C2 e C4, C2 e C5, ..., C2 e Cn. Com isso o compartimento 2 ficará com o segundo menor elemento da seqüência. Repetimos essas fases iniciando com C3, depois com C4, … até iniciar com Cn-1. As tiras ficarão ordenadas como desejado.
Versão 2 (formalização inicial)
para i variando de 1 até n-1
faça: compare Ci com Ci+1, Ci com Ci+2, ... , até Ci com Cn, trocando cada par de seu compartimentos se Ci > Ci+j.
Versão 3 (formalização final)
para i variando de 1 até n-1
faça: para j variando de i+1 até n
faça: se Ci > Cj troque-os de compartimentos
Exemplo (a tabela mostra a situação após a execução do passo indicado pelos valores de i e de j:
|
i |
j |
compartimentos: |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
|
valores iniciais: |
5 |
10 |
3 |
7 |
15 |
2 |
1 |
9 |
|
1 |
2 |
|
5 |
10 |
3 |
7 |
15 |
2 |
1 |
9 |
|
|
3 |
|
3 |
10 |
5 |
7 |
15 |
2 |
1 |
9 |
|
... |
||||||||||
|
|
6 |
|
2 |
10 |
5 |
7 |
15 |
3 |
1 |
9 |
|
|
7 |
|
1 |
10 |
5 |
7 |
15 |
3 |
2 |
9 |
|
|
8 |
|
1 |
10 |
5 |
7 |
15 |
3 |
2 |
9 |
|
2 |
3 |
|
1 |
5 |
10 |
7 |
15 |
3 |
2 |
9 |
|
... |
||||||||||
|
|
8 |
|
1 |
2 |
10 |
7 |
15 |
5 |
3 |
9 |
|
3 |
4 |
|
1 |
2 |
7 |
10 |
15 |
5 |
3 |
9 |
|
... |
||||||||||
|
|
8 |
|
1 |
2 |
3 |
10 |
15 |
7 |
5 |
9 |
|
4 |
5 |
|
1 |
2 |
3 |
10 |
15 |
7 |
5 |
9 |
|
... |
||||||||||
|
|
8 |
|
1 |
2 |
3 |
5 |
15 |
10 |
7 |
9 |
|
5 |
6 |
|
1 |
2 |
3 |
5 |
10 |
15 |
7 |
9 |
|
... |
||||||||||
|
|
8 |
|
1 |
2 |
3 |
5 |
7 |
15 |
10 |
9 |
|
6 |
7 |
|
1 |
2 |
3 |
5 |
7 |
10 |
15 |
9 |
|
|
8 |
|
1 |
2 |
3 |
5 |
7 |
9 |
15 |
10 |
|
7 |
8 |
|
1 |
2 |
3 |
5 |
7 |
9 |
10 |
15 |
3.2.2 O método da bolha
Versão 1 (descrição informal). Compare C1 com C2 e troque-os de compartimentos se C1 > C2. Faça o mesmo com C2 e C3, depois C3 e C4, até Cn-1 e Cn. Com isso, no fim dessa fase o maior elemento da seqüência estará no compartimento n. Fazemos agora uma segunda fase, indo com as comparações até Cn-1, e então teremos o segundo maior elemento da seqüência no compartimento n - 1. Repetimos essas fases indo com as comparações até Cn-2, depois Cn-3, … e, por último, indo até C2. As tiras terminam ordenadas.
Versão 2 (formalização inicial)
para i variando de n até 2
faça: compare C1 com C2, C2 com C3, … , até to Ci-1 com Ci, trocando cada par de seus compartimentos se Cj > Cj+1
Versão 3 (formalização final)
for i varying from n down to 2
faça: para j variando de 1 até i-1
faça: se Cj > Cj+1, troque-os de compartimentos
|
i |
j |
compartimentos: |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
valores iniciais: |
5 |
10 |
3 |
7 |
15 |
2 |
1 |
9 |
||
|
8 |
1 |
5 |
10 |
3 |
7 |
15 |
2 |
1 |
9 |
|
|
2 |
5 |
3 |
10 |
7 |
15 |
2 |
1 |
9 |
||
|
3 |
5 |
3 |
7 |
10 |
15 |
2 |
1 |
9 |
||
|
4 |
5 |
3 |
7 |
10 |
15 |
2 |
1 |
9 |
||
|
5 |
5 |
3 |
7 |
10 |
2 |
15 |
1 |
9 |
||
|
6 |
5 |
3 |
7 |
10 |
2 |
1 |
15 |
9 |
||
|
7 |
5 |
3 |
7 |
10 |
2 |
1 |
9 |
15 |
||
|
7 |
1 |
3 |
5 |
7 |
10 |
2 |
1 |
9 |
15 |
|
|
... |
||||||||||
|
6 |
3 |
5 |
7 |
2 |
1 |
9 |
10 |
15 |
||
|
6 |
1 |
3 |
5 |
7 |
2 |
1 |
9 |
10 |
15 |
|
|
... |
||||||||||
|
5 |
3 |
5 |
2 |
1 |
7 |
9 |
10 |
15 |
||
|
5 |
1 |
3 |
5 |
2 |
1 |
7 |
9 |
10 |
15 |
|
|
... |
||||||||||
|
4 |
3 |
2 |
1 |
5 |
7 |
9 |
10 |
15 |
||
|
4 |
1 |
2 |
3 |
1 |
5 |
7 |
9 |
10 |
15 |
|
|
... |
||||||||||
|
3 |
2 |
1 |
3 |
5 |
7 |
9 |
10 |
15 |
||
|
3 |
1 |
1 |
2 |
3 |
5 |
7 |
9 |
10 |
15 |
|
|
2 |
1 |
2 |
3 |
5 |
7 |
9 |
10 |
15 |
||
|
2 |
1 |
1 |
2 |
3 |
5 |
7 |
9 |
10 |
15 |
3.2.3 O método da inserção
- Versão 1 (descrição informal). Em uma fase inicial, compare C2 com C1 and troque-os de compartimentos se C2 < C1. Com isso garantimos que a seqüência C1 a C2 está em ordem crescente. Numa segunda fase, compare C3 com C2, trocando-os de compartimentos se C3 < C2. Se houve troca, compare C2 com C1, trocando-os de compartimentos se C2 < C1. Após essa segunda fase temos a garantia de que C1 até C3 estão ordenados. Repetimos essas fases começando com C4, C5, … até Cn. A última fase (que começa com Cn) fica assim: compare Cn com Cn-1 e troque-os de compartimentos se Cn < Cn-1; se houve troca, compare Cn-1 com Cn-2 e troque-os de compartimentos se Cn-1 < Cn-2; repita esse processo até não ser necessária a troca de compartimentos ou até chegar na comparação e eventual troca de C2 com C1.
Versão 2 (formalização inicial)
para i variando de 2 até n
faça: compare sucessivamente os elementos dos pares
(Cj , Cj-1) para j de i até
2 or encontrar Cj > Cj-1;
para cada
par dessa coleção, troque Cj com Cj-1
se Cj < Cj-1
Versão 3 (formalização final)
para i variando de 2 até n
faça: j ← i;
enquanto (Cj
< Cj-1) e (j > 1)
faça:
troque Cj and Cj-1; j ← j-1
|
i |
j |
compartimento: |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
valor inicial: |
5 |
10 |
3 |
7 |
15 |
2 |
1 |
9 |
||
|
2 |
2 |
|||||||||
|
3 |
3 |
5 |
3 |
10 |
7 |
15 |
2 |
1 |
9 |
|
|
2 |
3 |
5 |
10 |
7 |
15 |
2 |
1 |
9 |
||
|
4 |
4 |
3 |
5 |
7 |
10 |
15 |
2 |
1 |
9 |
|
|
3 |
||||||||||
|
5 |
5 |
|||||||||
|
6 |
6 |
3 |
5 |
7 |
10 |
2 |
15 |
1 |
9 |
|
|
5 |
3 |
5 |
7 |
2 |
10 |
15 |
1 |
9 |
||
|
4 |
3 |
5 |
2 |
7 |
10 |
15 |
1 |
9 |
||
|
3 |
3 |
2 |
5 |
7 |
10 |
15 |
1 |
9 |
||
|
2 |
2 |
3 |
5 |
7 |
10 |
15 |
1 |
9 |
||
|
7 |
7 |
2 |
3 |
5 |
7 |
10 |
1 |
15 |
9 |
|
|
6 |
2 |
3 |
5 |
7 |
1 |
10 |
15 |
9 |
||
|
5 |
2 |
3 |
5 |
1 |
7 |
10 |
15 |
9 |
||
|
4 |
2 |
3 |
1 |
5 |
7 |
10 |
15 |
9 |
||
|
3 |
2 |
1 |
3 |
5 |
7 |
10 |
15 |
9 |
||
|
2 |
1 |
2 |
3 |
5 |
7 |
10 |
15 |
9 |
||
|
8 |
8 |
1 |
2 |
3 |
5 |
7 |
10 |
9 |
15 |
|
|
7 |
1 |
2 |
3 |
5 |
7 |
9 |
10 |
15 |
||
|
6 |
3.3 Observações práticas
Uma variação do método de seleção abordada em seguida pelo instrutor e já sugerida uma vez por um grupo, é de se efetuar uma única troca em cada varrida de comparações de i a n; para isso, pode-se simplesmente deixar levantada a tira do compartimento com o menor número encontrado de i a j, i ≤ j ≤ n; achando-se uma posterior menor, levanta-se a tira e abaixa-se a primeira; a menor é finalmente trocada com a i-ésima. Apesar de se manter o número de comparações, a troca única diminui o número de operações, o que já começa a introduzir a noção de eficiência.
Um aperfeiçoamento do método da bolha, muitas vezes indicado pelos alunos, é o de parar a execução do algoritmo logo após uma fase em que não haja nenhuma troca, pois então a seqüência já estará ordenada.
4. Análise das soluções
O instrutor continua contando o drama de sua vida: ao apresentar as diversas soluções ao chefe, este certamente perguntar-lhe-á qual delas é a melhor. Espera-se a manifestação dos participantes, orientando-os com questões como: "o que significa ser a melhor?"; "como comparar as eficiências?"; "quais das operações que vocês fizeram deram trabalho para ser efetuadas?".
O instrutor acaba por sugerir (ou confirmar alguma sugestão vinda dos participantes) que uma boa medida é contar em cada caso o número de comparações e de trocas.
Analisando-se os três métodos, pode-se ver que no de seleção
e no da bolha existem sempre
(n - 1) + (n - 2) + … + 1 = n(n - 1)/2 comparações.
No de inserção, se a seqüência está inicialmente
ordenada, existem n - 1 comparações, mas no pior caso pode
haver também n(n - 1)/2 comparações. O mesmo
ocorre com o método da bolha aperfeiçoado, como descrito em 3.3.
Quanto ao número de trocas no pior caso, o método de seleção,
com a melhoria descrita em 3.3, faz n - 1 trocas (uma por "varrida"),
enquanto os outros dois fazem n(n - 1)/2 trocas (uma a cada comparação,
se as tiras estiverem inicialmente em ordem inversa).
O instrutor conta que ele é muito azarado, e seu chefe sabe disso; este quer, portanto, saber qual a eficiência no pior caso. Como vimos, nesta situação os três métodos fazem o mesmo número de comparações, mas o de seleção leva vantagem por fazer menos trocas.
A partir disso introduz-se a noção de complexidade, que nos casos acima é da ordem de n2 (escreve-se O(n2)), como se observa pelo número calculado de comparações. Mostra-se que isso significa, para valores grandes de n, que se podem desprezar os outros termos com grau menor do que 2. Segue o resultado disso: dobrando-se o número de elementos, praticamente quadruplica-se o tempo levado.
- 5. Um método mais eficiente
Atenção: Escrevi um novo capítulo 5, com um método muito mais simples e ilustrativo. VWS.
5.1 Motivação
O instrutor relata que seu chefe provavelmente dirá: "Seus amigos levaram de 30 a 40 minutos para achar essas soluções. Será que se eles ficassem uma manhã inteira trabalhando obteriam algo melhor?" Pergunta aos participantes o que eles acham. Em geral, a maioria acha que é possível obter algo melhor, mas sempre há os que pensam não ser possível.
- É então apresentado um método mais eficiente, a ordenação por árvore ("tree sort"), que usa exatamente as mesmas regras R1 a R5, com as seguintes adições:
- R6. Permite-se o uso de mais compartimentos auxiliares.
R7. Pode-se apagar o conteúdo de uma tira e colocar outro em seu lugar.
- 5.2 Apresentação do método
- Esse método é apresentado no quadro-negro, da seguinte forma:
- i) Colocam-se 8 números um ao lado do outro (fig. 4)
- Mostra-se que nos métodos anteriores fazia-se uma varredura de comparações para se guardar apenas uma informação: qual o menor (maior) número da seqüência. Surge a idéia de se guardarem mais informações numa só varrida, ou melhor, a cada comparação guardar (mais precisamente, copiar) o resultado, por exemplo o menor número, em um compartimento auxiliar.
![]()
fig 4
- ii) Em uma primeira fase comparam-se os 8 números iniciais, dois a dois, resultando um nível de compartimentos auxiliares (fig. 5). Observe que para se saber qual o menor número da seqüência é suficiente procurá-lo entre os números deste nível.
- iii) Em uma fase seguinte, comparam-se os 4 números deste nível, dois a dois, obtendo-se um novo nível de compartimentos auxiliares.

fig. 5
iv) Repetem-se essas fazes até obter-se um nível com apenas um compartimento auxiliar (fig. 6).
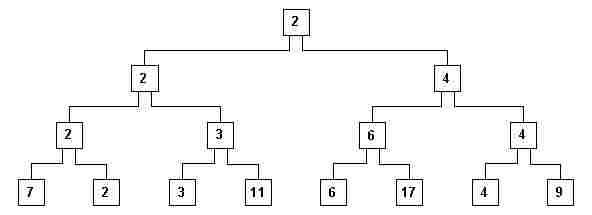
fig. 6
v) A estrutura que aparece na fig. 6 é chamada de árvore; cada compartimento é chamado de nó da árvore; o nó do nível superior é chamado de raiz e os nós do nível inferior são chamados de folhas (a árvore está de cabeça para baixo); os demais são chamados de nós intermediários. Um nó x é pai de um nó y (filho) se x está em um nível logo acima de y e está ligado a ele. Repare que na fig. 6 cada nó não-folha é pai de exatamente dois filhos (a árvore é binária). Generaliza-se esse conceito de nó pai e nó filho para nó ascendente e nó descendente.
vi) Observa-se que o menor elemento de todos fica na raiz (2, na fig. 6). Pois em cada nó não-folha vale a seguinte propriedade P: o seu conteúdo é menor ou igual a todos os seus descendentes. Ele é o primeiro elemento da seqüência ordenada.
vii) Elimina-se esse elemento da raiz e de todos os compartimentos onde ele aparece (caminho hierárquico da raiz até uma folha), apagando o dos compartimentos mostrados no quadro-negro (fig. 7).
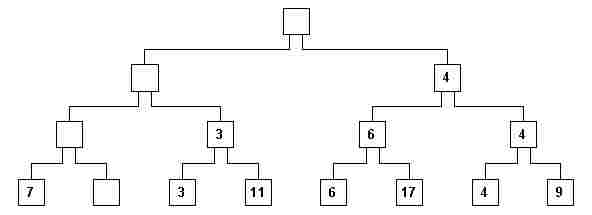
fig. 7
É interessante observar que as regras R1 a R5 do jogo continuam válidas: basta levantar as tiras do nó pai e de um dos nós filhos para concluir qual filho contém o mesmo valor que o pai.
viii) Percebe-se que a árvore deve ser refeita. Apenas os compartimentos apagados precisam ser reconstituídos pois deixaram de ter a propriedade P. Os conteúdos de compartimentos vazios não devem ser usados na comparação. Começando do nó folha vazio vê-se que seu irmão (com 7, na fig. 7) deve subir para o compartimento pai (fig. 8).
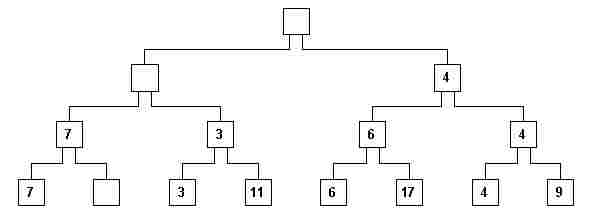
fig. 8
ix) Seria interessante conservar a técnica de fazer comparações, pis lidar com "vazio" é algo muito estranho. Para isso, pode-se perguntar aos participantes: que número colocariam no lugar da folha vazia, de tal modo que o 7 fosse sempre menor do que ele? Nossos participantes sempre responderam corretamente: infinito! Comenta-se que nos computadores não existe "infinito"; em geral colocar-se o maior número representável nas "tiras" da "memória". No quadro negro, colocamos o sinal de infinito em todos os nós que estavam vazios (fig. 9).
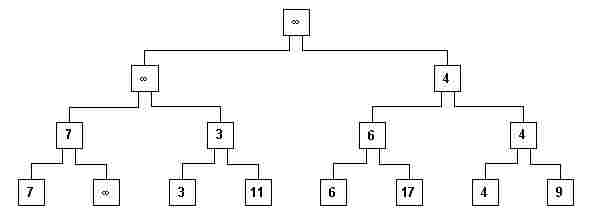
fig. 9
- x) Completa-se a reconstrução do caminho hierárquico até a raiz, que contém o próximo elemento da seqüência ordenada (fig. 10)
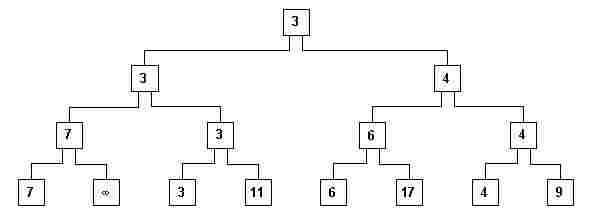
fig. 10
xi) Elimina-se a nova raiz, substituindo-se os elementos do seu caminho hierárquico por ¥ (fig. 11).
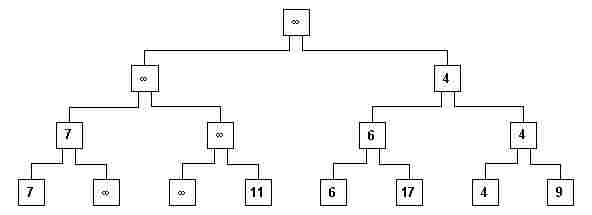
fig. 11
xii) Repete-se o processo até que os n números tenham sido extraídos da raiz.
5.3 Análise
Continuaremos a contar o número de comparações.
Para construir a árvore completa inicial (fig. 6), o número de comparações foi exatamente o número de compartimentos auxiliares criados. Se há n folhas, o nível dos seus pais terá n/2 compartimentos, o nível do pai destes n/4, e assim por diante, até 1.
Em geral os participantes notam que n não pode ser qualquer, achando que deve ser par. Observa-se então que se o n não é potência de 2, pode-se completar as folhas com ¥ até a próxima potência. O total de comparações é, portanto, para n potência de 2,
C = 1 + 2 + 4 + ... + n/4 + n/2
Temos a soma de uma PG com razão q = 2; a soma de uma PG é dada por
C = a1 (qk - 1) / (q - 1) (1)
Onde a1 é o primeiro termo e k o número de termos. Quantos termos existem? Tantos quanto o número de níveis com compartimentos auxiliares.
Observando a fig. 6 vemos que o nível 0 tem 1 elemento, o nível 1 tem 2, o nível 2 tem 22, o nível tem 23, …, e, portanto, o nível j (nível das folhas) tem 2j elementos. Mas sabemos que 2j = n. Logo, j = log2n (altura da árvore). Como queremos o número de níveis de 0 a j-1, temos k = j. Segue que k = log2n. Substituindo em (1):
C = 1 (2log n - 1) / (2 - 1) = n - 1
(Devido a restrições do editor de textos, escrevemos log em lugar de log2.)Portanto são empregadas n - 1 comparações para construir a árvore.
A substituição do nó raiz, e de todos os que têm o mesmo conteúdo, por ¥ toma log2n (altura da árvore) comparações na "descida"; aí é necessário pegar o irmão da folha onde foi colocado o último ¥ e fazer as comparações até chagar à raiz, refazendo o árvore. Teremos mais log2n comparações nessa subida. Portanto, para cada valor da raiz há 2log2n comparações. Como a primeira raiz fi deduzida à parte, e a última não precisa ser eliminada, temos (n - 1)2log2n comparações nessas "subidas" e "descidas". Logo o número de comparações é
n - 1 + 2(n - 1)log2n
O que dá uma complexidade de O(nlog2n), que é muito melhor que a dos 3 métodos iniciais que tinham O(n2), como se pode ver pela tabela dada a seguir, mostrando o número de comparações em cada caso. Os participantes ficam muito impressionados com a ordem de grandeza dos métodos O(n2) e com o fato de a ordenação por árvore, apesar de parecer mais complexa, ter tantas vantagens. Note-se que 2.048 elementos é um número muito pequeno perto do número de alunos de uma universidade ou de uma lista telefônica, por exemplo.
|
n |
n(n-1)/2 |
(n-1)+2(n-1)log2n |
Coluna 2 comparada com Coluna 3 |
|
1 |
0 |
0 |
= |
|
2 |
1 |
3 |
67% melhor |
|
4 |
6 |
15 |
60% melhor |
|
8 |
28 |
49 |
43% melhor |
|
16 |
120 |
135 |
12% melhor |
|
32 |
496 |
341 |
1.4 vezes pior |
|
64 |
2016 |
819 |
2.5 vezes pior |
|
128 |
8128 |
1905 |
4.3 vezes pior |
|
256 |
32640 |
4335 |
7.5 vezes pior |
|
512 |
130816 |
9709 |
13.5 vezes pior |
|
1024 |
523776 |
21483 |
24.4 vezes pior |
|
2048 |
2096128 |
47081 |
44.5 vezes pior |
É também interessante notar que nem sempre se deve usar a "ordenação por árvore", pois, conforme mostra a tabela, até n = 16 os outros métodos são mais eficientes.
Faz-se então um cálculo do número total de compartimentos necessários: n folhas mais n – 1 auxiliares, mais n para guardar os elementos da seqüência ordenada. Isso dá 3n – 1, ou seja, este método usa quase três vezes mais compartimentos do que os outros 3 iniciais. Menciona-se então que é possível empregar os próprios compartimentos iniciais como compartimentos auxiliares, obtendo-se o método denominado "heap sort" [1].
6. A noção de algoritmo ótimo
- O instrutor, referindo-se novamente ao seu chefe, lembrando que este é muito insistente, pergunta aos participantes o que será que o chefe reclamará em seguida.
Em geral, os participantes acertam a pergunta: existe algum método de ordenação ainda melhor?
O instrutor relata que é possível provar-se formalmente que não existe nenhum algoritmo de ordenação, baseado em comparações entre os elementos da seqüência, que tenha complexidade menor do que nlog2n . Dá uma indicação da maneira de demonstrar esse fato, empregando a árvore de comparações do "tree sort" (é preciso pelo menos comparar os elementos dois a dois, guardando-se o menor em cada nível). Chama a atenção para o fato de que não é portanto possível encontrar um algoritmo de ordenação (baseado em comparações) linear no tempo em função do número de elementos a serem ordenados. Por exemplo, se a ordenação de 1.000 números leva 1 segundo, a de 2.000 números inevitavelmente levará mais do que 2 segundos, o que provavelmente a maioria dos profissionais de processamento de dados desconhece (essa afirmação baseia-se em experiência do primeiro autor, colocando essa questão a profissionais de processamento de dados participantes de centenas de palestras e seminários que ele já deu).
Essa noção de algoritmo ótimo serve muito bem para ilustrar a importância da Teoria da Computação, em particular da Análise de Algoritmos. A maioria dos profissionais, senão a quase totalidade, fica satisfeita ao encontrar um algoritmo que resolve um problema, sem se questionar se existe algoritmo melhor e qual a sua "distância" do ótimo teórico.
Se o chefe do instrutor lhe encomendasse um algoritmo linear de ordenação por comparações, o conhecimento da teoria permitiria ao instrutor livrar-se da encomenda sem perder seu emprego por não tr conseguido cumprir a tarefa.
O problema da ordenação ótima está resolvido, mas existem vários outros problemas em aberto, que são objeto de pesquisa na área de análise de algoritmos. A pesquisa é feita tanto em obtenção de melhores algoritmos, como em demonstrações de complexidade ótimas, isto é, da não-existência de algoritmos melhores se o ótimo foi atingido.
Por exemplo, o problema do caixeiro viajante, isto é, qual o percurso que uma pessoa deve fazer par visitar n cidades com custo mínimo de viagem, ainda está em aberto quanto à possibilidade de se obter algum algoritmo de complexidade polinomial: todos os algoritmos conhecidos até hoje têm complexidade exponencial.
7. Questões computacionais
A partir dos exemplos das ordenações, pode-se agora introduzir conceitos fundamentais na ciência da Computação. Mais especificamente, o que faz uma pessoa dessa área ao defrontar-se com um problema? Ela procura algoritmos; precisamos então caracterizar o que é um algoritmo. Em seguida, ela procura descrever formalmente o algoritmo encontrado e programá-lo. Deve demonstrar que ele é correto, e analisá-lo quanto à complexidade verificando se ele é intratável quanto ao tempo de processamento.
7.1 O que é um algoritmo
Algoritmo é uma seqüência finita de passos elementares, cada um deles contendo uma operação matematicamente bem definida; a execução da seqüência sempre termina para quaisquer dados de entrada. Note-se que esta é uma caracterização e não uma definição formal (pode não ser possível provar que a execução termina).
7.2 Dificuldade de descrição formal, programação
O problema da ordenação mostrou os seguintes passos genéricos na resolução de um problema: 1) Resolução de um problema particular (ordenação de 8 números); 2) Generalização (ordenação de uma quantidade qualquer de números); 3) Descrição formal do método (necessária para posterior análise e programação para introdução em um computador).
A dificuldade de se descrever formalmente um método de solução de um problema ficou patente quando os grupos vencedores tentaram fazê-lo. Mostra-se que, a partir de uma descrição bem feita, a programação de um computador é trivial. Distribui-se uma listagem com os programa que implementam, em linguagem PASCAL, os métodos de ordenação descritos em 3.2 (V. Apêndice). Explica-se rapidamente cada comando.
7.3 "Corretude" de um algoritmo
A prova da corretude de um algoritmo consiste em mostrar que ele executa corretamente o proceso desejado, isto é, que chega à solução procurada. Existem métodos de prova formal da corretude, empregando Lógica Matemática. Nessa ‘rea há duas classes de problemas: a prova da execução correta e a prova de que a execução termina para quaisquer dados de entrada. Esta última questão é denominada de problema da parada.
Uma outra técnica é especificar matematicamente um problema, e transformas essa especificação usando regras formais de transformação (previamente demonstradas), até chegar-se a um algoritmo que pode ser formulado em uma linguagem de programação. Essa área é denominada Transformação Formal de Programas. Em lugar de provar que um programa está correto, faz-se sua dedução de maneira correta, o que pode ser muito mais simples e factível.
7.4 Problemas com soluções corretas ou incorretas
Seja p seguinte problema: Existem n cidades que devem ser interligadas por linhas de trem. É dado o custo de construção de cada trecho ligando pares de cidades (fig. 12), sendo que algumas ligações não são impossíveis (há lagos, serras, terrenos pantanosos, etc.) e portanto não são representadas. Procuram-se as interligações formando uma única rede conexa sem que nenhuma cidade fique fora dela, com o menor custo possível.
###fig. 12
Kruska (V. p. ex. [3]) propôs em 1956 em algoritmo, que é classificado dentro de uma denominação genérica de Método Guloso ("Greedy Algorithms"). Ele consiste inicialmente em ordenar os trechos segundo seus custos (aplicação dos algoritmos de ordenação…). Para o caso da fig. 12, obtém-se (note-se que, como exemplificamos custos diferentes 2 a 2, cada trecho fica identificado por seus custo):
1 3 5 6 7 9 12 15 16 20
Em seguida, percorre-se essa seqüência ordenada, incluindo na rede definitiva cada trecho que liga duas cidades entre as quais ainda não há um caminho. Os passos seriam:
a) 1; b) 1 3; c) 1 3 5; d) 1 3 5 6; e) 1 3 5 6 9; f) 1 3 5 6 9 15
Note-se que na transição do passo (d) par o passo (e) foi desprezado o trecho de custo 7, pois ligva duas cidades que já estavam interligadas indiretamente pelos trechos de custos 3 e 6. Note-se também que durante o processo podem-se ter várias sub-redes desconexas; por exemplo, após o passo (b) já temos essa situação, que permanece até o último passo, quando as duas sub-redes são então interligadas.
A rede resultante tem a forma de uma árvore denominada árvore de varredura mínima ("minimal spanning tree") [2, 3]. No exemplo, essa árvore tem raiz 1 e caminhos hierárquicos 1-5-9 e 1-15-3-6. Kruskal provou que ela tem realmente custo mínimo, o que resolve o problema.
É interessante discutir um pouco com os participantes a otimalidade da solução: por exemplo, será que ao se tomar o próximo trecho de menor custo não se poderá forçar a escolha futura de trechos mais caros e indesejáveis? Conta-se que a prova de otimalidade não é trivial, e é objeto de uma área de teoria da computação denominada de Teoria dos Grafos. É fundamental insistir na importância de se provar a corretude de um algoritmos; neste caso, que ele realmente encontra solucação ótima. É uma mostra de que o formalismo é essencial para comprovar alguma certeza ou alguma dúvida intuitiva.
O nome "método guloso" vem do fato de se escolher o melhor em cada passo. No entanto, não é um método que leva à solução ótima em qualquer problema. Por exemplo, suponhamos que um fazendeiro-zoólogo crie vários animais: leões, tigres, elefantes, zebras, girafas, etc. Para cada animal, ee tem um lucro associado à sua venda. Ele recebe uma encomenda de animais, independente da espécie. O problema é fazer um único transporte levando os animais que dêem o maior lucro total. Infelizmente, não é possível transportar quaisquer animais ao mesmo tempo: por exemplo, os leões são incompatíveis com as zebras (nem todas chegariam intactas ao destino…).
O método guloso não dá a solução ótima. Por exemplo, suponhamos que o lucro de um leão seja 20 e de cada zebra 2; só que há um único leão e 11 zebras. O método guloso escolheria inicialmente o leão, mas as zebras todas juntas dariam mais lucro.
O problema genérico é denominado conjunto independente máximo. Não se conhece um algoritmo de complexidade polinomial no tempo para a solução ótima desse problema. Os algoritmos existentes usam combinações dos elementos nos conjuntos, o que resulta em complexidade fatorial. No próximo item damos um exemplo dessa complexidade, mostrando como é desastrosa.
Um exemplo simples de problema com solução inerentemente ineficiente é o seguinte. Um indústria projetou uma máquina de calcular com mostrador e cálculos de 8 dígitos. Ela deseja testar caa calculadora produzida para verificar se seu funcionamento é perfeito. Um brilhante técnico resolve construir um aparelho para fazer testes exaustivos.
No caso de somas, o aparelho introduz as duas parcelas, e verifico o resultado obtido comparando-o com o esperado correto. Se o aparelho tiver capacidade para testar 1 milhão de somas por segundo (essa velocidade é muitíssimo maior do que a capacidade das calculadoras, pois se estas efetuarem um cálculo em 1/10 de segundo já terão velocidade mais do que suficiente para seus fins), quanto tempo levará para testar todas as somas possíveis? Temos 108 números diferentes possíveis em cada parcela, portanto 1016 combinações possíveis a serem testadas. Isso levará 1010 segundos de teste. Supondo 10.000 segundos por hora (em lugar de 3600), temos 106 horas; supondo 25 horas por dia, temos 4.104 dias; supondo 400 dias por ano temos um total (por baixo…) de 100 anos. Isto é, o problema é totalmente intratável por esse método. (Note-se que isso prova que as calculadoras não são exaustivamente testadas…. É um maravilha da engenharia eletrônica que, com poucos testes, possa-se concluir pela "corretude" da máquina.)
Em geral, problemas de simulação de jogos são dessa natureza: é necessário testar muitas combinações (as possíveis jogadas em cada situação), o que impossibilita seu tratamento por computador, a não ser que se apliquem estratégias de diminuição das combinações a serem testadas. Esse é um assunto tratado na área de algoritmos de "Inteligência Artificial". É interessante mencionar que esses algoritmos não têm nada a ver com nossa maneira de jogar. De fato, um Grande Mestre de xadrez não consegue saber e descrever o processo de intuição que o leva a deduzir o melhor lance para cada situação.
8. Resultados
Através das atividades aqui descritas, dá-se introdução a uma ampla gama de conceitos fundamentais da Teoria da Computação. Como se viu, essa introdução começa com a manipulações físicas pelos participantes, evitando-se assim um ensino demasiadamente abstrato e sem ligação com a realidade dos estudantes [4]. Nenhuma tela de computador pode substituir a atividade física dos estudantes, pois esta pode envolver objetos reais, e não abstratos como no caso da tela. Nossa proposta envolve ainda um aspecto social, pela formação dos grupos, que podem discutir não só no campo das idéias mas "fazendo com as mãos". Posteriormente chega-se ao nível puramente abstrato, mas este fica relacionado com a experiência física. Nesse sentido, temos aqui um exemplo de ensino "bottom-up", que nos parece muito mais adequado. O exemplo, que no caso é concreto, precede a abstração; ao chegar-se a ela o estudante não vai considerá-la como algo "estratosférico", fora de sua experiência.
Nossa experiência tem demonstrado que a atividade física estimula a criatividade. De fato, os participantes têm manifestado que jamais teriam chegado aos algoritmos de ordenação se não tivessem manuseado as cartolinas.
Durante as atividades aparecem conceitos matemáticos já vistos pelos alunos: somas de progressões, logaritmos e suas propriedades, combinações. Em duas das avaliações preenchidas pelos participantes logo após o evento encontram-se as seguintes frases (sic):
"A atividade é válida principalmente para quem não sabe por que se está aprendendo Matemática na escola. Pois com os exemplos concretos dados, é capaz de se entender o porquê de tanta teoria." "… Pude perceber melhor que realmente iremos usar a Matemática aprendida na escola."
O material didático e as regras do jogo (V. item 2) foram projetados para que as soluções encontradas pelos participantes pudesses ser "algoritmizadas"e se aproximasses de um programa de computador. Cremos ser essencial que se mude a imagem que os estudantes fazem da computação, deturpada pela associação com joguinhos eletrônicos e sua emoção. Nossos alunos de "Introdução à Computação" na USP ficam invariavelmente decepcionados com nossa computação conceitual: a sua expectativa era outra. Assim, o fato de as atividades aqui descritas não utilizarem um computador vem ao encontro dessa mudança de imagem. Um dos participantes escreveu (sic): "O curso [atividade] me mostrou que fazer um curso assim [nosso Bacharelado em Ciência da Computação] não é ficar mexendo em um computador o dia todo."
Foram realizadas 11 atividades, até o momento de escrever este trabalho, com um total de aproximadamente 450 participantes. A grande maioria destes escreveu, na avaliação, que nào tinha tido dificuldade em acompanhar os algoritmos apresentados e as respectivas análises.
Muito se fala sobre o uso de computadores em escolas. O primeiro autor já teve oportunidade de expressar sua opinião de que computadores devem ser usados somente no último ano do ensino médio, para ensino de computação prática (V. [4] e suas extensões [6, 7], bem como artigos em seu "site"). A atividade "Dia da Computação" que organizou [5, 8, 9] tem mostrado que estudantes de menos de 17 anos não têm em geral interesse pelos conceituais e estruturais da computação. Assim, ele recomenda também na atividade aqui descrita que essa idade seja aproximadamente seguida, isto é, que ela seja aplicada a alunos da 3a série do Colegial ou de nível superior. Tivemos a oportunidade de mostrar aqui como conceitos novos, importantes e abrangentes podem ser introduzidos de modo a esclarecer os estudantes sobre aspectos fundamentais da computação.
Cremos que um lugar adequado para estas atividades que, insistimos, não necessitam de computadores, é a disciplina de Matemática. A computação, do ponto de vista algorítmico, está mais para a Matemática do que para qualquer outra ciência.
Referências
[1] Wirth, N. Algoritmos e Estrururas de Dados (Trad. C.M.Lee). Rio de Janeiro: Prentice Hall, 1989.
[2] Harel, D. Algorithmics – the Spirit of Computing. Reading: Addison-Wesley, 1987.
[3] Terada, R. Desenvolvimento de Algoritmos e Estruturas de Dados. São Paulo: McGraw Hill, 1991.
[4] Chaves, E.O.C. e Setzer, V.W. O uso de computadores em escolas: fundamentos e críticas. São Paulo: Scipione 1987.
[5] Setzer, V.W e R.Hirata Jr. O Dia da Computação: uma introdução rápida ao computador e à computação. Ciência e Cultura 42, 5/6 (maio/junho 1990), pp. 333-340 e Caderno da Revista do Professor de Matemática, Vol. 4, No. 1, 1993, pgs. 27-38) .
[6] Setzer, V.W. Computers in Education. Edinburgh: Floris Books, 1989. Ver também a versão estendida em alemão, Computer in der Schule? Thesen und Argumente. Stuttgart: Verlag Freies Geistesleben, 1992.
[7] Setzer, V.W. Computadores na educação: por que, quando e como. A sair como artigo do Vol. 8 da coleção "Ensaios Transversais", São Paulo: Ed. Escrituras, 2001. Versão original disponível no "site" do primeiro autor.
[8] Setzer, V.W.The Paper Computer – a pedagogical activity for the introduction of basic concepts of computers. Disponível no "site" do primeiro autor.
[9] Setzer, V.W. The HIPO computer – a tool for teaching bsic computer principles through machine language. Disponível no "site" do primeiro autor, inclusive com o simulador do computador HIPO em português e em inglês, para "download".
APÊNDICE
Programas em PASCAL
Program Seleção;
{ Dados N e uma seqüência de N números, coloca-os
em}
{ ordem crescente pelo método de seleção. No
final, }
{ imprime a seqüência ordenada.}
Var
N, { N/umero de elementos da seqüência }
I, J: integer; { Índices }
C: array[1..100] of real; { A seqüência
tem no máximo 100 elementos}
Aux: real; { Variável auxiliar usada na troca de conteúdo
entre 2 compartimentos}
Begin
{ Entrada da seqüência }
write(’Entre tamanho da seqüência, <= 100’);
readln(N);
for I:=1 to N
do begin
write(’Entre
o próximo número da seqüência’);
readln(C[I]);
end;
{ Ordenação }
for I:=1 to N-1
do for J:=I+1 to N
do if
C[I] > C[J]
then
begin { Troca C[I] com C[J] }
Aux:=C[I];
C[I]:=C[J]; C[J]:=Aux
end;
{ Impressão }
writeln(’The ordered sequence is:’);
for I:=1 to N
do write(C[I],’ ’);
end.
Program Bolha;
{ Dados N e uma seqüência de N números, coloca-os
em }
{ ordem crescente pelo método da bolha. No final, }
{ imprime a seqüência ordenada. }
Var
...
Begin
...
{ Ordenação }
for I:=N downto 2
do for J:=1 to I-1
do if
C[J] > C[J+1]
then
begin { Troca C[J] com C[J+1] }
Aux:=C[J];
C[J]:=C[J+1]; C[J+1]:=Aux
end;
...
end.
Program Inserção;
{ Dados N e uma seqüência de N números, coloca-os
em }
{ ordem crescente pelo método da inserção.
No final, }
{ imprime a seqüência ordenada. }
Var
...
Begin
...
{ Ordenação }
for I:=2 to N
do begin
J:=I;
while
(C[J] < C[J-1]) and (J > 1)
do
begin { troca C[J] com C[J-1] }
Aux:=C[J];
C[J]:=C[J-1]; C[J-1]:=Aux
end;
end;
...
end.