Coberturas por vértices
Imagine um conjunto de salas
interligadas por corredores.
Um guarda postado numa sala
é capaz de vigiar todos os corredores que convergem sobre a sala.
Queremos determinar o
menor número de guardas capaz de
vigiar todos os corredores.
Esta é uma instância do
problema da cobertura mínima por vértices.
Esta página foi inspirada, em parte,
no capítulo 10 do livro de Kleinberg e Tardos.
Cobertura por vértices
Dizemos que um conjunto C de vértices de um
grafo
cobre uma aresta vw do grafo
se v pertence a C
ou w pertence a C
(ou ambos).
Uma cobertura por vértices
(= vertex cover)
de um grafo,
ou simplesmente cobertura,
é um conjunto de vértices
que cobre todas as arestas.
Em outras palavras, uma cobertura é um conjunto de vértices
que contém pelo menos uma das pontas de cada aresta.
Exercícios 1
-
★
Escreva um algoritmo que receba um grafo G
e um subconjunto S de V(G)
e decida se S é uma cobertura.
Quanto tempo seu algoritmo consome?
(Suponha que G é dado por uma
matriz de adjacência.)
-
Escreva um algoritmo para decidir se um grafo tem uma
cobertura com 2 ou menos vértices.
Cobertura mínima
Uma cobertura de um grafo G é mínima
se não existe outra menor.
Em outras palavras, uma cobertura X
de G é mínima se
não existe cobertura S de G
tal que ⎮S⎮ < ⎮X⎮.
Problema do Cobertura Mínima:
Encontrar uma cobertura mínima de um grafo.
O problema é notoriamente difícil.
É claro que um algoritmo de força bruta
,
que examina todos os 2n subconjuntos
do conjunto de vértices do grafo,
resolve o problema.
Mas não se descobriu (ainda?)
um algoritmo que seja substancialmente mais rápido.
Mais precisamente, não se conhece um algoritmo
polinomial
para o problema.
É possível até que um tal algoritmo não exista.
(Veja a página Complexidade e problemas NP-completos.)
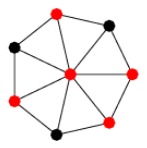
Exemplo A.
A figura mostra uma cobertura mínima de um grafo
(veja os vértices vermelhos).
Exercícios 2
-
★
Dê um exemplo de um grafo com n vértices
que tenha uma cobertura com 1 vértice.
Dê outro exemplo em que uma cobertura mínima
tenha n − 1 vértices.
É verdade que toda cobertura mínima
tem menos que n vértices?
-
Qual o tamanho de uma cobertura mínima
de um grafo que consiste em um
circuito simples
e nada mais?
-
Qual o tamanho de uma cobertura mínima
de um grafo que consiste em um
caminho simples e nada mais.
-
★
Encontre coberturas mínimas dos grafos da figura.
-
★
Seja X uma cobertura mínima de um grafo.
É verdade toda aresta do grafo tem apenas uma
de suas pontas em X?
-
Grafo do cavalo.
Encontre uma cobertura mínima no
grafo do cavalo 3-por-3.
Repita o exercício para o grafo do cavalo 4-por-4 e para o grafo do cavalo 5-por-5.
-
Grafo da dama.
Encontre uma cobertura mínima no
grafo da dama 5-por-5.
Repita o exercício para o grafo da dama 8-por-8.
-
Seja m o número de arestas de um grafo com n vértices.
Mostre que toda cobertura do grafo tem pelo menos m/(n − 1)
vértices.
-
Desafio!
Invente um algoritmo que resolva o problema da cobertura mínima
em Ο(n9) unidades de tempo.
(Você pode trocar
9
por seu expoente favorito.)
Redução ao problema do conjunto independente máximo
Para qualquer conjunto C de vértices de um grafo G,
denotamos por G − C
o subgrafo induzido pelo complemento V − C
de C.
Teorema:
Um subconjunto C
de V
é uma cobertura se e somente se
E(G − C)
é vazio.
Em outras palavras,
C é uma cobertura se e somente se V − C
é independente.
Prova:
Suponha que C é uma cobertura.
Então toda aresta de G tem pelo menos
uma ponta em C.
Em outras palavras, nenhuma aresta de G
tem ambas as pontas fora de C.
Logo, V − C
é independente.
Isso prova a parte somente se
do teorema.
Agora suponha que I é um conjunto independente.
Então nenhuma aresta G tem ambas as pontas em I.
Em outras palavras,
toda aresta tem pelo menos uma ponta em V − I.
Isso prova a parte se
do teorema.
O teorema tem a seguinte consequência:
um conjunto X de vértices é uma cobertura mínima
se e somente se V − X
é um conjunto independente máximo.
Portanto,
qualquer algoritmo para o problema do conjunto independente máximo
pode ser usado para resolver o problema da cobertura mínima
(e vice-versa).
Exercícios 3
-
Seja C uma cobertura mínima de um grafo G.
Prove que V − C
é um conjunto independente máximo.
-
Seja C uma cobertura máxima e
I um conjunto independente mínimo de um grafo G.
É verdade que C = V − I?
-
Seja C uma cobertura mínima e
I um conjunto independente máximo de um grafo G.
É verdade que C = V − I?
-
Seja G um grafo com n vértices,
c o tamanho de uma cobertura mínima de G,
e i o tamanho de um conjunto independente máximo
de G.
Mostre que c = n − i.
-
Mostre como um algoritmo para o problema do conjunto independente máximo
pode ser usado para resolver o problema da cobertura mínima.
-
★
Prove que o vizinho de toda folha de uma floresta
pertence a alguma cobertura mínima.
-
★
Cobertura mínima de floresta.
Descreva um algoritmo eficiente que resolva o
problema da cobertura mínima restrito a
florestas.
(Sugestão:
veja o algoritmo para conjuntos independentes máximos em florestas.)
-
Grafos bipartidos.
Um grafo é bipartido
(ou bicromático)
se tem uma cobertura que é um conjunto independente.
Escreva um algoritmo que decida se um dado grafo é bipartido.
O algoritmo deve consumir
Ο(n + m)
unidades de tempo,
ao processar um grafo com n vértices e m arestas.
Minimal versus mínimo
Uma cobertura C de um grafo G
é minimal
se não for superconjunto próprio de outra cobertura,
ou seja,
se não existe uma cobertura D
tal que D ⊂ C.
É claro que toda cobertura mínima é minimal,
mas a recíproca está muito longe de ser verdadeira.
(Veja um dos exercícios abaixo.)
Exemplo B.
A figura mostra uma cobertura minimal
(vértices vermelhos)
de um grafo.
Essa cobertura não é mínima.
O seguinte algoritmo recebe um grafo G
e devolve uma cobertura minimal.
O código usa a notação N(v)
para designar o conjunto de todos os vizinhos do vértice v.
|
Cobertura-Minimal (G)
|
|
1
.
S := V(G)
|
|
2
.
para cada v em V(G)
|
|
3
.ooo
se N(v) ⊆ S
|
|
4
.oooooo
então S := S − { v }
|
|
5
.
devolva S
|
O algoritmo está correto?
Na linha 5, o conjunto S é uma cobertura?
é uma cobertura minimal?
Exercícios 4
-
★
Mostre que uma cobertura minimal
pode ser arbitrariamente maior que uma cobertura mínima.
-
Seja G um grafo e S
um subconjunto de V(G).
Prove que S é uma cobertura minimal
se e somente se V − S
é um conjunto independente maximal.
-
★
Caracterização da minimalidade.
Seja C uma cobertura de um grafo.
Mostre que C é minimal
se e somente se
todo vértice em C
tem algum vizinho fora de C.
[Solução]
-
★
Prove que o algoritmo
Cobertura-Minimal está correto.
Qual o consumo de tempo do algoritmo
(em termos do número n de vértices
e do número m de arestas de G)?
-
Escreva o algoritmo Cobertura-Minimal
em um nível de abastração mais baixo
(isto é, mais próximo de uma linguagem de programação como C,
por exemplo).
Suponha que o grafo e representado por sua
matriz de adjacência
e calcule o vetor característico
de uma cobertura minimal.