Algoritmos para Grafos | Índice
Nossa implementação do algoritmo de Ford-Fulkerson tem uma camada interna (que procura por pseudocaminhos aumentadores) e uma camada externa (que usa os pseudocaminhos para calcular um fluxo máximo). Este capítulo trata da camada externa. Implementações da camada interna serão discutidas nos capítulos seguintes.
A escolha de uma boa estrutura de dados é fundamental para uma implementação eficiente do algoritmo de Ford-Fulkerson. Teremos que fazer várias decisões de projeto, nem todas muito confortáveis.
Sumário:
Em princípio, a estrutura de dados de que precisamos
para representar grafos capacitados
é muito simples:
basta adaptar a estrutura que já definimos
para grafos com custos nos arcos,
trocando custo
por capacidade
.
Entretanto,
uma implementação eficiente do algoritmo de Ford-Fulkerson
exige de uma estrutura de dados mais rica,
que permita a manipulação de pseudocaminhos.
Para dar suporte a essa estrutura mais rica,
convém expandir os nós das listas de adjacência,
adicionando a eles alguns campos auxiliares.
Assim, além dos campos usuais w e next,
teremos
Um nó com esses campos será chamado nó expandido.
typedef struct node *link; struct node { // nó expandido vertex w; int c; int flow; int type; link twin; link next; };
Para especificar uma instância do
problema do fluxo máximo,
somente os campos w, c,
e next são necessários.
Suporemos portanto que
os campos flow,
type, e twin
estão em branco
por enquanto;
eles serão preenchidos durante a execução do algoritmo.
6 8 0 5 0-1 2 0-2 3 1-3 3 1-4 1 2-3 1 2-4 1 3-5 2 4-5 3
É difícil procurar pseudocaminhos
num grafo
por causa dos arcos reversos dos pseudocaminhos.
Para enfrentar essa dificuldade,
vamos acrescentar alguns arcos auxiliares ao nosso grafo.
Graças a esses arcos,
será possível trabalhar só com
caminhos tradicionais,
sem o pseudo
.
Para cada arco v-w, acrescentaremos ao grafo um novo arco w-v, antiparalelo a v-w. Diremos que os novos arcos são artificiais e os antigos são originais. Da mesma forma que o arco original v-w é representado por um nó expandido a na lista adj[v], o correspondente arco artificial w-v será representado por um nó expandido b na lista adj[w]:
b = malloc( sizeof (struct node));
b->w = v;
b->twin = a;
a->twin = b;
b->next = G->adj[w];
G->adj[w] = b;
Usaremos o campo twin para que a possa ser facilmente localizado a partir de b e vice-versa. O campo type indicará o tipo do arco: +1 se o arco for original e -1 se for artificial:
a->type = +1;
b->type = -1;
O novo grafo, depois da adição dos arcos artificiais, será chamado grafo expandido. (Os arcos artificiais introduzem um pequeno desconforto técnico: se o grafo original tiver arcos antiparalelos, o correspondente grafo expandido terá arcos paralelos, o que entra em choque com nossa proibição de tais arcos. Felizmente, nossa estrutura de dados aceita arcos paralelos com naturalidade.)
Ao trabalhar com o grafo expandido, gostaríamos de ignorar a distinção entre arcos artificiais e originais, tratando todos da mesma maneira. Para isso, é preciso que cada arco artificial tenha uma capacidade bem como um fluxo. Como essa capacidade e esse fluxo devem ser definidos? Essa é uma decisão de projeto importante. Adotaremos a seguinte definição: cada arco artificial terá capacidade zero e fluxo igual ao negativo do fluxo no correspondente arco original:
b->c = 0;
b->flow = -a->flow;
Como flow é positivo nos arcos originais, a desigualdade flow ≤ c valerá em todo arco artificial. Essa desigualdade também vale, por hipótese, em todos os arcos originais. (Mas os campos flow dos nós não definem um fluxo no grafo expandido.)
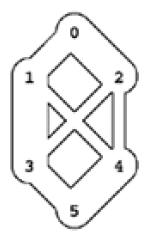
Exemplo A. Considere o grafo cujos arcos estão indicados a seguir junto com as respectivas capacidades (segunda linha da tabela). O vértice inicial é 0 e o vértice final é 5. A terceira linha da tabela define um fluxo que respeita as capacidades.
0-1 0-2 1-3 1-4 2-3 2-4 3-5 4-5 2 3 3 1 1 1 2 3 2 2 1 1 1 1 2 2
Veja a seguir o correspondente grafo expandido (os arcos artificiais estão em vermelho):
0-1 0-2 1-3 1-4 2-3 2-4 3-5 4-5 1-0 2-0 3-1 4-1 3-2 4-2 5-3 5-4 2 3 3 1 1 1 2 3 0 0 0 0 0 0 0 0 2 2 1 1 1 1 2 2 -2 -2 -1 -1 -1 -1 -2 -2
macarronadaque represente um dado fluxo num grafo. Sua função deve receber um grafo expandido, com vértice inicial s, vértice final t, e um fluxo (representado nos campos flow dos nós). Sua função deve imprimir uma coleção de caminhos que represente o fluxo. Para cada caminho, deve imprimir também a quantidade de fluxo que cada caminho conduz.
Com a introdução dos arcos artificiais, os pseudocaminhos do grafo original podem ser representados por caminhos tradicionais no grafo expandido: os arcos artificiais de um caminho no grafo expandido representam os arcos reversos do correspondente pseudocaminho no grafo original. Assim, por exemplo, em vez de um pseudocaminho aumentador 0-2-3=1-4-5 no grafo original, teremos o caminho aumentador 0-2-3=1-4-5 no grafo expandido.)
Suponha que o grafo original tem um certo fluxo (representado pelos campos flow dos seus arcos originais e artificiais). Então a capacidade residual de um arco, seja ele original ou artificial, é a diferença
c − flow .
Como o fluxo é positivo nos arcos originais, a capacidade residual dos arcos artificiais é positiva. Se o fluxo respeita as capacidades dos arcos originais (ou seja, se flow ≤ c), a capacidade residual dos arcos originais também é positiva.
A capacidade residual de um caminho é a menor das capacidades residuais de seus arcos. Um caminho de s a t no grafo expandido é aumentador se tiver capacidade residual estritamente positiva. Essa definição corresponde, exatamente, ao conceito de pseudocaminho aumentador no grafo capacitado original.
Exemplo B. Considere o grafo capacitado abaixo, com vértice inicial 0 e vértice final 5. A segunda linha da tabela especifica as capacidades e a terceira dá um fluxo.
0-1 0-2 1-3 1-4 2-3 2-4 3-5 4-5 2 3 3 1 1 1 2 3 2 1 2 0 0 1 2 1
A tabela seguinte mostra os arcos do grafo expandido e suas capacidades residuais. Os arcos artificiais estão pintados de vermelho.
0-1 0-2 1-3 1-4 2-3 2-4 3-5 4-5 1-0 2-0 3-1 4-1 3-2 4-2 5-3 5-4 0 2 1 1 1 0 0 2 2 1 2 0 0 1 2 1
O caminho 0-2-3=1-4-5, por exemplo, tem capacidade residual 1.
A função GRAPHmaxFlow() abaixo implementa o
algoritmo de Ford-Fulkerson.
Ela calcula um fluxo máximo
num grafo capacitado G
com vértice inicial s e vértice final t.
O grafo G não tem arcos artificiais,
mas os nós de suas listas de adjacência são expandidos
(estando os campos flow, type e twin
em branco
).
A função GRAPHmaxFlow() tem três fases:
/* Esta função devolve a intensidade de um fluxo máximo no grafo capacitado G com vértice inicial s e vértice final t. O fluxo é armazenado nos campos flow dos nós das listas de adjacência. O código supõe que G tem no máximo 1000 vértices. (Código inspirado na segunda parte do programa 22.3 de Sedgewick.) */
int GRAPHmaxFlow( Graph G, vertex s, vertex t) { vertex pa[1000]; // parent vertex link parc[1000]; // parent arc expandGraph( G); for (vertex v = 0; v < G->V; ++v) for (link a = G->adj[v]; a != NULL; a = a->next) a->flow = 0; int intensity = 0; while (true) { int delta = AugmPath( G, s, t, pa, parc); // delta = cap residual de caminho aumentador if (delta == 0) break; for (vertex w = t; w != s; w = pa[w]) { link a = parc[w]; a->flow += delta; a->twin->flow -= delta; } intensity += delta; } contractGraph( G); return intensity; }
/* Acrescenta os arcos artificiais ao grafo G e preenche os campos type e twin de todos os nós das listas adj[]. (Os novos nós ficam concentrados no início das listas adj[]. */
void expandGraph( Graph G) { for (vertex v = 0; v < G->V; ++v) for (link a = G->adj[v]; a != NULL; a = a->next) a->type = +1; for (vertex v = 0; v < G->V; ++v) for (link a = G->adj[v]; a != NULL; a = a->next) if (a->type == +1) { link b = malloc( sizeof (struct node)); b->w = v; b->c = 0; b->type = -1; b->twin = a; a->twin = b; b->next = G->adj[a->w]; G->adj[a->w] = b; } }
/* A função contractGraph() desfaz o efeito de expandGraph(), removendo todos os arcos artificiais do grafo. (A função supõe que os nós que representam os arcos artificiais estão concentrados no início das listas adj[].) */
void contractGraph( Graph G) { for (vertex v = 0; v < G->V; ++v) { link a = G->adj[v]; while (a != NULL && a->type == -1) { link b = a; G->adj[v] = a = a->next; free( b); } } }
[Juan Gutiérrez Alva apontou um erro na minha versão anterior da função GRAPHmaxFlow().] Parte substancial do código de GRAPHmaxFlow() está escondida na função AugmPath(), que tem a missão de encontrar um caminho aumentador (= augmenting path) no grafo expandido e devolver a capacidade residual desse caminho. Se não existe caminho aumentador, a função devolve 0. Senão, o caminho é armazenado nos vetores pa[] e parc[] (os nomes dos vetores são abreviaturas de parent e parent arc respectivamente) da seguinte maneira: para cada vértice w do caminho,
Observe como o bloco de linhas
for (vertex w = t; w != s; w = pa[w]) {
link a = parc[w];
a->flow += delta;
a->twin->flow -= delta;
}
de GRAPHmaxFlow() trata corretamente de enviar delta unidade de fluxo ao longo do arco representado por a, quer o arco seja original quer artificial.
Quanto à função AugmPath(), duas diferentes implementações são discutidas a seguir nos capítulos Caminhos aumentadores mínimos e Caminhos aumentadores de capacidade máxima.
Exemplo C. Considere novamente o grafo capacitado do exemplo A com vértice inicial 0, vértice final 5, e as capacidades indicadas a seguir.
0-1 0-2 1-3 1-4 2-3 2-4 3-5 4-5 2 3 3 1 1 1 2 3
Depois de construir o grafo expandido, a função GRAPHmaxFlow() executa quatro iterações. As sucessivas invocações de AugmPath() produzem a seguinte sequência de caminhos aumentadores (os arcos artificiais estão indicados em vermelho).
0-1-3-5
0-2-4-5
0-2-3=1-4-5
(A capacidade residual, delta, do primeiro caminho aumentador é 2. Cada um dos demais tem capacidade residual 1.) Essa sequência de aumentos produz o fluxo máximo indicado a seguir.
0-1 0-2 1-3 1-4 2-3 2-4 3-5 4-5 2 2 1 1 1 1 2 2
A intensidade do fluxo é 4.