Introdução elementar à Lógica
Os comandos para desvio de fluxo de execução dependem da uso de condições lógica (ou expressões lógicas), sendo essencial para a construção de algoritmos, pois esse tipo de comando permite algoritmos cujo "comportamento" é alterado de acordo com os dados de entrada. Assim, nesta seção apresento os fundamentos para a construção de expressões lógicas: os princípio da lógica booleana, lembrando o que é tabela verdade e as leis de De Morgan.
1. Sentenças lógicas e conjuntos
A lógica é essencial para a matemática como ciência, ela ajuda a estruturar a linguagem matemática. Pode-se considerar cada afirmação matemática como uma sentença lógica, um teorema pode ser visto como uma sentença do tipo A implica B.
Existem três operadores básicos para lógica, a negação, a conjunção e a disjunção, respectivamente os operadores não, e e ou. Seu significado pode ser entendido pelas tabelas verdade, vide tabela 1.
Nota sobre a linguagem C: os operadores lógicos em C são respectivamente !, && e ||.
Exemplo C: Comparação com operadores relacionais ">" e "<" e com operadores lógicos "!" e "&&".
Nota sobre a linguagem Python: os operadores lógicos em Python são respectivamente not, and e or.
Exemplo Python: Comparação com operadores relacionais ">" e "<" e com operadores lógicos "not" e "and".
De outra parte, cada sentença lógica pode ser examinada sob o de vista de conjuntos. No exemplo A implica B, se entendermos A e B como conjuntos, a implicação indica que o conjunto A está contido no conjunto B, pois se a propriedade A está satisfeita, então propriedade B está satisfeita. Isso está ilustrado na figura 1.a, na qual usamos diagrama de Venn.
Assim a sentença não A pode ser entendida como o complemento do conjunto A, ilustrado na figura 1.b. E podemos compor as sentenças, por exemplo, criando a sentença "não A e B", ou seja, como conjunto, os elementos que não estão em A e que simultaneamente estão em B, como ilustrado na figura 1.c.
A figura 1.a apresenta o conjunto B (azul mais claro), contendo o conjunto A. A figura 1.b apresenta o complemento ao conjunto A (azul mais claro), ou seja, os elementos que não estão em A. A figura 1.c mostra a interseção (equivalente à conjunção - e lógico) entre o "complemento ao conjunto A" e o conjunto B (azul mais claro), ou seja, a interseção com dos elementos que estão no complemento de A com aqueles que estão em B.
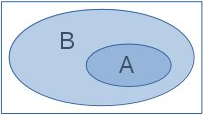
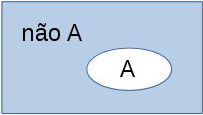
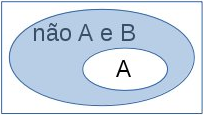
Fig. 1. Representação gráfica com conjuntos: (a) A contido em B; (b) complemento de A; e (c) B\A (em B, mas não em A).
2. Tabela verdade
Do ponto de vista da lógica, cada sentença deve ser ou verdadeira ou falsa (isto é, pode ocorrer apenas uma das duas opções, sendo um "ou exclusivo"). Em termos práticos para a programação, o que interessa é a construção de expressões lógicas (EL), de modo análogo às expressões aritméticas (EA). Assim, a EL mais elementar é aquela com a constante verdadeiro ou falso, como uma EA elementar seria um número.
Os operadores lógicos são a negação inverte o valor lógico da expressão, a conjunção (e) resulta verdadeiro se, e somente se, ambos os operandos são verdadeiro e a disjunção (ou) resulta falso se, e somente se, ambos os itens forem falsos. O resultado de cada um desses operadores é dado por sua tabela verdade, como indicada abaixo.
As tabelas abaixo representam as sentenças das operações básicas não A, A e B e A ou B. Simplificaremos escrevendo "verd" para "verdadeiro" (1 em C e true em Python) e "fals" para "falso" (0 em C e false em Python).
|
|
|
De modo geral, para cada sentença, ou expressão lógica, pode-se construir sua corresponde tabela-verdade.
Assim, dada uma sentença formada com k itens lógicos (ou sentenças elementares),
pode-se fazer uma tabela com k+1 colunas, sendo a primeira formada pelo item 1,
a segunda pelo item 2 e assim por diante.
Por exemplo, se a sentença tem apenas um item (como na tabela 1.(a), k=1), existem 21 linhas e
na última coluna está precisamente o valor da expressão.
Se a sentença tiver dois itens (como na tabela 1.(b), k=2), então teremos 22=4 linhas e o valor lógico
resultante na última coluna.
Generalizando, uma expressão lógica com k itens terá (além da linha título) 2k linhas,
cada linha terá uma das possíveis combinações para os valores verdadeiro ou falso e em sua última
coluna k+1 o resultado da sentença completa.
Portanto, a tabela terá 2k linhas, cada linha terá uma combinação
possível para os valores verdadeiro ou falso.
Assim, dada uma sentença formada com k itens lógicos (ou sentenças elementares), pode-se fazer uma tabela com k+1 colunas, sendo a primeira formada pelo item 1, a segunda pelo item 2 e assim por diante. A coluna k+1 representa a sentença completa. Nesse caso a tabela terá 2k linhas, cada linha terá uma combinação possível para os valores verdadeiro ou falso.
Note que tanto a disjunção quanto a conjunção são operações
3. Leis de De Morgan
Do mesmo modo que na aritmética podemos compor expressões com diferentes operadores (como '+' e '-'), também podemos compor sentenças misturando os três operadores. Para isso é interessante perceber que valem as seguintes equivalências, denominadas leis de De Morgan:
"não (A ou B)" ≡ "(não A) e (não B)"
Se não estiver clara a equivalência, monte as tabelas verdade para cada par de sentença e observe que ambas produzem os mesmo resultados.
Algumas fontes para aprofundamento: na WikiPedia examinar os vocábulos De_Morgan%27s_laws ou Teoremas_de_De_Morgan. Se desejar aprofundar o entendimento sobre a linguagem matemática pegue a apostila do professor Ricardo Bianconi.
Leônidas de Oliveira Brandão
http://line.ime.usp.br
 :
:2021/07/14: várias quenas correções
2021/06/16: rodapé e numeração de seções
2021/05/09: vários acertos (conjunção, c maior...)
2020/08/19: várias pequenas correções, texto da seção "Tabela verdade" completamente reescrito
2020/08/15: novo formato, pequenas revisões
2020/08/07: revisão geral
2018/04/16: primeira versão