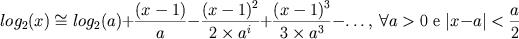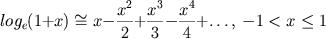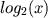 a partir de operações básicas (soma)
a partir de operações básicas (soma)
Problema
O computador só "sabe" fazer operações baseadas em somas, deste para computar a função
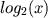 (ou outras como
(ou outras como 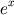 ,
,
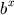 ,...) é necessário aplicar alguma técnica matemática que permita
reescrever a função na forma de um "polinômio equivalente".
,...) é necessário aplicar alguma técnica matemática que permita
reescrever a função na forma de um "polinômio equivalente".
Solução matemática
Uma solução seria aproximar a função por uma "parte" de uma série de Taylor. Entretanto isso gera um novo problema matemática:
Deste modo, fica claro a necessidade de algum "truque" matemática para conseguirmos calcular diferentes "log's". Uma vez que, a menos de uma divisão por constante, as funções logarítmicas são equivalentes, vamos escolher a segunda forma para trabalhar. A razão da equivalência é a conhecida identidade
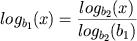 .
.
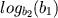 é uma constante, qualquer que seja o parâmetro
é uma constante, qualquer que seja o parâmetro  .
.
Como computar
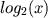 , para
, para 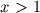 ?
?
Lema. Qualquer que seja
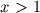 ,
,
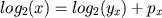 ,
,
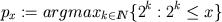 e
e
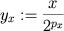 . Além disso,
. Além disso, 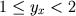 .
.
Deste modo podemos computar
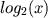 utilizando a identidade
utilizando a identidade 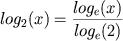 .
.
Teorema. Qualquer que seja
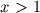 ,
,
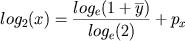 ,
,
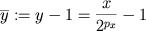 .
.
Portanto
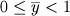 , e deste modo podemos utilizar a aproximação 2 para logaritmo neperiano.
Ou seja, com este último teorema é possível obter uma boa aproximação
para
, e deste modo podemos utilizar a aproximação 2 para logaritmo neperiano.
Ou seja, com este último teorema é possível obter uma boa aproximação
para 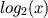 , qualquer que seja
, qualquer que seja  .
.
Implementação
- Construir uma função que determina
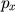 para um dado
para um dado 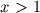 , de acordo com o lema anterior
(ou seja, dado
, de acordo com o lema anterior
(ou seja, dado  encontrar um natural
encontrar um natural 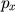 tal que
tal que 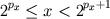 ).
).
- Construir uma função que computa
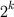 , para qualquer natural
, para qualquer natural 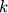 .
.
A utilidade desta função é testar a função anterior (ela não necessariamente precisa ser usada no cálculo final). - Construir uma função que computa uma aproximação de Taylor, com N termos,
para
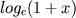 ,
, 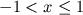 .
.
(esta função deverá ter 2 parâmetros, o N e o x) - O seu programa deve fazer duas coisas:
- Listar uma tabela na forma abaixo para verificar se sua função
"log" coincide com a função "log" da biblioteca C.
+--------+--------+---------+ | x |log_2(x)| log(x) | +--------+--------+---------+ | 2 | 1.000 | 1.000 | | 15 | 3.841 | 3.907 | | 43 | 5.420 | 5.426 | | 99 | 6.608 | 6.629 | | 211 | 7.688 | 7.721 | | 857 | 9.707 | 9.743 | | 3441 | 11.712 | 11.749 | | 13777 | 13.713 | 13.750 | | 110229 | 16.713 | 16.750 | | 881845 | 19.713 | 19.750 | +--------+--------+---------+
Para gerar esta tabela use o seguinte laço:#include <math.h> // esta linha vai no topo // do arquivo // para compilar este arq., com a biblioteca matemática // "math.h", no Linux, digite: gcc -lm -o nome.o nome.c #define LN2 log(2) // é interessante p/ só calcular uma vez ... int i; // estas duas linhas vão float x = 2, pot = 1; // no início da função "main" ... printf("+--------+--------+---------+\n"); printf("| x |log_2(x)| log(x) |\n"); printf("+--------+--------+---------+\n"); for (i=0; i<10; i++) { printf("| %6.0f | %6.3f | %6.3f |\n", x, f_logBase2(x,N), log(x)/LN2); x = pot * x + 13; if (i%3==0) pot = pot*2; } - Fazer um programa utilizando as funções acima para computar o logaritmo na base 2 para
vários valores digitados pelo usuário (
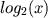 ).
).
O programa pára quando o usuário digitar algum valor menor que 1.
- Listar uma tabela na forma abaixo para verificar se sua função
"log" coincide com a função "log" da biblioteca C.