.: midpoint :.
midpoint:
Given two points A and B, the midpoint of AB
is the point M, from those that are equidistant of A and B the one least distant.
M : ||M-A|| = ||M-B|| and <||P-A|| = ||P-B|| => ||M-A|| <= ||P-A||>
Resume
The construction presented uses the construction of the
bisector
intercepting it with the segment AB.
Briefly the algorithm is:
Given the points A and B
1: s0:= Segment ( A,B )
2: c0:= Circumference ( A,B )
3: c1:= Circumference ( B,A )
4: C:= IntersectionPoint_south ( c0,c1 )
5: D:= IntersectionPoint_north ( c0,c1 )
6: s0:= Segment ( C,D )
7: M:= IntersectionPoint_south ( r,s0 )
Construction's details
The construction "usually" taught to the midpoint between A and B is the following:
- Build the segment AB;
- Build a circumference of arbitrary radius k centered
in A;
- Build a circumference of radius k centered in B;
- Take the points C and D of the intersection between both
circumferences and build the line CD;
- Take the intersection point between AB and CD. This is
the midpoint of the segment AB.
Although this algorithm to obtain the midpoint presents two "problems":
the first one is that it must be careful with the radius k, it must be
strictly bigger than half the distance between A and B,
but the "bigger" problem is that for it to work it is needed that the compass have "memory" (which is, the second
circumference must have precisely the same radius as the first one - "memorize" the radius of the first one).
To eliminate these problems one can apply the algorithm already shown to build the
bisector,
which considers the circumferences of center A and B, both with radius
||B-A|| (distance between A and B). See the details below:
- Given the points A and B, build the segment connecting them.
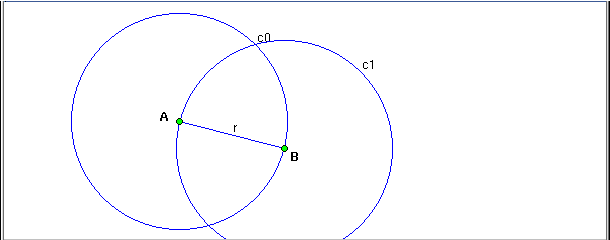
- Build the circumference c0 of center A, that passes by B, and also
the circumference c1 of center B, that passes by A.
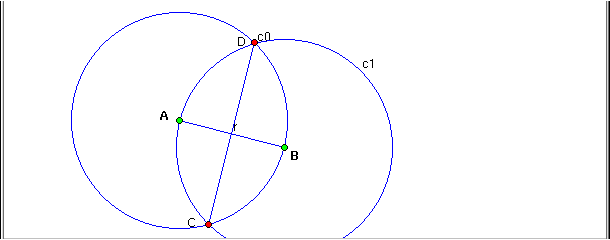
- Build the points C and D, intersections between c0 and c1.
Define the segment CD.
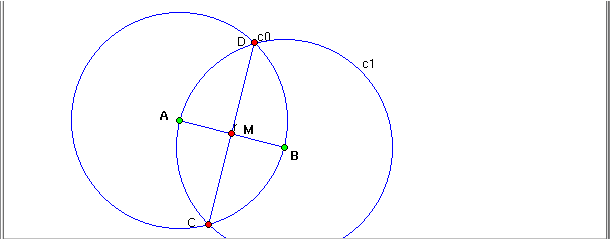
- Build the point M, intersection between the segments AB and CD.
This is the midpoint of AB.
Interactive construction
We present below the construction proposed above inside iGeom.
Move the point A (or B) and observe that the point M is always
equidistant of the points A and B.
To move a point, the button "move" must be selected
 .
.