.: Angle bisector :.
Angle bisector:
Ray that divides the angle in two even parts.
ray(O,C) : ang(BOC)=ang(COA)
Resume
We will build a angle bisector of an angle defined by the rays OA and OB,
as shown on the image below.
Briefly the algorithm is:
given the rays OA and OB
1: s0:= Ray ( O,A )
2: B:= Point ( 254.0,-145.0 )
3: s1:= Ray ( O,B )
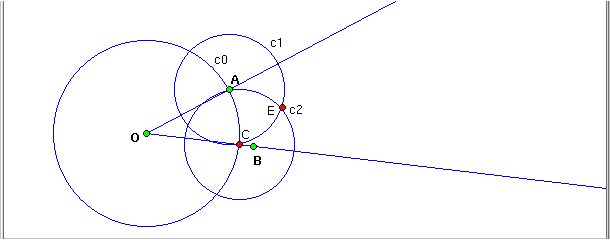
4: c0:= Circunference ( O,A )
5: C:= PointIntersection_south ( s1,c0 )
6: c1:= Circunference ( A,C )
7: c2:= Circunference ( C,A )
8: E:= PointIntersection_north ( c1,c2 )
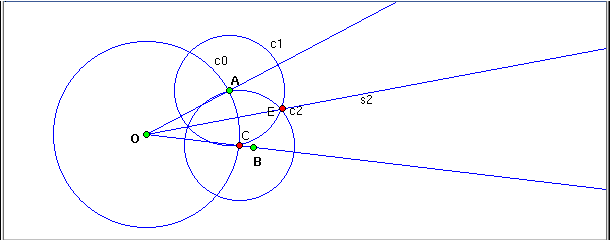
9: s2:= Ray ( O,E )
Construction's Details
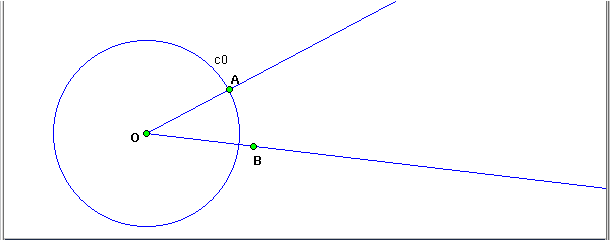
- Build the circunference c0 of center O that passes by A.
- Build the intersection point between c0 and the ray OB.
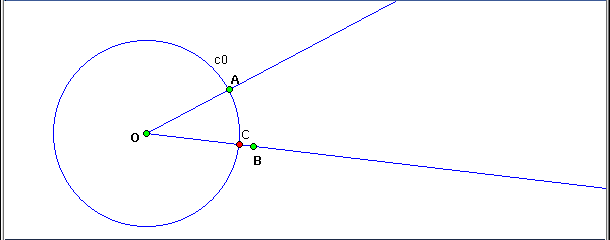
- Build the circunference c1 of center A that passes by C, and
c2, of center C that passes by A.
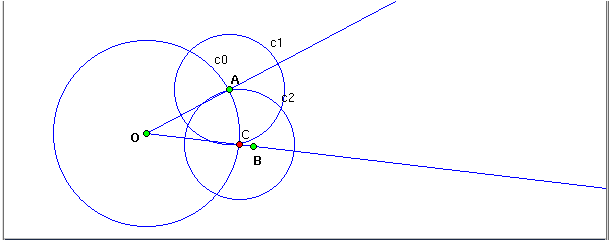
- Build the point E, intersection between c1 and c2.
- Build the ray OE, this ray represents the angle bisector.
Interactive construction
We present below the construction proposed above inside iGeom.
Mode the point A (or B, or O) and observe that the line s2, is always the angle bisector of AOB.
To move a point, the button "move" must be selected
 .
.