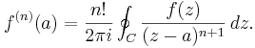
Descrição: Nesta disciplina estudaremos o plano complexo e as transformações que preservam a estrutura complexa do plano, as chamadas funções holomorfas. Estudaremos funções holomorfas usando ferramentas algébricas, analíticas e geométricas.

Os tópicos que abordaremos neste curso têm conexão com: Teoria de números, análise, sistemas dinâmicos, geometria, fractais, física-matemática, entre outros.

Conhecimento de cálculo diferencial e integral é altamente recomendado.

Aulas: Segunda e Quarta 15:30-17:30 na sala PC01 do Centro Politécnico.

ATENÇÃO: Na semana 23-27 de Maio, as aulas serão ministradas pelo Prof. Eduardo Hoefel.

Avaliação: Duas provas (P1,P2), cujas datas são:

Prova 1: 02/05/2011    (Tudo até índice de curvas).

Prova 2: 20/06/2011

Segunda Chamada: 22/06/2011

Exame Final: 04/07/2011

Além disso teremos listas de exercícios (L). A nota final será calculada da seguinte forma:

Nota Final= 0.4P1 + 0.4P2 + 0.2L

NÃO haverá prova substitutiva. A data da prova final será informada em breve.

Ementa: Estudaremos os seguintes tópicos:

1. 1. O corpo dos números complexos: Aspectos algébricos, topológicos e geométricos.
   

2. 2. Funções holomorfas: Séries de potências, Derivação de séries de potências, Equações de Cauchy-Riemann.
   

3. 3. Integração complexa: Integrais de linha, Índice de uma curva fechada, Fórmula integral de Cauchy, Teorema de Liouville, Teorema fundamental da álgebra.
   

4. 4. Propriedades de funções holomorfas: Derivadas de ordem superior, limite de sequências de funções holomorfas, princípio do módulo máximo.
   

5. 5. Singularidades: Zeros e pólos,  resíduos, singularidades essenciais e removíveis. Expansão em Séries de Laurent,Teorema de Casorati-Weierstrass.
   

6. 6. Aplicações Conformes: Transformações de Möbius, Lema de Schwarz, Automorfismos do disco, Teorema da aplicação de Riemann. Automorfismos conformes do anel.
   

7. 7. Aplicações: Dependendo do interesse dos alunos, poderemos estudar aplicações em: Teoria de números (Função Zeta de Riemann, funções elípticas, formas modulares), Sistemas dinâmicos (conjuntos de Julia e Fatou), Exemplos de superfícies de Riemann.
   

Bibliografia:

1. 1.  J. Conway: Functions of one complex variable, Springer Verlag.
   

2. 2.  W. Rudin: Real and complex analysis, McGraw-Hill 2a. Edição.
   

3. 3.  L. Ahlfors: Complex Analysis, McGraw-Hill, 3a. Edição.
   

4. 4.  R. Churchill: Complex variables and applications, McGraw-Hill.
   

Notas:

Estão disponíveis as notas sobre singularidades de funções. Podem acessar o arquivo pdf no link singularidades.pdf 

Listas:

1. 1.  Lista1.pdf  (Entregar dia 16/03 no horário da aula)
   

2. 2.  lista2.pdf   (Entregar dia 11/04 no horário da aula)
   

3. 3.  Lista3.pdf  (Não precisa ser entregue)
   

4. 4.  Lista4.pdf
   

The Chess board after applying a conformal map!

Veja o link para mais informação sobre aplicações conformes!