|
|
CapXIV-pg5 |
|
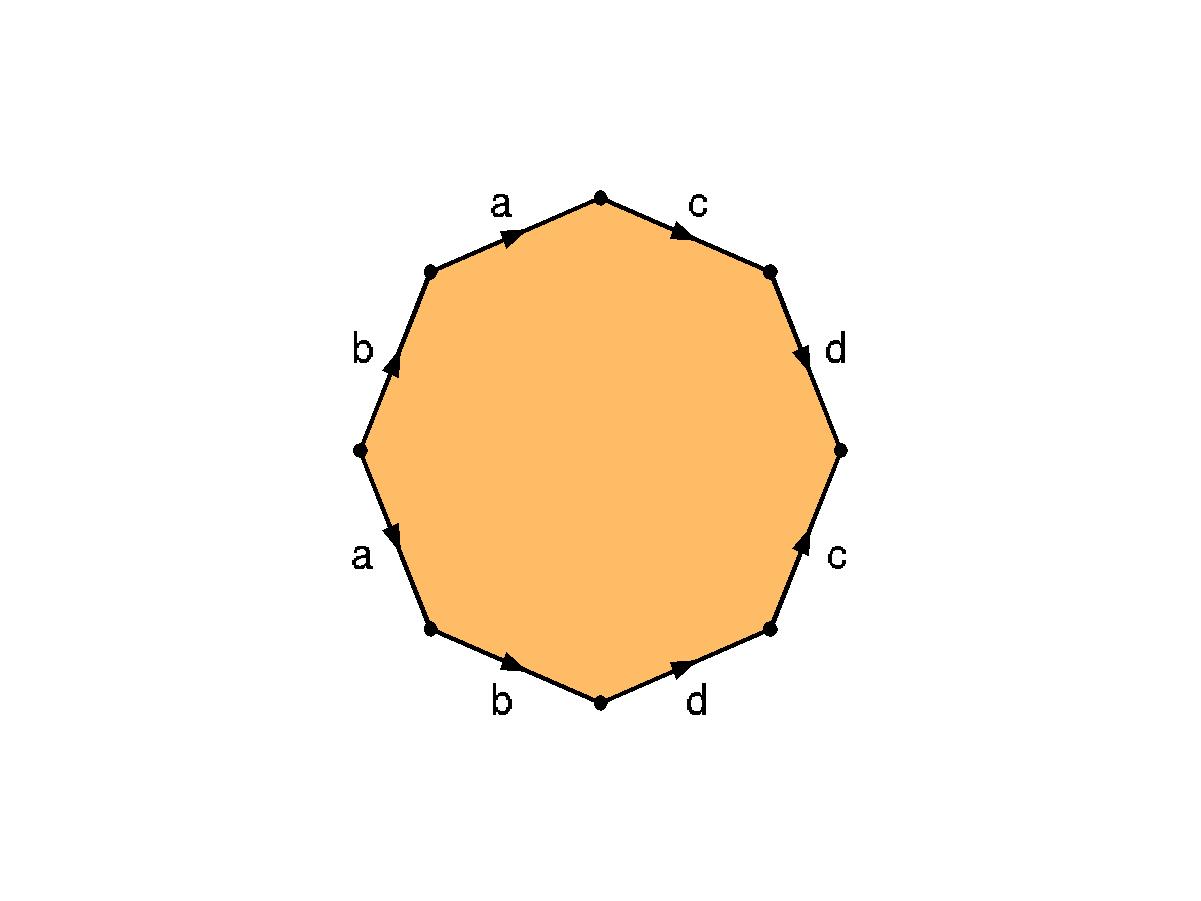
Ou seja, o bitoro pode ser definido através da identificação dos lados de um polígono de 8 lados (um octógono). |

|
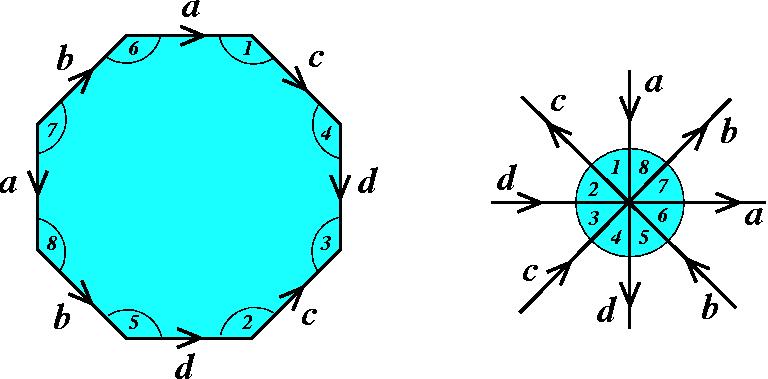
Note que, assim como no toro, todos os vértices desse polígono representam um ponto só do bitoro, após a identificação. Sua vizinhança aparece dividida em oito pedaços no polígono. A figura abaixo mostra como se "recompõe" a vizinhança desse ponto. |
|
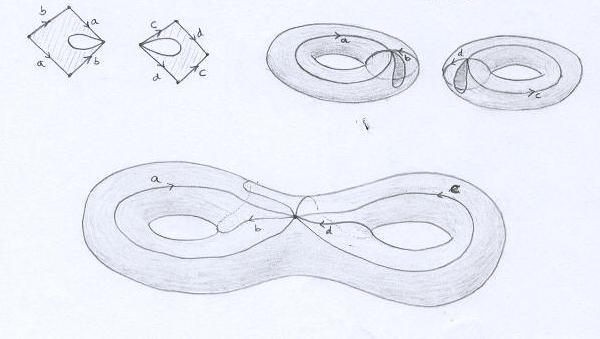
Se todos os vértices do polígono representam o mesmo ponto do bitoro, então cada segmento que une esses dois vértices é uma curva fechada! Por exemplo, as quatro curvas a, b, c e d podem ser reconhecidas no bitoro. |
|
A construção do bitoro sugere uma maneira de se fazer qualquer soma conexa usando-se modelos poligonais, que ilustramos com a seqüência de figuras abaixo. |
|
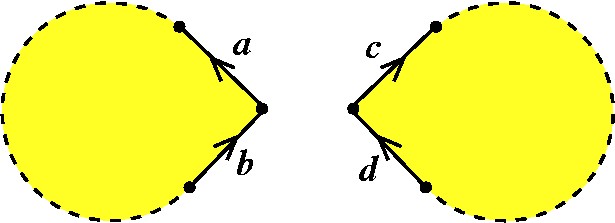
Esta é a situação inicial, com as duas superfícies que queremos somar. As linhas pontilhadas representam as arestas dos modelos poligonais que não nos interessam aqui. Usaremos desse recurso sempre que quisermos mostrar que uma afirmação vale em geral, e não somente para modelos particulares. |
|
|
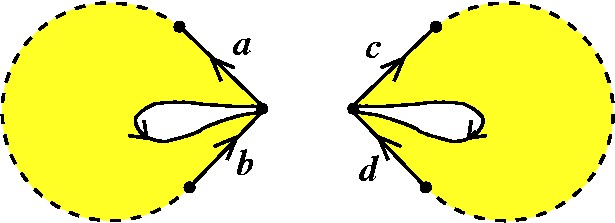
Para fazer somas conexas, temos que remover uma tampa de cada superfície. Fazemos isso de tal forma que o bordo da tampa toque um vértice (no caso, o vértice entre as duas arestas explicitadas nos modelos). Além disso, como colaremos as superfícies pelos bordos das tampas, colocamos uma orientação nos bordos que servirá de guia para a colagem. |
|
|
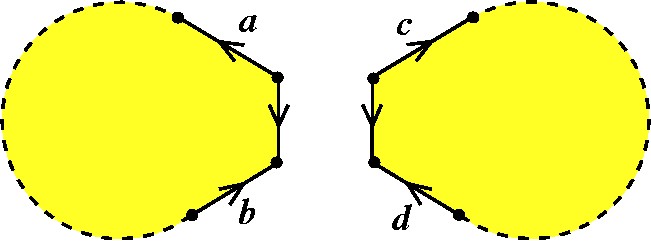
A próxima etapa é cortar cada modelo pelo vértice onde encosta o bordo da tampa, fazendo com que cada um deles passe a ter uma aresta a mais. |
|
|
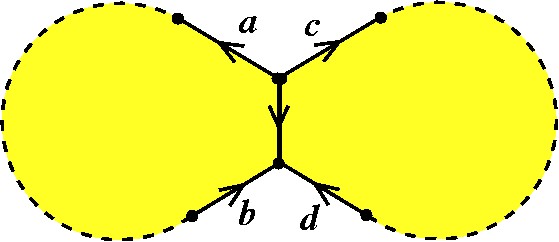
Então fazemos a colagem, como planejado... |
|
|
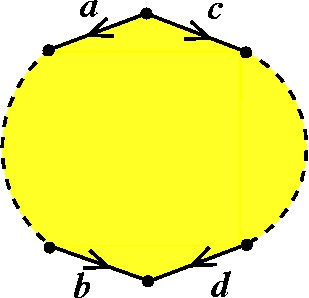
...e deformamos o modelo, para ficar numa forma mais natural. Pronto! Ficamos com um novo modelo poligonal, que é o modelo da superfície resultante! |
|
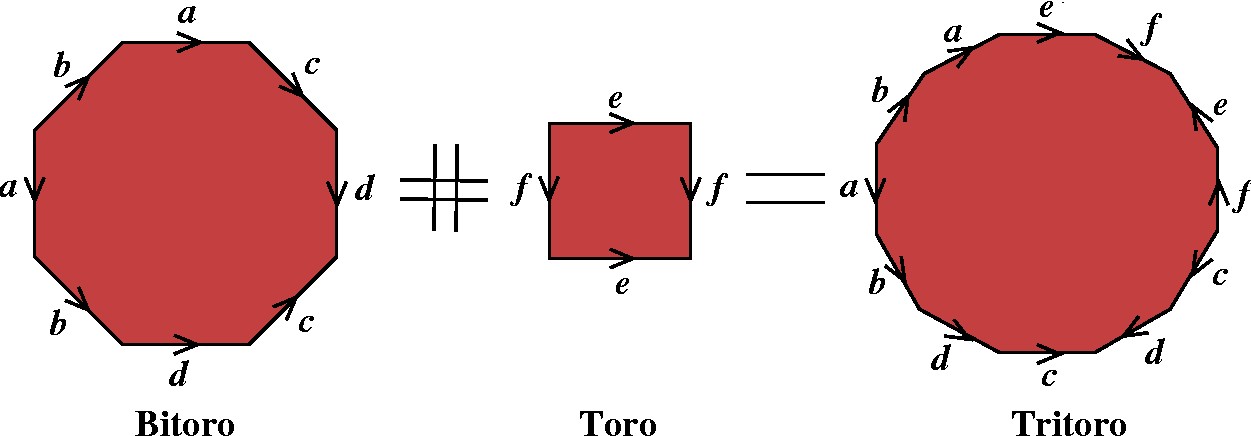
O Tritoro, para exemplificar, também é produzido por soma conexa, neste caso do Bitoro com o Toro. |
|
|
CapXIV-pg5 |
|