
NEW CHAP. 5 OF THE PAPER ON ALGORITHMS BY V.W.SETZER AND
F.CARVALHEIRO
V.W.Setzer
Version 2.0 of Jan.29, 2002
5. A more efficient method
This chapter, written by V.W.Setzer, is different from the corresponding one in the original paper. Instead of illustrating a more efficient method using the tree sort method, it uses binary merge sort. The suggestion for the use of this other method, much simpler and illustrative, even a little more efficient, was given us by Prof. Michael Schrefl, of the Johannes Keppler Universität, Linz, Austria. Click here for the paper with the original chapter.
5.1 Motivation
The instructor tells that his manager will probably say: "Your friends took 30-40 minutes to reach these solutions. If they would work for a whole morning, would they come up with a more efficient solution?" He asks the participants what they think about this question. In general, most of them think it is possible to obtain a better method, but there are always some that think no better method can exist.
A much more efficient method, binary merge sort, is then introduced. We will present it here in a way that at least part of the students may participate in the process, doing something with their bodies and hands. This way, it illustrates in a live way the process for the rest of the class. In section 5.6 we present two variations; in one of them one may have a similar situation to the other methods already seen, that is, using cardboards.
5.2 Preparation
A student is called to the front of the classroom, staying just ahead the blackboard looking at the class, at about the middle of the class width. The instructor gives that student a shuffled pile of 8 cards; each card has a number written on it. The class is told that the student is too lazy to sort the pile. Thus, she needs 2 assistants. The student may choose those 2 assistants among her classmates. The instructor positions those 2, looking at the class, ahead of the first, forming a new row (the second, if we consider that the first student forms a row by herself), so that each one of them divides, in about two equal parts, each half of the width of the class, according to fig. 4.

fig. 4
The first student, being lazy, passes the task of ordering her pile to her 2 colleagues, distributing an equal number of cards among them, that is, a pile of 4 cards for each one. Then she waits for them to sort their piles. It happens that those 2 students are also lazy, so that each one is going to call 2 assistants. Those new 4 are positioned ahead of the second row, forming a third one, each one dividing 1/4 of the width of the room more or less in two, according to fig. 5.
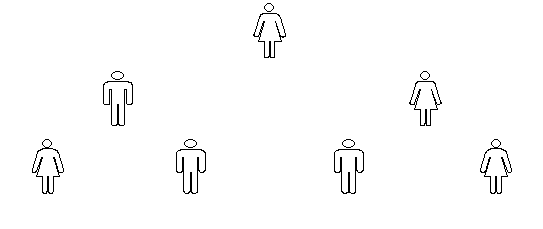
fig. 5
Each student at the second row divides her pile of cards equally among her assistants, each one of them receiving 2 cards. Those are also lazy, so each one calls, two new assistants, forming a fourth row with 8 students. Each student of the third row distributes her two cards for each one of her assistants, that is, a card for each one. Fig. 6 shows that situation with the value of each card being hold by each student of the last row.
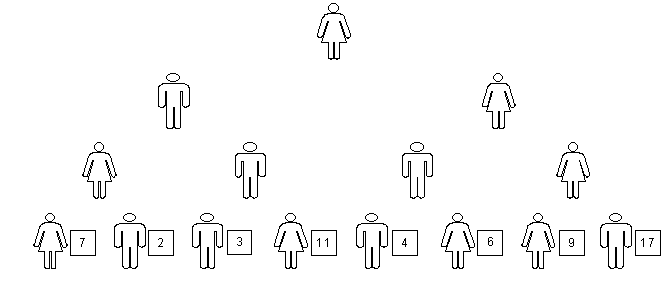
fig. 6
The instructor draws this figure on the blackboard, including the value of the cards of the last row. He then says that this structure, used quite frequently in computer science, is denominated a tree, here a "tree of people"; he observers, for example, that as the computer programmers and scientists are very funny people, seeming to speak a language of another world, they draw their trees upside down. He writes on the picture the usual denominations: each row is called a tree level; each element of the tree is called a node; each node of the last level (in our example, with 8 students) is a leaf; the node of the first level (with just one student) is the root of the tree; each node excluding the root has just one father node on the previous level, and each node excluding the leaves has exactly two sons in the next row, thus characterizing this data structure as a binary tree. The height of the tree is the number of its levels, that is, the number of nodes that may be visited travelling from the root to a leaf, always in the direction of the sons (in our example, the height is 4).
It is important to show that the tree is formed using a uniform rule: each student builds the part of the tree corresponding to her 2 sons, and passes half of her pile to each one. This happens with all levels, excluding the level of the leaf nodes, for they have just received one card each, so they cannot divide their (unitary) pile in 2. This signals the end of the construction of the tree.
5.3 Sorting
After the tree of students has been built, we proceed to the sorting phase. Each student of the next-to-last (third) row, one at a time, from the left of the room to the right, turns her assistants to herself, and examines their cards. She grabs the card with the smallest value (or the one that is to her right, if they have the same value), maintaining it with the face upward, and then the one with larger value (or the other, if they have the same value). She places the latter underneath the previous one, also with the face upward. Then she turns her assistants again to the class, showing the latter her pile with the cards a little shifted, so the class may see their values. The instructor copies those values in the corresponding node on the tree at the blackboard. When all the students of the third row have finished doing this, we will have 4 ordered piles of 2 cards each, as in fig. 7.
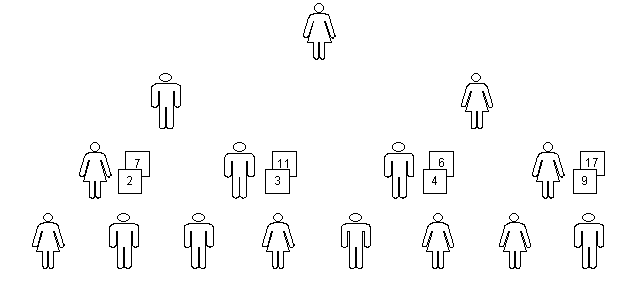
fig. 7
Each student of the second row turns her assistants to herself and takes one card from one of them at a time, merging the cards in increasing order of value (or in non-decreasing order, if there are cards with equal values). For this, she examines every time the upper cards of her assistants' piles and fetches the one with the smallest value, placing it under the card that was fetched before, if there is one. It would be interesting to tell the class which cards are in the upper position of her assistantsí piles. When a card is removed from an assistant, the next card appears, and is used for the next comparison, until there are no more cards with one of the 2 assistants. The instructor should notice to the class that, for each student of the second row, the last card that remains with an assistant is not compared to another card, because the other assistant no longer has any card. This last card may be immediately moved to the end of the pile. After the pile of a student of the second row is ready, her assistants turn again to the class and the resulting pile is shown to the class; the instructor copies the values in the corresponding node on the blackboard. When there is no more card in the third row, each one of the two students in the second row has a pile of 4 cards, ordered in increasing order, as in fig. 8.
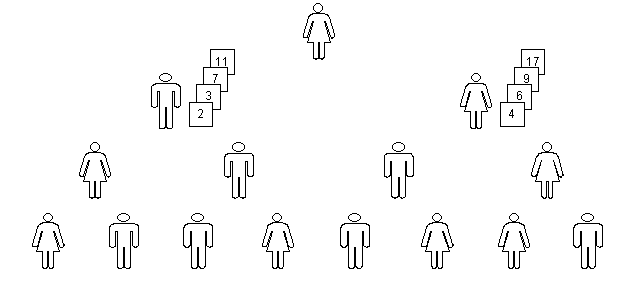
fig. 8
The student of the first row (the one at the root node) turns his assistants to himself, and begins to fetch their cards, merging them in the same way as each student of the second row fetched cards from her assistants. The instructor notices again that the last card that remains with one of the assistants is not compared, being simply moved to the end of the pile that is being constructed by the student at the root. The assistants turn to the class. At the end of that process, the student of the root has a pile of sorted cards in increasing order. She holds the cards a bit shifted, and shows her piles to the class. The instructor copies them in the picture at the blackboard, at the root node of the tree, as in fig. 9.
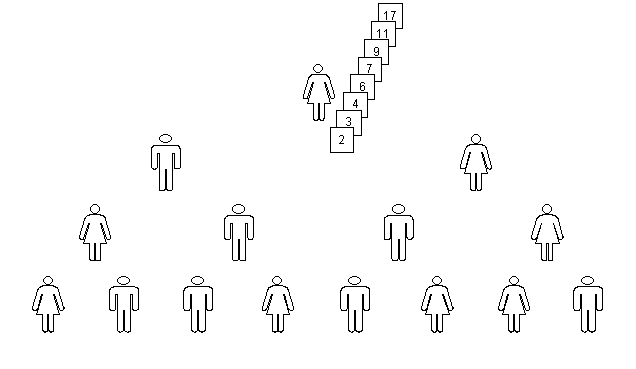
fig. 9
Again, it is important for the instructor to call the attention to the uniformity of the process: each student merges the cards of her two assistants. In the case of the students in the third row, there is also a merging process, reduced to a trivial case, because each one of their assistants has just one card. In this case there is only one comparison, followed by the movement of the card with the smallest value and, at last, the simple movement of the last card, as in the intermediate nodes. The sorting process finishes when the student of the root node has finished merging all of his assistants' cards.
The instructor asks the students of the tree to sit down, and starts to use the picture at the blackboard in the following explanations, always trying to remind the students what happened in the real tree. Another possibility is to send the students of each row to their seats as soon as there is no more cards in that row, or even each pair of assistants as soon as their cards have all been moved. This way the merging processes become more visible.
5.4 Calculating the time complexity
For the calculation of how many comparisons are necessary to sort n numbers with this method, we will ignore the construction of the tree, because it doesn't require any comparison at all and, as we will see on 5.6, it is not even necessary. Let us proceed, therefore, to the sorting phase.
Let us remember that, for each student of a row, each card that she removes from an assistant and places in her pile is compared with the topmost card of the other assistant's pile, except for the last card. As we pointed out above, the latter is placed without comparison under her pile (since the other assistant's pile is now empty). The instructor calls the attention to the fact that this is the worst case, since it may happen that of one of the assistants gets without cards and the other has still 2 or more cards. In this case, there will be 2 or more comparisons less. It would be interesting to give an example, as for instance the extreme case of the assistantsí piles containing 1-2-3-4 and 5-6-7-8 respectively. Here there would be 4 comparisons (by construction, each pile is ordered, so that when the first pile is finished, it is enough to consecutively move each card from the other pile), instead of 7, corresponding to the worst case. Therefore, considering all the students of a row, in the worst case the number of comparisons is the total number of cards minus the number of students of the row (because there will be, for each student, one comparison less than the total number of cards in the its assistants' two piles).
The instructor constructs at the blackboard, at the side of the example tree, a table whose lines should be in parallel with the levels (rows) of the tree, with 3 additional last lines as below. The second column indicates how many nodes exist in each level, and the third column how many comparisons are made in each level. The generalization of the last 3 lines should be carefully explained.
|
Level |
Nodes |
Compar. |
|
0 |
1 |
n-1 |
|
1 |
2 |
n-2 |
|
2 |
4 |
n-4 |
|
3 |
8 |
n-8 |
|
... |
... |
... |
|
m-1 |
2m-1 |
n-n/2 |
|
m |
2m |
n-n=0 |
Therefore, the total number of comparisons C is given by the sum of all the terms of the last column, less the one of the last line, that is, up to line m-1:
C = (n-1) + (n-2) + (n-4) + (n-8) + ... + (n-n/2)
As there are m terms to be added (counting from 0 to m-1, in the leftmost column),
C = mn - (1 + 2 + 4 + 8 + ... + n/2)
The instructor observes that the second term of the last formula indicates the total number of nodes of a binary tree with n/2 leaves. Showing several levels of the tree at the blackboard, he observes that, if some level of any binary tree has k nodes, the total number of nodes from the root to that level is always 2k-1. This can be easily proven by finite induction on the number of levels m, but if the students don't know proofs by induction, this would be too much. Thus,
C = mn - 2(n/2) - 1
It remains to calculate m, which corresponds to the level number of the leaves (or the height of the tree minus one). But, by construction, the number of nodes in the level of the leaves is the number n of values we want to sort. Observing the table, we have
2m = n
which can be seen in the example tree (for m=3, 2m=23=8). Taking the base 2 logarithm of both sides,
log22m = log2n
mlog22 = log2n
m = log2n
It is interesting to observe that this formula permits the calculation of the height m+1 of a given binary tree given its number of leaves n.
Therefore, the total number of comparisons in the worst case will be
C = nlog2n - n + 1
It is important to observe that this formula is valid for n equals to a power of 2. If n is not a power of 2, it is always possible to complete the leaves that would be empty, placing in them a number larger than any of the values to be ordered (that is, playing the role of infinite). After sorting the cards, those that contain this number will be at the end of the pile and should be removed. Thus, for certain integer positive values n and m such that 2m-1<n<2m, one should take m for the calculation of the number of comparisons.
5.5 Comparison with quadratic methods
The table below shows, for the worst cases, the number of comparisons for the quadratic and binary merge methods:
|
n |
n(n-1)/2 |
nlog2n - n + 1 |
|
1 |
0 |
0 |
|
2 |
1 |
1 |
|
4 |
6 |
5 |
|
8 |
28 |
17 |
|
16 |
120 |
49 |
|
32 |
496 |
129 |
|
64 |
2.016 |
321 |
|
128 |
8.028 |
769 |
|
256 |
32.640 |
1.793 |
|
512 |
130.816 |
4.097 |
|
1024 |
523.776 |
9.217 |
|
2048 |
2.096.128 |
20.481 |
|
4096 |
8.386.560 |
45.057 |
|
8192 |
33.550.336 |
98.305 |
It would be interesting for the instructor to call the attention to the fact that in the quadratic method, in the limit there are n2 comparisons (represented as O(n2), read "of the order of n2"), that is, as the number of elements doubles for each new row, the number of comparisons practically quadruplicates. In the binary merge method at the limit one has nlog2n comparisons (represented as O(nlog2n)); as the logarithm is a function that tends to increase very little with the increase of its argument, the tendency is the number of comparisons almost doubling when doubling the number of values to be sorted. This can be seen in the table above.
The instructor should also call the attention to the enormous difference of efficiency between the methods. Phonebooks represent an interesting real example, because they have to always be sorted for each new edition, supposing that new subscribers are placed initially at the end of the previous list. For a list with 131,072 subscribers, we have 8,589,869,056 and 2,097,153 comparisons for the two methods, respectively, For 1,048,576 subscribers, we have 549,755,813,888 and 19,922,945 comparisons. In a computer that makes 1,000,000 comparisons per second, we have in the worst cases for this last example a time for the execution of the programs (taking into account just the comparisons!) of approximately 6 days and 19 seconds, respectively.
An interesting comparison is the fact that the quadratic methods didn't need auxiliary storage space, that is, additional intermediary compartments. In the case of the binary merge method where the whole tree is constructed, as presented above, it is necessary to use n-1 auxiliary nodes (students), that is, the number tree nodes excluding the leaves. But as each intermediate students holds more than one card, it is in fact necessary to have n auxiliary storage positions per level. Thus, the number of additional storage positions will be (m-1)n. This is a great inconvenience of this method. In the next section we will se a variation where only n additional positions are necessary.
5.6 Possible variations
Instead of building the tree in the way shown above, that is, giving the initial shuffled pile to the root student, and continuing as described, the tree can be built without the piles of cards. After its construction, the shuffled cards may be distributed to the leaf students of the tree. One proceeds with section 5.3.
Still another possibility is to build just the leaf nodes, distributing a card to each student. Then the next row is built, the leaf cards are merged as indicated, then another row is built, etc. Thus, the tree nodes are built only when necessary.
>Instead of building a tree, it is possible to use just two rows A and B of 8 students each, facing each other. As an example, for the case of 8 cards let us call A1 to A8 the students of row A, and B1 to B8 the ones of B, in such a way that A1 is in front of B1, etc. The idea is to merge cards from 2 groups of students in one row, moving these cards to the 2 parallel groups of students in the other row, always one card per student. After having moved all the cards from one row to the other, the number of students in each group is doubled before starting the merge process again. In the beginning, the merge is done between 2 groups of 1 student each (that is, between A1 and A2, between A3 and A4, etc., with the merged cards moved to B1 and B2, B3 and B4, etc., respectively). Then with 2 groups of 2 students each (between B1, B2 and B3, B4, then B5, B6 and B7,B8), and finally among 2 groups of 4 students (between A1 to A4 and A5 to A8). For this, one may use a student who executes the comparisons and the movements of the cards. It is also possible to use students that work as "pointers", two of them indicating with a finger which elements of each group should be compared next, let us say on row A, and another one indicating to which student of the other row, B in this case, the next card should be moved.
In this second method, it is necessary to use an auxiliary storage space of n elements. It may also be implemented with cardboards, with two lines of pockets, instead of using students. This would give all the students in the class the opportunity of participating, as we have seen with the quadratic methods. When using cardboards, it is interesting to add an additional rule to the R1 to R5 rules introduced in the quadratic methods:
R6. The use of additional pockets is permitted; they follow the rules R1 to R5.
A slight modification of the last variation can be suggested: in fact, it is only necessary to use n/2 auxiliary storage pockets. When merging the leaf nodes (level m, merging groups of 1 node) and constructing level m-1, it is eventually necessary to exchange 2 consecutive nodes, so no auxiliary pocket is really necessary. For the step corresponding to constructing level m-2 (groups of 2), it is necessary to use just 4 auxiliary pockets (one of them was used in the previous level), used for all pair of groups. For each pair of groups, after merging its elements the result is moved to the original pockets (corresponding to the leaves). When merging the pockets corresponding to level 2 (groups of n/4), it is necessary to use just n/2 auxiliary pockets. The last merge, corresponding to elements of level 1, is done using only the original pockets.
It is possible to do a binary merge sort just using only the n original compartments; algorithms which use the same original space, plus some constant space for counters, pointers, etc. are called in-place merging algorithms. Let us present here a simple algorithm of this kind, requiring more comparisons. Let us suppose that two already sorted groups of elements G and B are being merged. If the examined element of G is larger than the examined element of H, they should be interchanged. The new element of G is necessarily smaller than the remaining elements of that group, but the same doesn't happen with the new element of H. In this case, it should be moved to its correct position in H, in order to preserve its ordering. For example, let us suppose that in the case of 8 values to be sorted one has arrived to the following two groups of 4 elements:
1-3-6-7#2-4-5-8
The following steps would be:
1-2-6-7#3-4-5-8; 1-2-3-7#6-4-5-8; 1-2-3-7#4-6-5-8; 1-2-3-7#4-5-6-8; 1-2-3-4#7-5-6-8; 1-2-3-4#5-7-6-8; 1-2-3-4#5-6-7-8
It is easy to verify that if there are two groups of k elements to be merged, in the worst case there will be 2k-1 comparisons for the merges (as it has already been seen), plus k(k-1) for the displacements (for example, in the extreme case of the groups 5-6-7-8#1-2-3-4). That second term turns the method a quadratic one - actually, of the order of O(n2log2n).
The instructor may tell the class that there exist in-place sort methods, like Quicksort (see, for example, [2]) - which is not of the class of merge sort algorithms -, of order O(nlog2n), that don't need variable auxiliary space (actually, Quicksort needs space to keep the recursion stack or, if the recursion is eliminated, a stack substituting the recursive call that is not of the "tail recursion" type; the extra space required for the stack is of the order of O(log2n)) [2]).