Análise de três ou mais variáveis
Variáveis Categóricas
require(gtsummary)
mtcars %>% select(vs,am,gear) %>%
mutate(vs=ifelse(vs==0,"V-Shaped Engine","Straight Engine"),
am=ifelse(am==0,"Automatic","Manual")) %>%
tbl_strata(
strata = vs,
.tbl_fun =
~ .x %>%
tbl_cross(gear, am, margin = NULL)
)|
Straight Engine
|
V-Shaped Engine
|
|||
|---|---|---|---|---|
| Automatic | Manual | Automatic | Manual | |
| gear | ||||
| 3 | 3 | 0 | 12 | 0 |
| 4 | 4 | 6 | 0 | 2 |
| 5 | 0 | 1 | 0 | 4 |
Variáveis Categórias e Quantitativas
require(GGally)
mtcars %>% select(mpg,disp,hp,vs,am) %>%
mutate(vs=as.factor(vs),am=as.factor(am)) %>%
ggpairs(.,mapping=ggplot2::aes(colour=am),
lower=list(continuous=wrap("smooth",alpha=0.3,size=0.1)))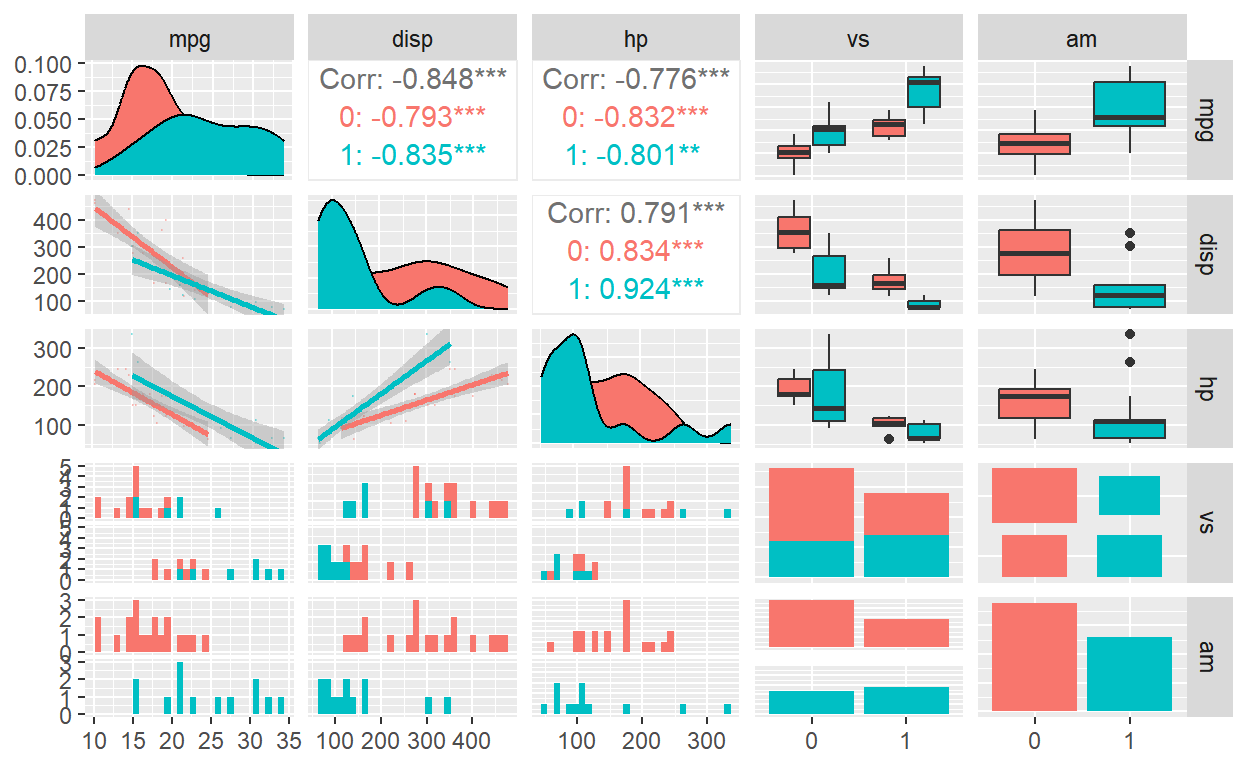
- Outros Exemplos
- Veja também a biblioteca
esquissedo R!
Simulação
Lei dos Grandes Números (LGN)
Seja \(X_1, X_2, \ldots\) uma sequência de variáveis aleatórias independentes e identicamente distribuídas (i.i.d.), com \(Var(X_1)<+\infty\). Então, \[\frac{1}{m}\sum_{i=1}^mX_i ~~\xrightarrow[m\rightarrow\infty]~~ E[X_1]~.\]
Exemplo 1: \(X \sim Bernoulli(p)\)
\(P(X=1) = p\); \(P(X=0) = 1-p\); \(E[X] = P(X=1) = p\).
Considere \(p=0.6\).
set.seed(666)
m=20; p=0.6
x <- rbinom(m,1,p)
media = cumsum(x)/seq(1,m)
amostra <- tibble(size=seq(1:m), x=x, xbar=media)
amostra # A tibble: 20 × 3
size x xbar
<int> <int> <dbl>
1 1 0 0
2 2 1 0.5
3 3 0 0.333
4 4 1 0.5
5 5 1 0.6
6 6 0 0.5
7 7 0 0.429
8 8 1 0.5
9 9 1 0.556
10 10 1 0.6
11 11 0 0.545
12 12 1 0.583
13 13 1 0.615
14 14 1 0.643
15 15 1 0.667
16 16 0 0.625
17 17 1 0.647
18 18 0 0.611
19 19 1 0.632
20 20 1 0.65 amostra %>% ggplot() + theme_bw() + guides(color="none") +
geom_line(aes(x=size,y=xbar,color=size), size=2) +
geom_point(aes(x=size,y=x,color=size)) +
geom_hline(yintercept=p)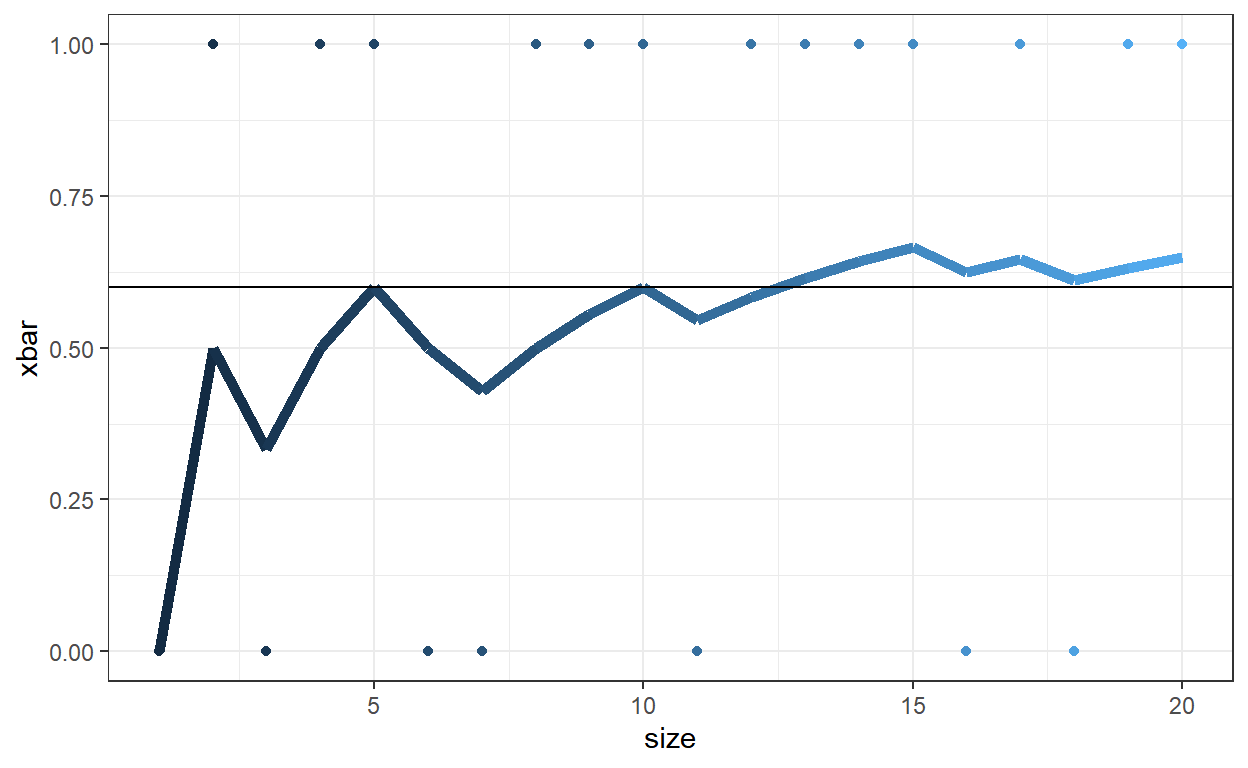
set.seed(666)
m=200; p=0.6
x <- rbinom(m,1,p)
media = cumsum(x)/seq(1,m)
amostra <- tibble(size=seq(1:m), x=x, xbar=media)
amostra %>% ggplot() + theme_bw() + guides(color="none") +
geom_line(aes(x=size,y=xbar,color=size), size=2) +
geom_point(aes(x=size,y=x,color=size)) +
geom_hline(yintercept=p)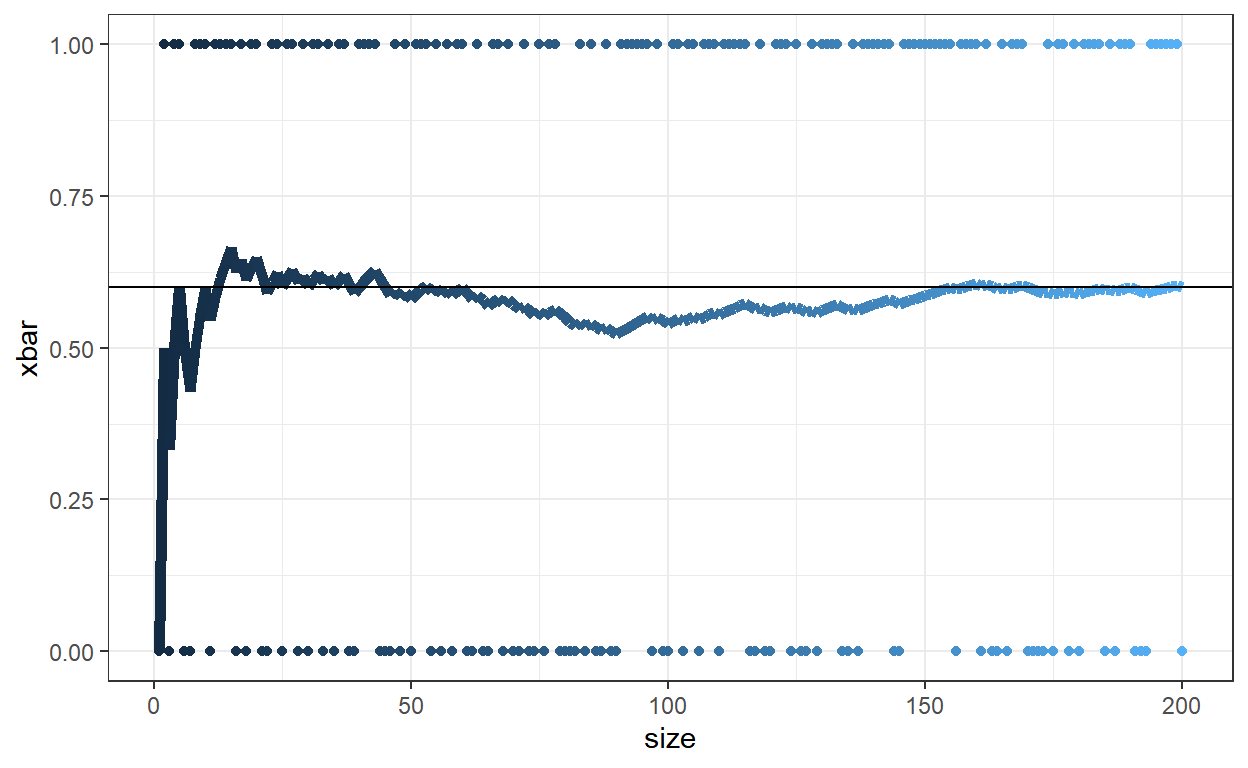
Exemplo 2: \(X \sim Binomial(n,p)\)
- \(P(X=x)= {n\choose x}~p^x~(1-p)^{n-x}\), \(E[X] = np\) e \(Var(X)=np(1-p)\).
set.seed(666)
m=300; p=0.6; n=10
# np=6 ; np(1-p)=2.4
x <- rbinom(m,n,p)
media = cumsum(x)/seq(1,m)
var = cumsum(x^2)/seq(1,m) - (media)^2
amostra <- tibble(size=seq(1:m), x=x, xbar=media, var=var)
amostra %>% ggplot() + theme_bw() + guides(color="none") +
geom_line(aes(x=size,y=xbar,color=size), size=2) +
geom_hline(yintercept=n*p)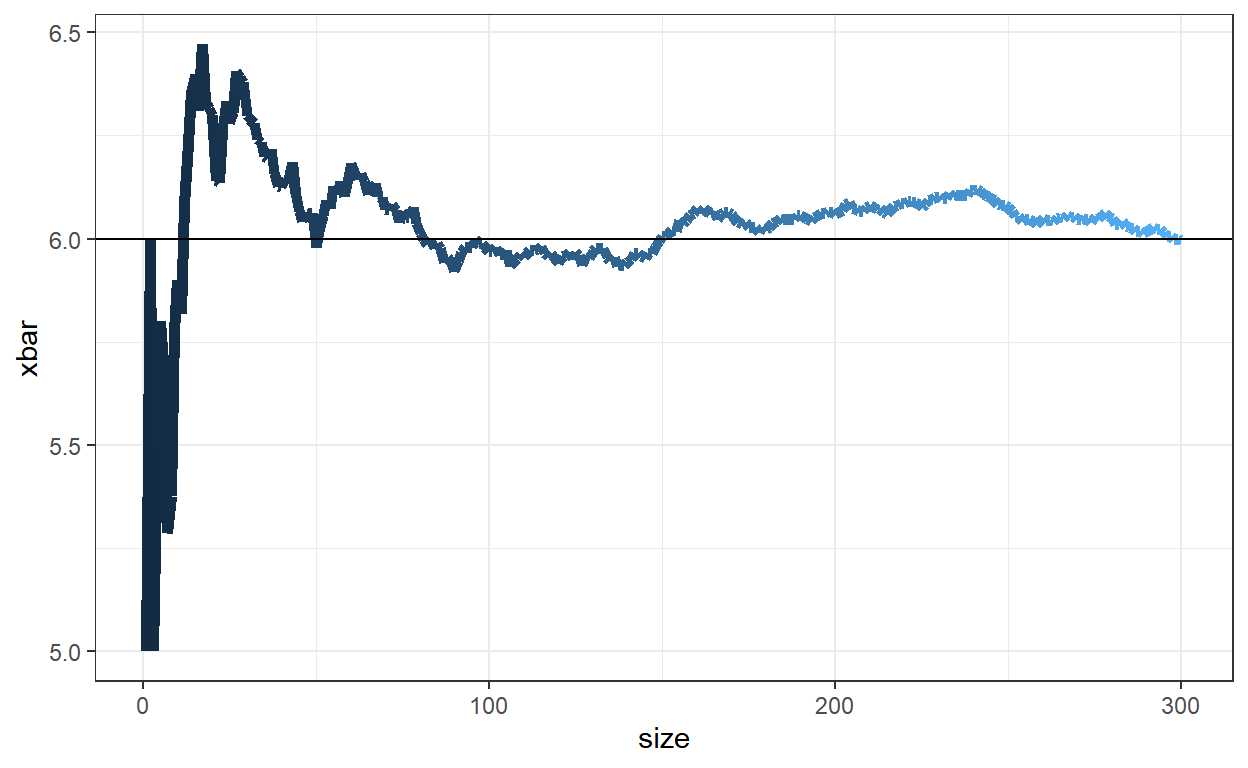
amostra %>% ggplot() + theme_bw() + guides(color="none") +
geom_line(aes(x=size,y=var,color=size), size=2) +
geom_hline(yintercept=n*p*(1-p))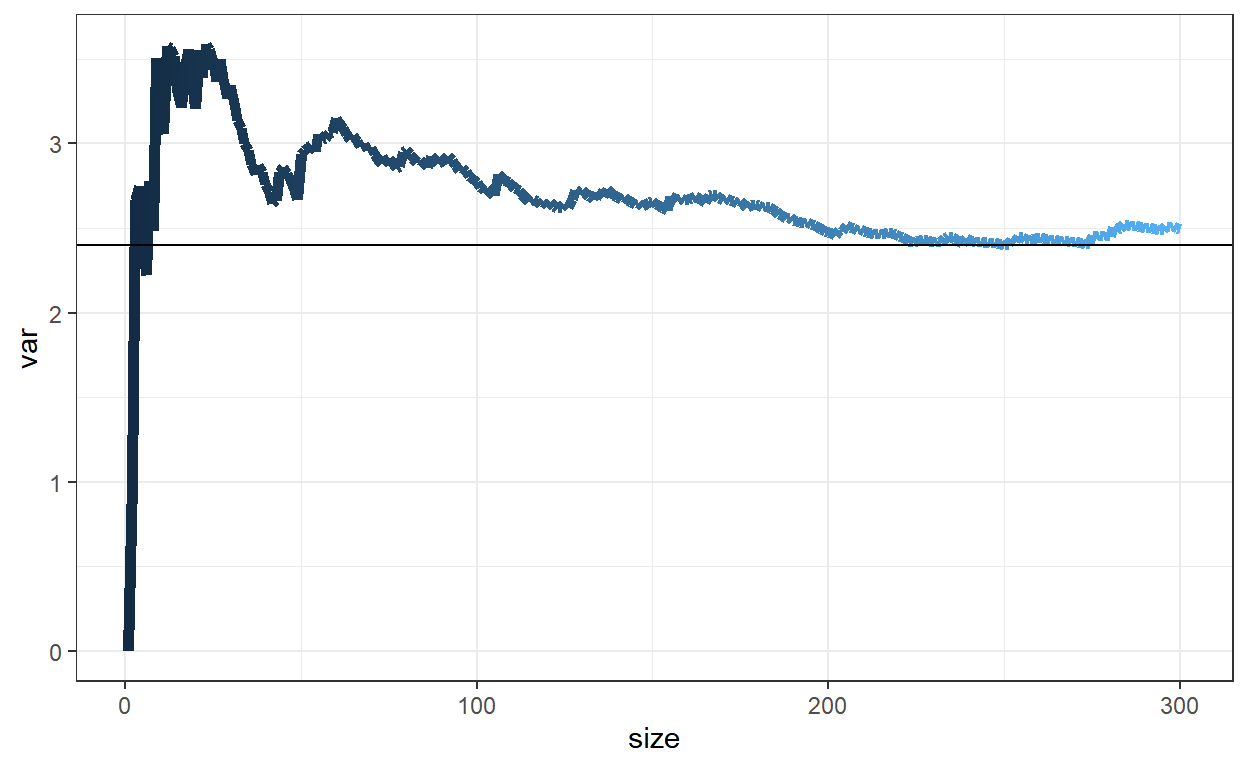
Pela LGN, \(\displaystyle \frac{1}{m}\sum_{i=1}^{m}\mathbb{I}(x_i=x)~~\xrightarrow[m\rightarrow\infty]~~ P(X=x) = E\left[\mathbb{I}(X=x)\right]\), para \(x\in\{0,1,\ldots,n\}\).
Então, pode-se aproximar a distribuição binomial pelas frequências relativas observadas na amostra.
set.seed(666)
m=1000; p=0.6; n=10
# np=6 ; np(1-p)=2.4
x <- rbinom(m,n,p)
teorica <- tibble(x=seq(0,n),Prob = dbinom(x,n,p))
amostra <- tibble(x=x) %>% group_by(x) %>%
summarise(FreqRel = n()) %>%
mutate(FreqRel = FreqRel/sum(FreqRel))
left_join(teorica,amostra,by="x") %>%
ggplot() + theme_classic() + xlab("") + ylab("P") +
ggtitle("Amostra gerada da Bin(n,p)") +
xlim(0-0.5,n+0.5) +
geom_col(aes(x=x, y=FreqRel),
color="black", fill="lightgreen") +
geom_point(aes(x=x, y=Prob), color="red", size=2)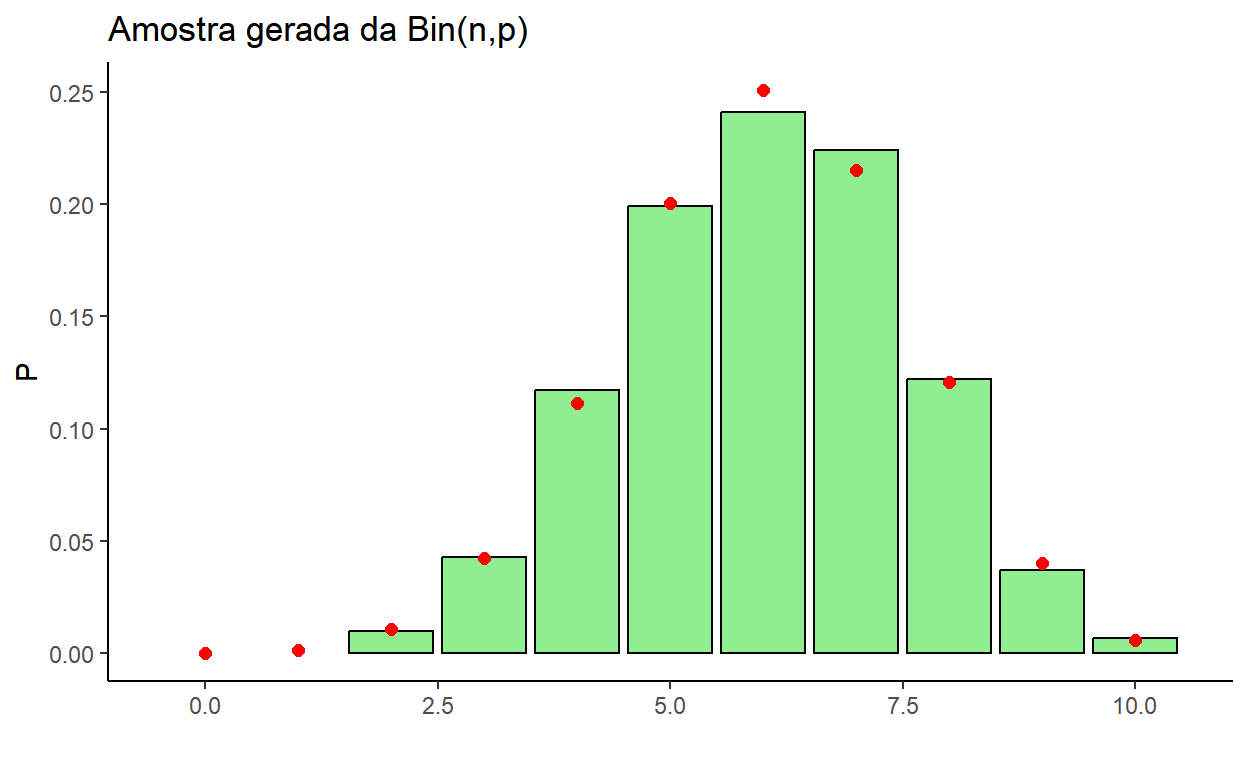
Exemplo 3: \(X \sim Poisson(\lambda)\)
- \(P(X=x)= \frac{\lambda^x~e^{-\lambda}}{x!}\), \(E[X]=Var(X)=\lambda\).
set.seed(666)
m=2000; lambda=13
x <- rpois(m,lambda)
teorica <- tibble(x=seq(0,max(x)+1),Prob = dpois(x,lambda))
amostra <- tibble(x=x) %>% group_by(x) %>%
summarise(FreqRel = n()) %>%
mutate(FreqRel = FreqRel/sum(FreqRel))
left_join(teorica,amostra,by="x") %>%
ggplot() + theme_classic() + xlab("") + ylab("P") +
ggtitle("Amostra gerada da Poisson(lambda)") +
xlim(0-0.5,max(x)+1.5) +
geom_col(aes(x=x, y=FreqRel),
color="black", fill="lightgreen") +
geom_point(aes(x=x, y=Prob), color="red", size=2)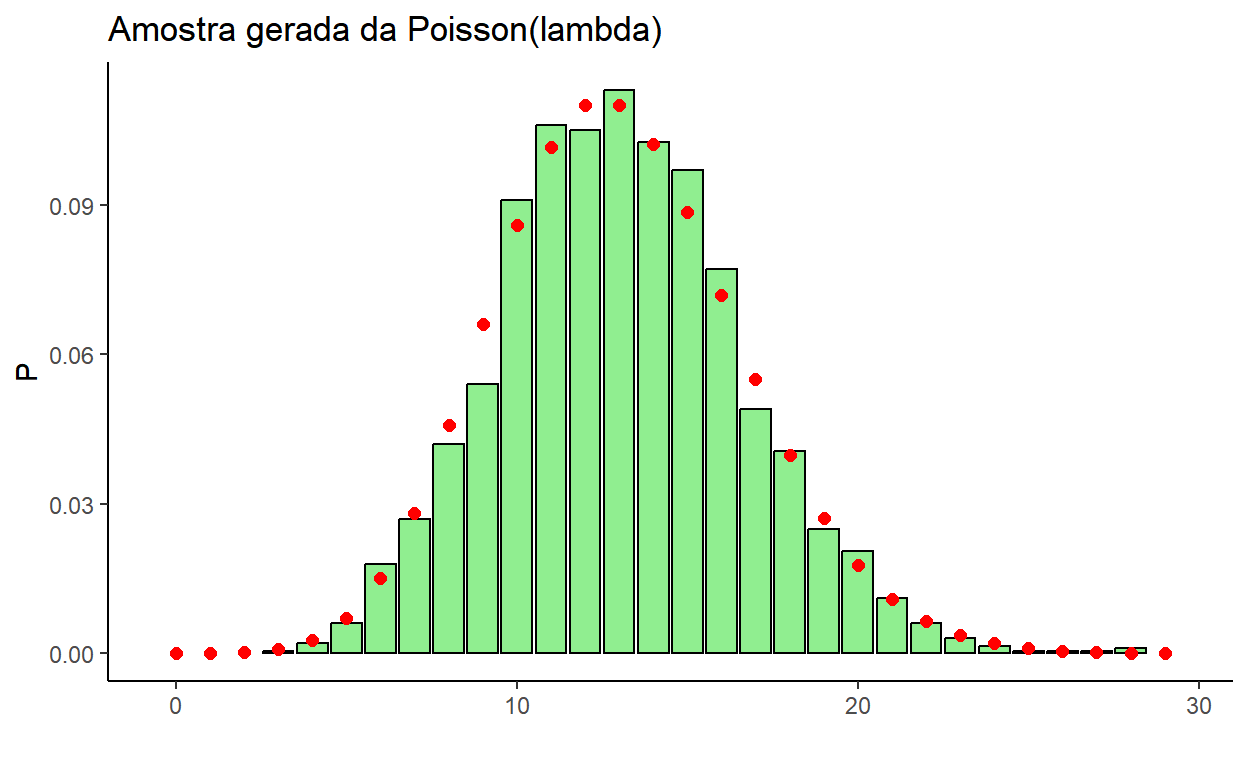
Como visto no curso de probabilidade, a função geradora de momentos da \(Poisson(\lambda)\) é \(M_X(t) = E[e^{tX}] = e^{\lambda(e^t-1)}\).
Para cada \(t\in\mathbb{R}\) fixado, podemos aproximar \(M_X(t)\) por \(\displaystyle \dfrac{1}{m}\sum_{i=1}^{m} e^{tx_i}\).
set.seed(666)
m=50; lambda=3
x <- rpois(m,lambda)
t <- seq(-0.1,0.1,0.001)
estimada <- apply(matrix(t),1,function(s){mean(exp(s*x))})
FGM <- tibble(t,estimada) %>%
mutate(fgm=exp(lambda*(exp(t)-1)))
FGM %>% ggplot() + theme_classic() + xlab("t") + ylab("M(t)") +
geom_line(aes(x=t, y=estimada), color="black", size=2) +
geom_line(aes(x=t, y=fgm), color="red", size=2,lty=3)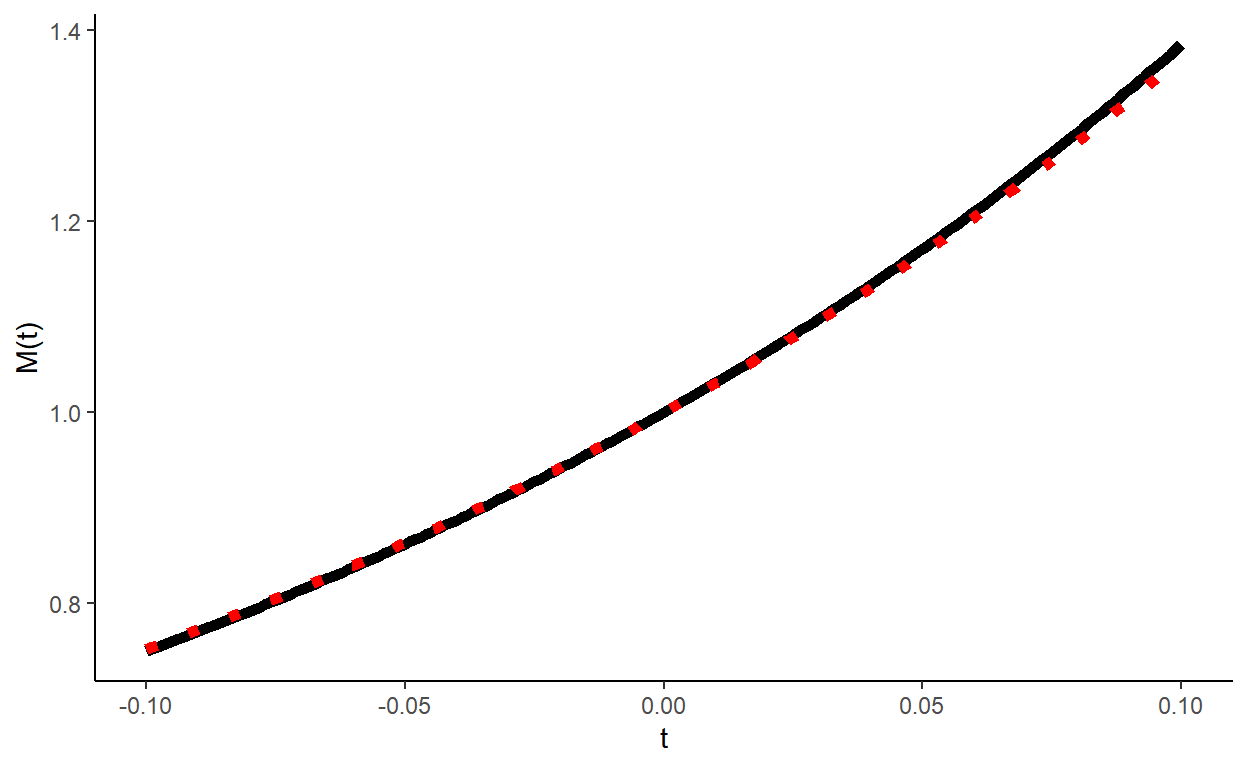
Teorema Central do Limite (TCL)
Seja \(X_1, X_2, \ldots\) uma sequência de variáveis aleatórias independentes e identicamente distribuídas (i.i.d.), com \(E[X_1]=\mu\) e \(Var(X_1)=\sigma^2<+\infty\). Considere \(\bar{X}_m = \frac{1}{m}\sum_{i=1}^mX_i\). Então, \[\frac{\bar{X}_m-\mu}{\sigma/\sqrt{m}} ~~\xrightarrow[m\rightarrow\infty]{\mathcal{D}}~~ Normal(0,1)~.\]
Quando \(m\) é “grande”, pode-se dizer que \(\bar{X}_m\) tem distribuição aproximadamente \(Normal\left(\mu,\frac{\sigma^2}{m}\right)\).
Para visualizar este resultado, rode os códigos abaixo mudando o tamanho amostral.
\(X_i \sim Bin(n,p)\)
set.seed(666)
m=2; p=0.6; n=10
M=1000
S=matrix(rbinom(m*M,n,p),ncol=M)
medias = colMeans(S)
hist(medias,probability = TRUE)
y=seq(4,10,0.001)
lines(y,dnorm(y,6,sqrt(2.4/m)),col="red")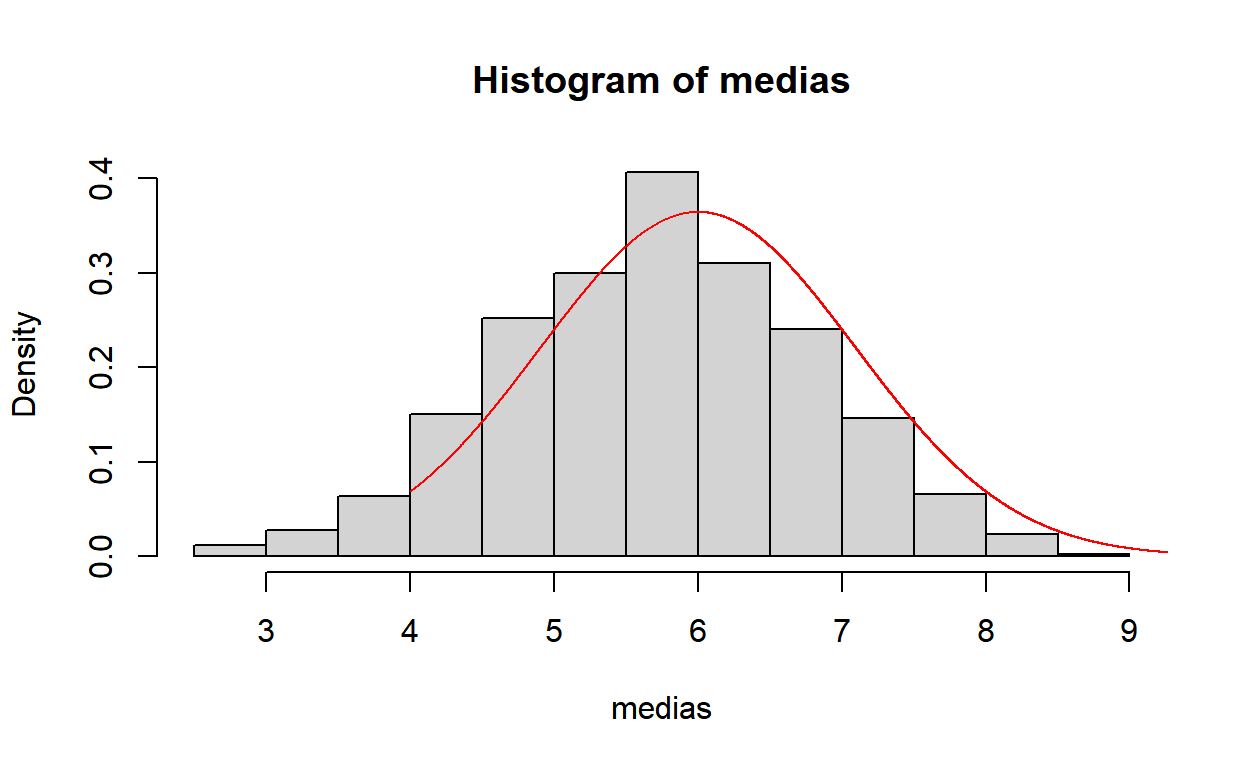
\(X_i \sim Poisson(\lambda)\)
set.seed(666)
m=2; lambda=13
M=1000
S=matrix(rpois(m*M,lambda),ncol=M)
medias = colMeans(S)
hist(medias,probability = TRUE)
y=seq(5,25,0.001)
lines(y,dnorm(y,lambda,sqrt(lambda/m)),col="red")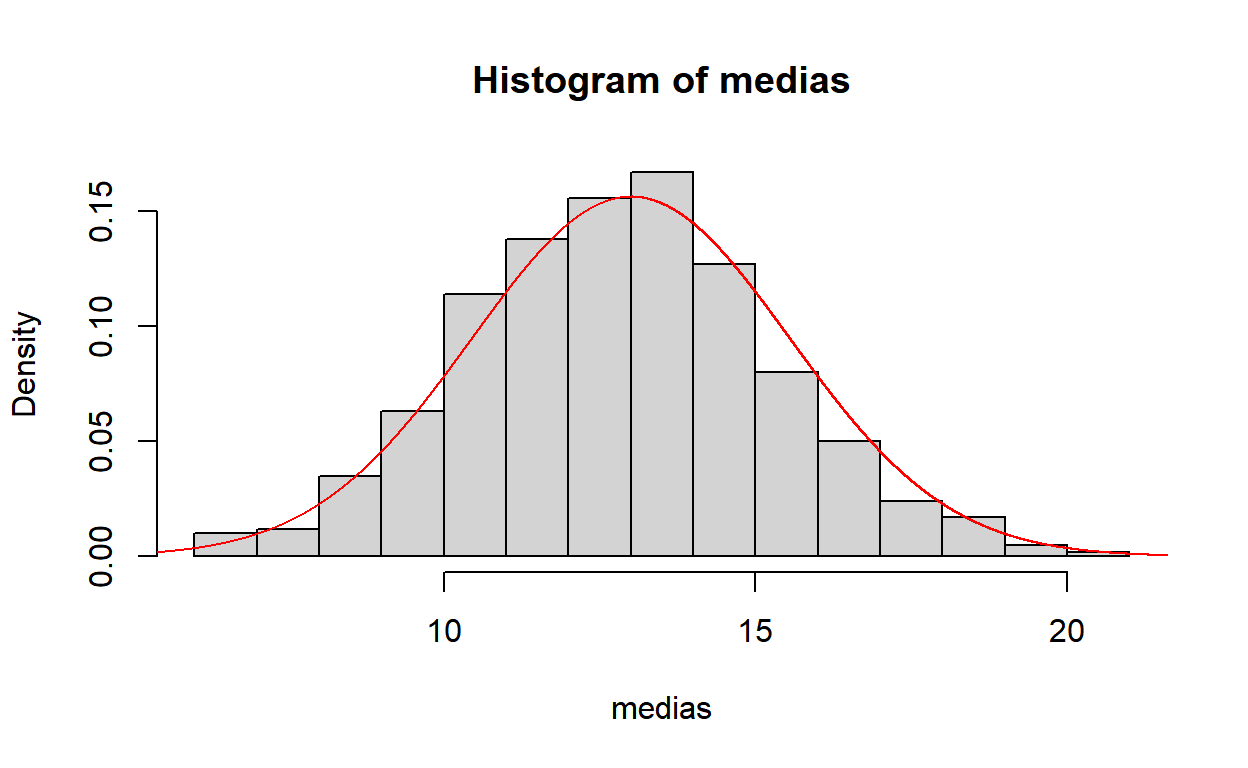
\(X_i \sim Geo(p)\)
Na parametrização do R, o \(X\) da distribuição geométrica representa o número de fracassos até o primeiro sucesso. Assim: \(P(X=x)= p(1-p)^{x}\), \(E[X] = \dfrac{1-p}{p}\) e \(Var(X)=\dfrac{1-p}{p^2}\).
Se você não sabe calcular \(E[X]\) e \(Var(X)\), pode aproximar esses valores pelos obtidos na amostra gerada.
m=2
M=1000
p=0.2
S=matrix(rgeom(m*M,p),ncol=M)
medias = colMeans(S)
hist(medias,probability = TRUE)
y=seq(0,25,0.001)
lines(y,dnorm(y,mean(medias),sqrt(var(medias))),col="red")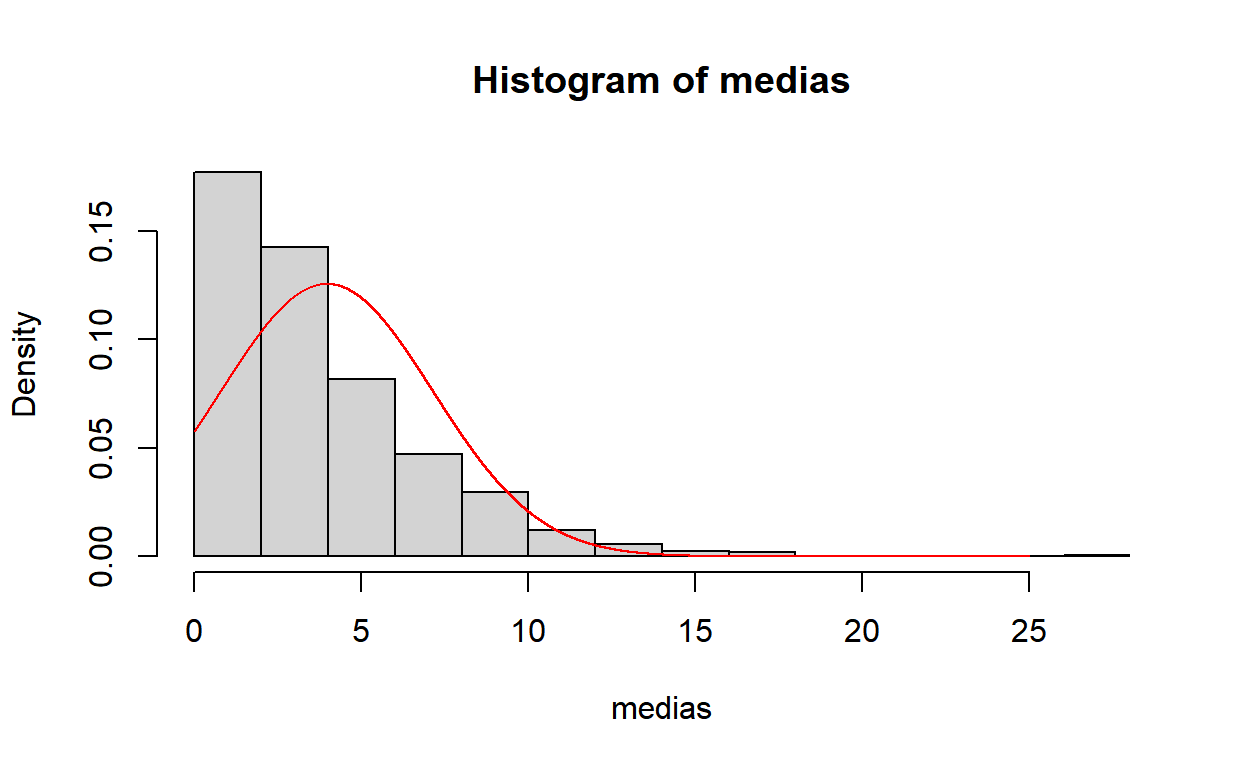
- Note que na Geométrica a aproximação para a Normal não é tão rápida quando nas distribuições anteriores. Em outras distribuições, a convergência pode demorar ainda mais.
Exemplos de Distribuições no R
O R tem diversas distribuições implementadas (e bibliotecas com muitas outras mais). As principais podem ser vistas com o comando
?Distributions.Considere a variável aleatória \(X\) com uma distribuição de probabilidade qualquer, chamada aqui genéricamente de
dist, com parâmetros que serão denotados porparam. Por exemplo, se \(X\sim \text{Binomial}(n,p)\), teremos no Rdist=binome os parâmetros serãosize(o número de experimentos de Bernoulli independentes, \(n\)) eprob(a probabilidade de sucesso, \(p\)).As funções disponíveis para a maioria das distribuições são
ddist(x,param): função de probabilidade \(P(X=x)\) no caso discreto ou função de densidade de probabilidade \(f(x)\) no caso contínuo.
pdist(q,param): função de distribuição (acumulada) \(F(x) = P(X\leq q)\).
rdist(n,param): função que gera \(n\) realizações i.i.d. (amostras) da variável aleatória \(X\) com distribuiçãodist.
qdist(p,param): função quantílica da distribuiçãodist, isto é, dada uma probabilidade \(p\), devolve o valor \(q\) tal que \(P(X\leq q)=p\). É o inverso da função de distribuição.
\(Binomial(n,p)\)
n=10; p=0.6
# P(X=x)
dbinom(2,n,p)[1] 0.01061683# Função de Probabilidade
tibble(x=seq(0,10)) %>% mutate(prob=dbinom(x,n,p)) %>%
ggplot() +
geom_point(aes(x=x,y=prob), color = "darkred", size = 3)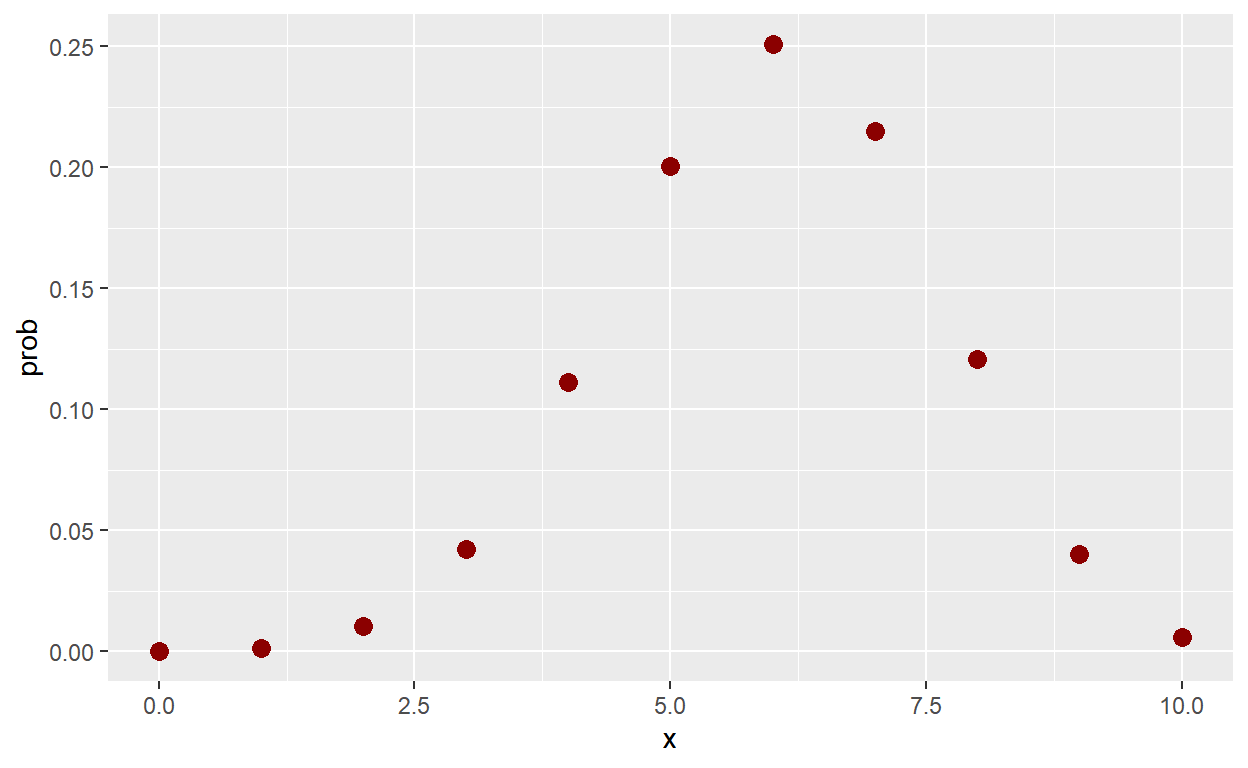
# P(X<=x)
pbinom(2,n,p)[1] 0.01229455[1] 0.01229455# Função de Distribuição
tibble(x=seq(0,10)) %>% mutate(prob=pbinom(x,n,p)) %>%
ggplot() +
geom_step(aes(x=x,y=prob), color = "darkred", size = 2)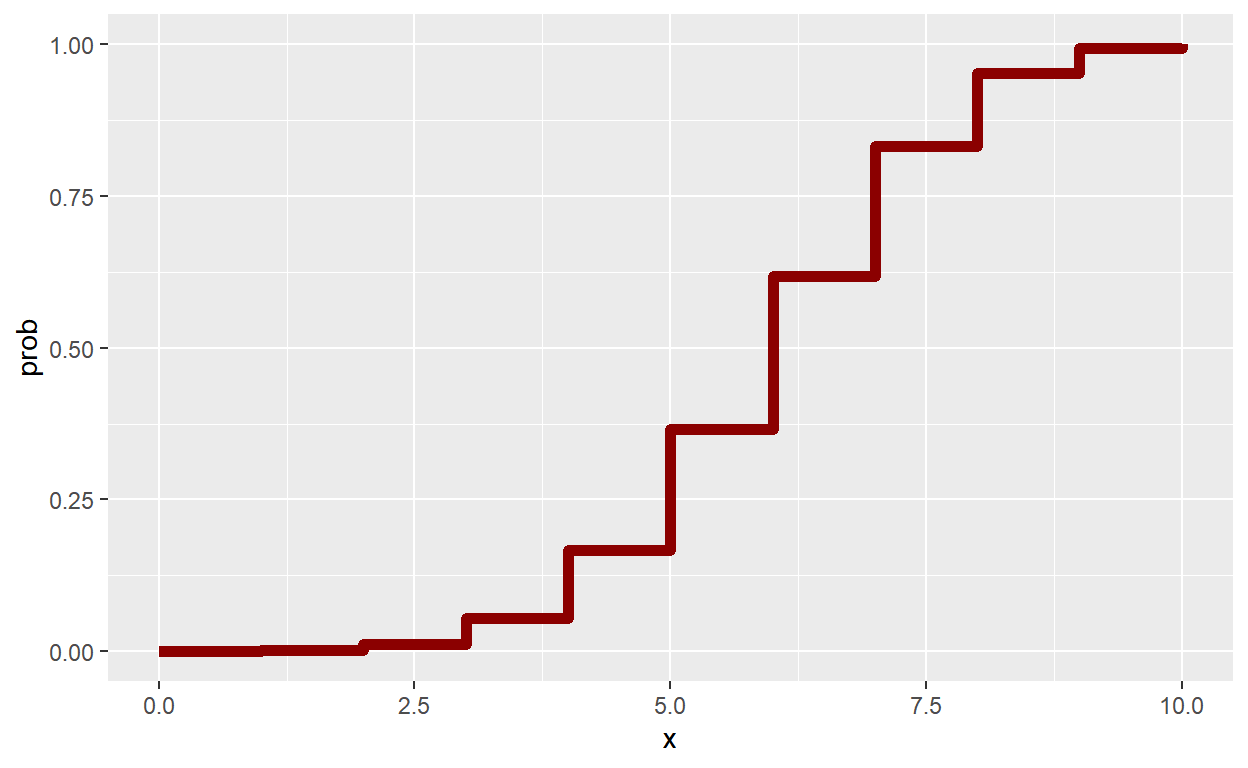
\(Poisson(\lambda)\)
lambda=3
# P(X=x)
dpois(2,lambda)[1] 0.2240418# Função de Probabilidade
tibble(x=seq(0,12)) %>% mutate(prob=dpois(x,lambda)) %>%
ggplot() +
geom_point(aes(x=x,y=prob), color = "darkred", size = 3)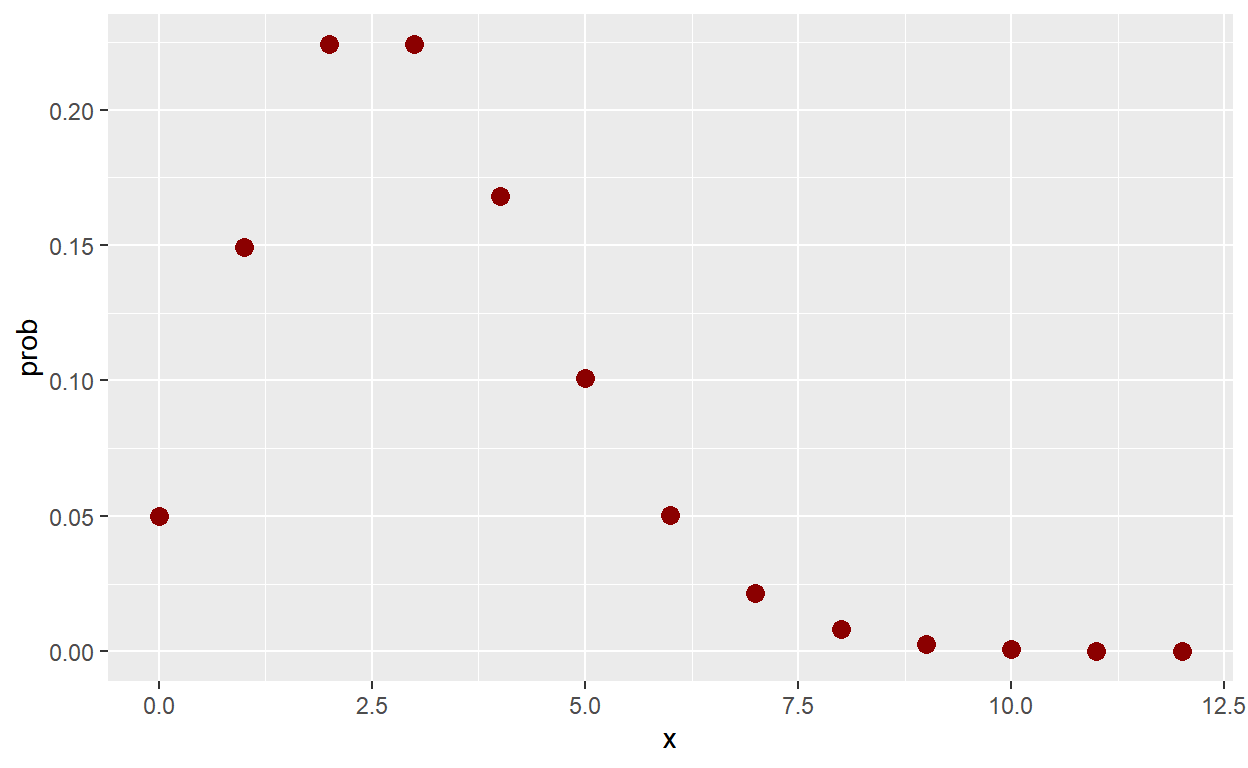
# P(X<=x)
ppois(2,lambda)[1] 0.4231901[1] 0.4231901# Função de Distribuição
tibble(x=seq(0,12)) %>% mutate(prob=ppois(x,lambda)) %>%
ggplot() +
geom_step(aes(x=x,y=prob), color = "darkred", size = 2)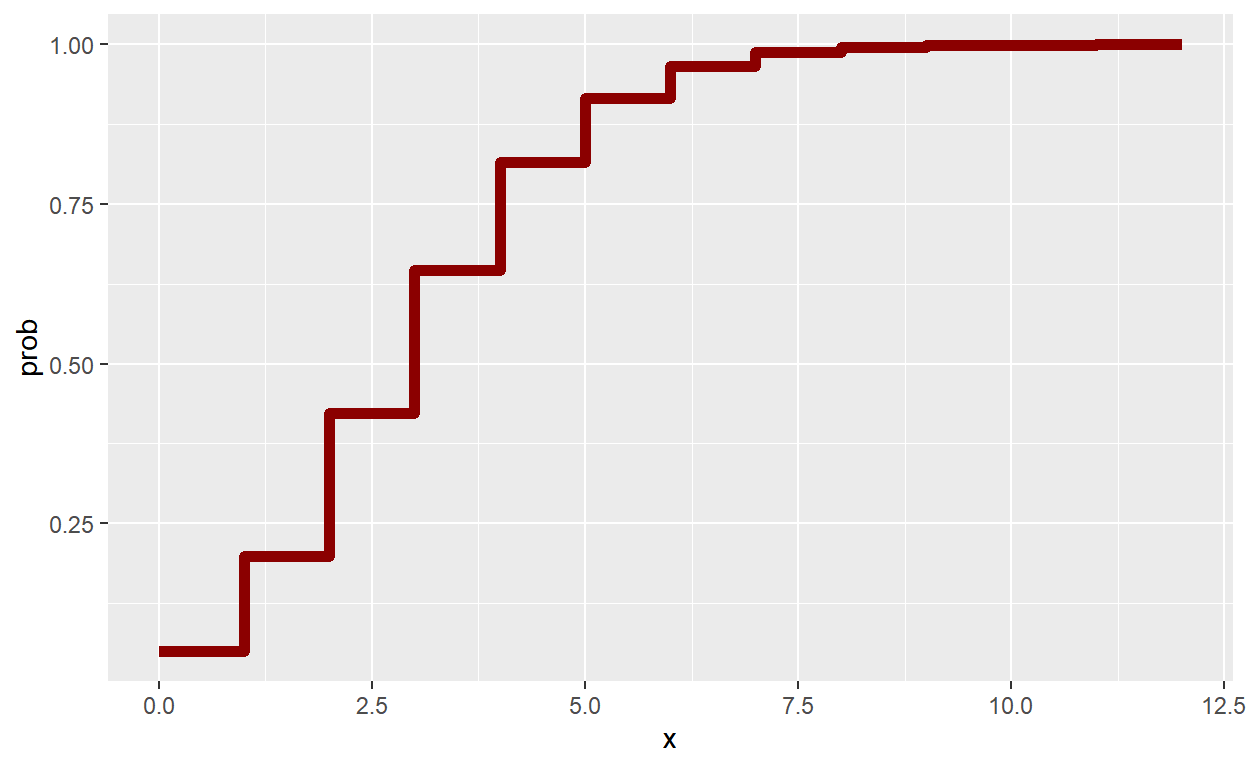
Distribuições Contínuas
\(Uniforme(0,1)\)
\(Normal(\mu,\sigma^2)\)
Distribuições de Outras Estatísticas
- Vamos novamente considerar uma amostra de tamanho \(m\) de \(X \sim Binomial(n,p)\), com \(n=10\) e \(p=0.6\).
Mínimo e Máximo
set.seed(666)
m=10; p=0.6; n=10
M=1000
S=matrix(rbinom(m*M,n,p),ncol=M)
minimos = apply(S,2,min)
bar1 <- ggplotify::as.ggplot(~barplot(table(minimos),
col="lightgreen", main="Mínimo"))
maximos = apply(S,2,max)
bar2 <- ggplotify::as.ggplot(~barplot(table(maximos),
col="lightgreen", main="Máximo"))
ggpubr::ggarrange(bar1,bar2)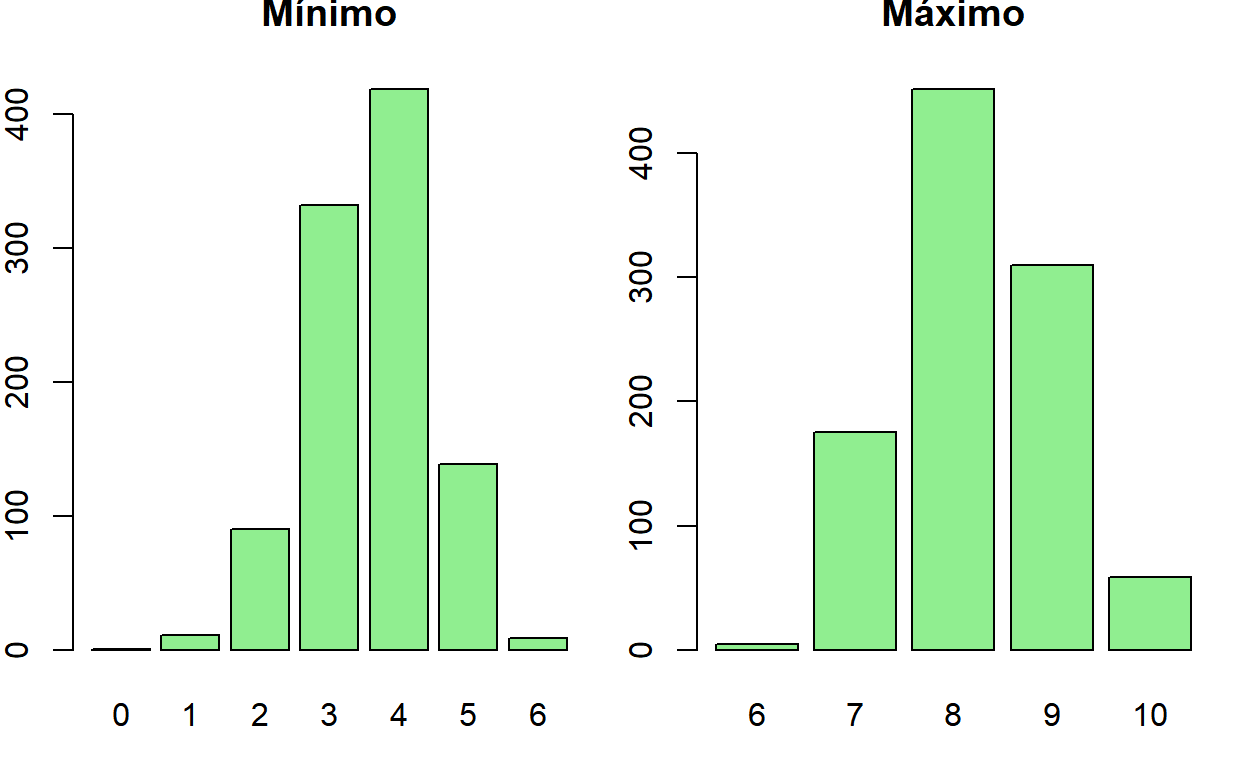
Variância e Desvio Padrão
set.seed(666)
m=10; p=0.6; n=10
M=1000
S=matrix(rbinom(m*M,n,p),ncol=M)
variancias = apply(S,2,var)
hist1 <- ggplotify::as.ggplot(~hist(variancias,
probability = TRUE,main="Variância",col="darkturquoise"))
dp=sqrt(variancias)
hist2 <- ggplotify::as.ggplot(~hist(dp,
probability = TRUE,main="Desvio Padrão",col="darkturquoise"))
ggpubr::ggarrange(hist1,hist2)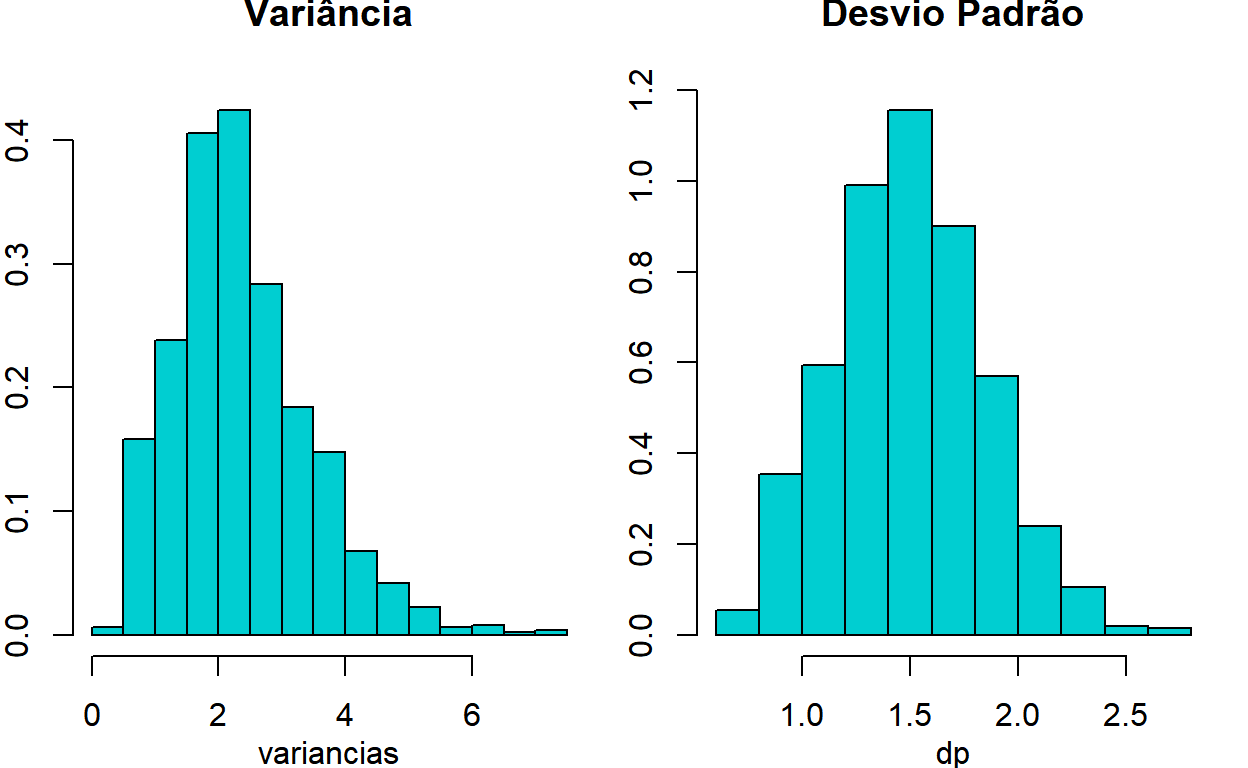
- Quando o tamanho amostral é suficientemente grande, podemos aplicar o TCL. No exemplo da variância, note que \(\displaystyle \frac{1}{m}\sum_{i=1}^{m} (X_i-\bar{X})^2\) é uma média e, pelo TCL, tem distribuição assintoticamente Normal.
set.seed(666)
m=100; p=0.6; n=10
M=1000
S=matrix(rbinom(m*M,n,p),ncol=M)
variancias = apply(S,2,var)
hist1 <- tibble(variancias) %>% ggplot() + theme_bw() +
ggtitle("Variância") +
geom_histogram(aes(x=variancias,y=..density..),
bins=nclass.Sturges(variancias),col="black",fill="darkturquoise") +
stat_function(fun=dnorm,
args=list(mean=mean(variancias),sd=sd(variancias)),
color="red",size=1)
dp=sqrt(variancias)
hist2 <- tibble(dp) %>% ggplot() + theme_bw() +
ggtitle("Desvio Padrão") +
geom_histogram(aes(x=dp,y=..density..),
bins=nclass.Sturges(variancias),col="black",fill="darkturquoise") +
stat_function(fun=dnorm,
args=list(mean=mean(dp),sd=sd(dp)),
color="red",size=1)
ggpubr::ggarrange(hist1,hist2)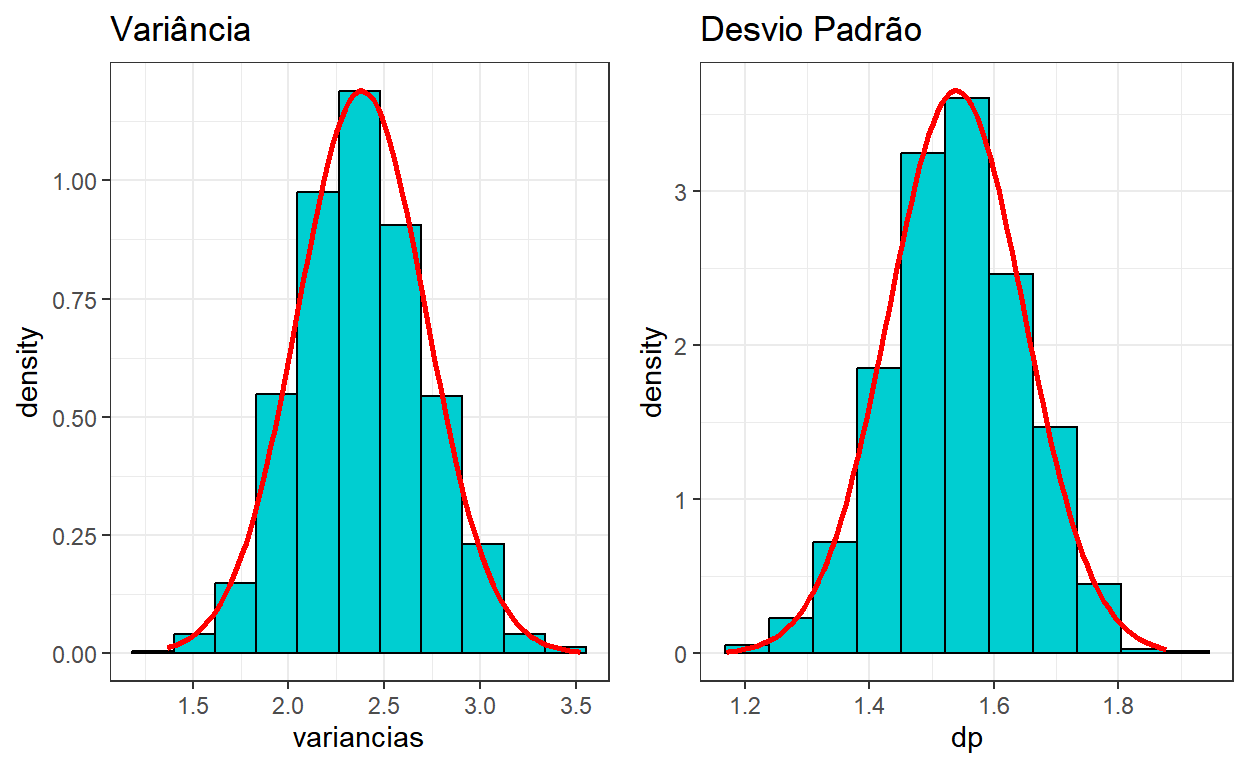
Reamostragem
Consiste em realizar \(M\) amostras de tamanho \(m\) com reposição da amostra original.
Usado para estimar a distribuição amostral de estatísticas de interesse. É possível mostrar que a distribuição obtida pelo método converge para a teórica conforme o tamanho amostral aumenta.
Para detalhes, ver, por exemplo, o livro B. Efron, R. Tibshirani. (1993). An Introduction to the Bootstrap. Chapman & Hall/CRC. ISBN 0-412-04231-2.
set.seed(666)
m=200; p=0.6; n=10
M=1000
S=matrix(rbinom(m*M,n,p),ncol=M)
variancias = apply(S,2,var)
b=c(min(variancias),max(variancias),nclass.Sturges(variancias))
hist1 <- tibble(variancias) %>% ggplot() + theme_bw() +
ggtitle("Várias Amostras") + xlim(b[1],b[2]) +
geom_histogram(aes(x=variancias,y=..density..),
bins=b[3],col="black",fill="lightgreen")
# Realiza amostras de tamanho n com reposição da primeira amostra gerada
B <- apply(matrix(rep(1,M)),1,
function(y){sample(S[,1],length(S[,1]),replace=TRUE)})
variancias = apply(B,2,var)
hist2 <- tibble(variancias) %>% ggplot() + theme_bw() +
ggtitle("Reamostragem") + xlim(b[1],b[2]) +
geom_histogram(aes(x=variancias,y=..density..),
bins=b[3],col="black",fill="darkturquoise")
ggpubr::ggarrange(hist1,hist2,ncol=1)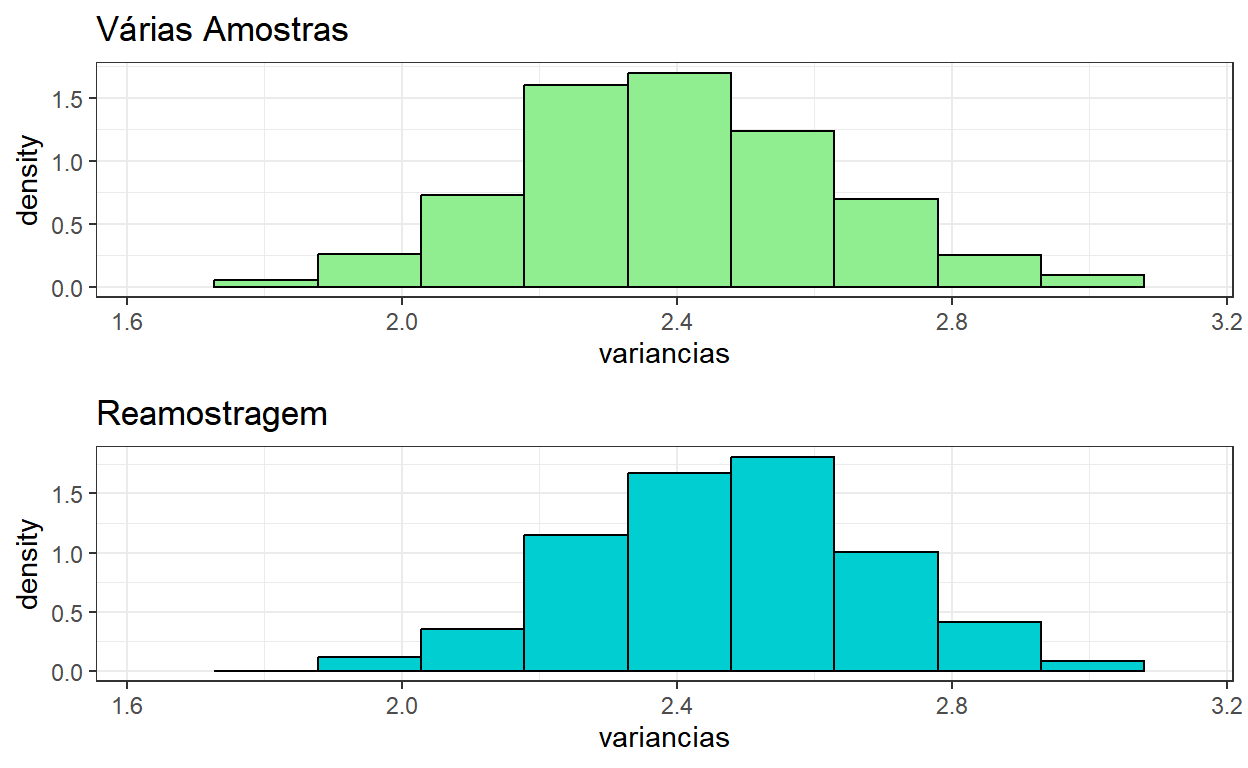
Aplicação do TCL
- Seja \(X_1, X_2, \ldots,X_n\) uma sequência de variáveis aleatórias (v.a.) independentes e identicamente distribuídas (i.i.d.). Quando o tamanho amostral \(n\) é “grande”, vimos pela LGN que \(\bar{X}=\dfrac{1}{n}\sum X_i\longrightarrow E[X_1]\), \(\dfrac{1}{n}\sum (X_i-\bar{X})^2\longrightarrow Var(X_1)\) e, pelo TCL, que \(\bar{X}_n \approx \text{Normal}\left(E[X_1]~,~\dfrac{Var(X_1)}{n}\right)\).
Exemplo: Seja \(X_1, X_2, \ldots,X_{n}\) v.a. i.i.d. tais que \(X_1\sim \text{Ber}(p)\). Suponha \(n=100\), \(p=0.6\) e que você deseja calcular \(\displaystyle P\left(\sum_{i=1}^{100}X_i <= 50\right)\). Então,
\[P\left(\sum_{i=1}^{100}X_i \leq 58\right) = P\left(\frac{\sum_{i=1}^{100}X_i}{100} \leq \frac{58}{100}\right)\approx P\left(Y \leq 0.58\right)~,\] em que \(Y\sim \text{Normal}\left(p,\dfrac{p(1-p)}{n}\right)\).
- Usando o R:
- Note que \(\displaystyle \sum_{i=1}^{100}X_i \sim \text{Binomial}\left(n=100,p=0.6\right)\), de modo que a probabilidade desejada pode ser calculada de forma exata como:
pbinom(58,100,0.6)[1] 0.3774673- Visualmente, temos:
n=100; p=0.6
# Função de Distribuição
tibble(x=seq(qbinom(0.01,n,p),qbinom(0.99,n,p),1)) %>% mutate(prob=pbinom(x,n,p)) %>%
ggplot() +
# Binomial
geom_step(aes(x=x,y=prob), color = "darkred", size = 2) +
# Normal
stat_function(fun=pnorm,
args=list(mean=n*p,sd=sqrt(n*p*(1-p))),
color="green",size=1)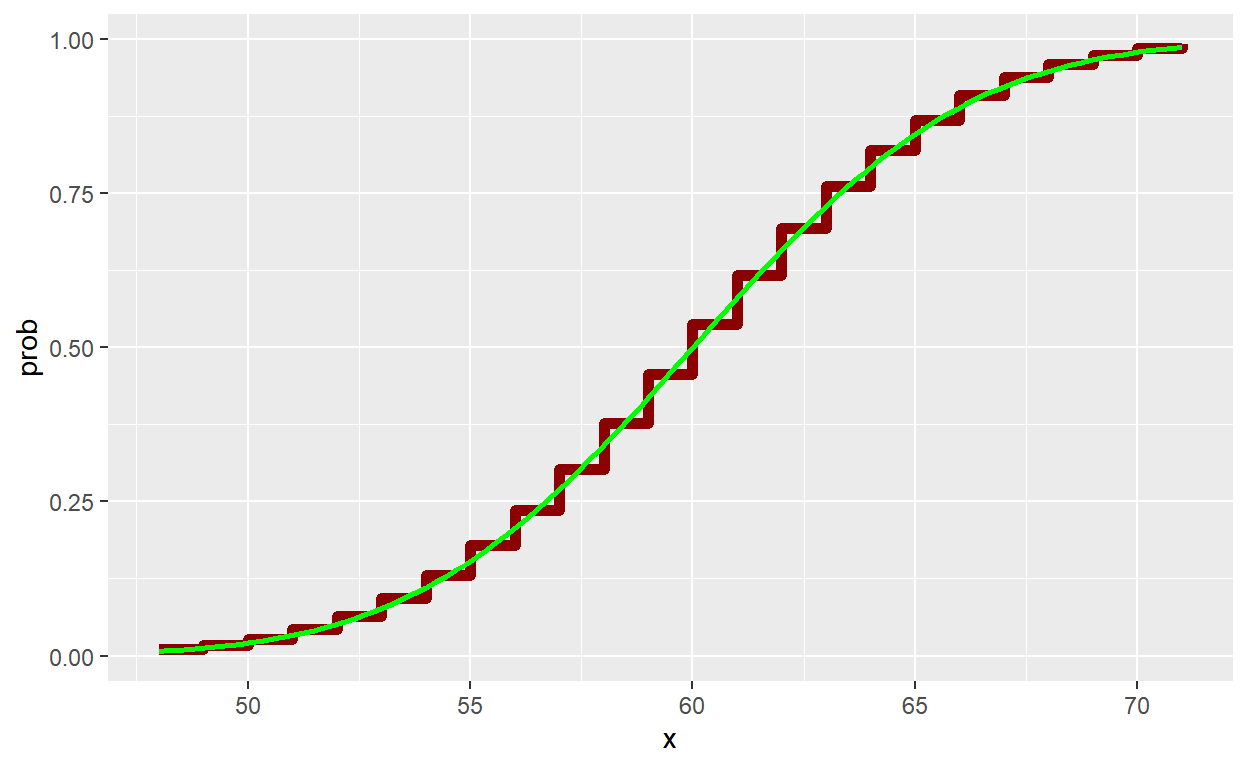
- O TCL garante convergência nos pontos de continuidade da \(F\). Assim, é comum usar uma “correção de continuidade”, fazendo \[P\left(\sum_{i=1}^{100}X_i \leq 58\right) = P\left(\sum_{i=1}^{100}X_i \leq 58+0.5\right)\approx P\left(Y \leq 0.585\right)~.\]
Função de Distribuição Empírica
Em aplicações de Estatística, em geral, não conhecemos a distribuição teórica.
Como já visto, podemos aproximar a função de probabilidade (no caso discreto) ou função de densidade de probabilidade (no caso contínuo), pelas frequências relativas ou histograma, respectivamente.
De forma análoga, podemos aproximar a função de distribuição \(F\) pela função de distribuição empírica \(F_n\), definida por: \[F_n(x) = \frac{1}{n} \sum_{i=1}^{n}\mathbb{I}(x_i\leq x)\]
Para cada \(t\in \mathbb{R}\), a LGN garante que \(F_n(t) ~\xrightarrow[n\rightarrow\infty]~F(t)\). O Teorema de Glivenko–Cantelli garante que \(F_n\) converge uniformemente para \(F\), isto é, \(\displaystyle \sup_{t \in \mathbb{R}}\left|F_n(t)-F(t)\right|~\xrightarrow[n\rightarrow\infty]~0\).
Exemplo 1: Amostra de tamanho \(m\) da \(\text{Binomial}(n,p)\)
m=100
n=10; p=0.6
set.seed(666)
s <- rbinom(m,n,p)
# Função de Probabilidade
teorica <- tibble(x=seq(0,n),Prob = dbinom(x,n,p))
amostra <- tibble(x=s) %>% group_by(x) %>%
summarise(FreqRel = n()) %>%
mutate(FreqRel = FreqRel/sum(FreqRel))
left_join(teorica,amostra,by="x") %>%
ggplot() + theme_classic() + xlab("") + ylab("P") +
ggtitle("Amostra gerada da Bin(n,p)") +
xlim(0-0.5,n+0.5) +
geom_col(aes(x=x, y=FreqRel),
color="black", fill="rosybrown2") +
geom_point(aes(x=x, y=Prob), color="darkgreen", size=3)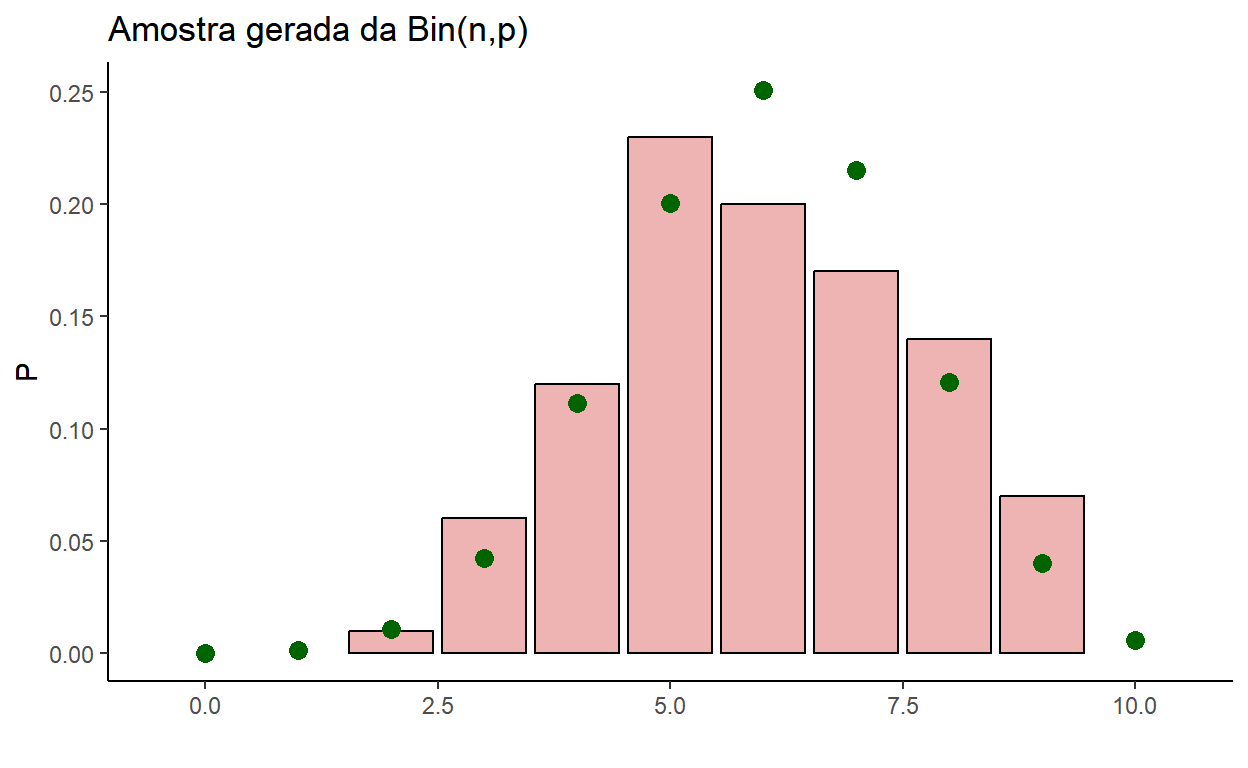
# Função de Distribuição
tibble(s) %>%
ggplot() + theme_bw() + xlim(-0.5,n+0.5) +
# Empirica
stat_ecdf(aes(x=s), color = "darkred", size = 2) +
# Teorica
stat_function(fun=pbinom, args=list(size=n,prob=p),
color="green",size=1,n=2000)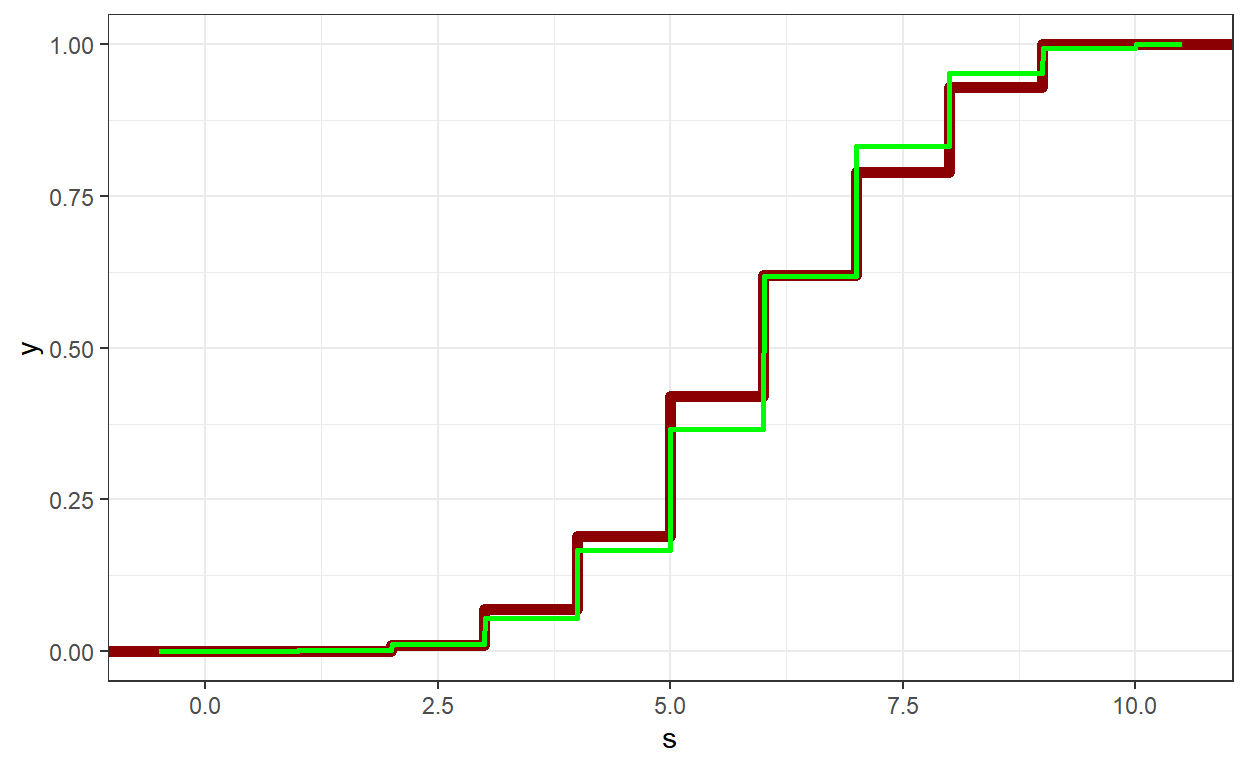
Exemplo 2: Amostra de tamanho \(m\) da \(\text{Normal}\left(\mu,\sigma^2\right)\)
m=100
mu=0; sigma=1
set.seed(666)
s <- rnorm(m,mu,sigma)
# Função de Densidade de Probabilidade
tibble(s) %>% ggplot() + theme_classic() + xlab("") + ylab("f") +
ggtitle("Amostra gerada da Normal(mu,sigma^2)") +
xlim(qnorm(0.001,mu,sigma),qnorm(0.999,mu,sigma)) +
geom_histogram(aes(x=s, y=..density..),
bins=nclass.Sturges(s),
color="black", fill="rosybrown2") +
stat_function(fun=dnorm, args=list(mean=mu,sd=sigma),
color="darkgreen",size=1,n=2000)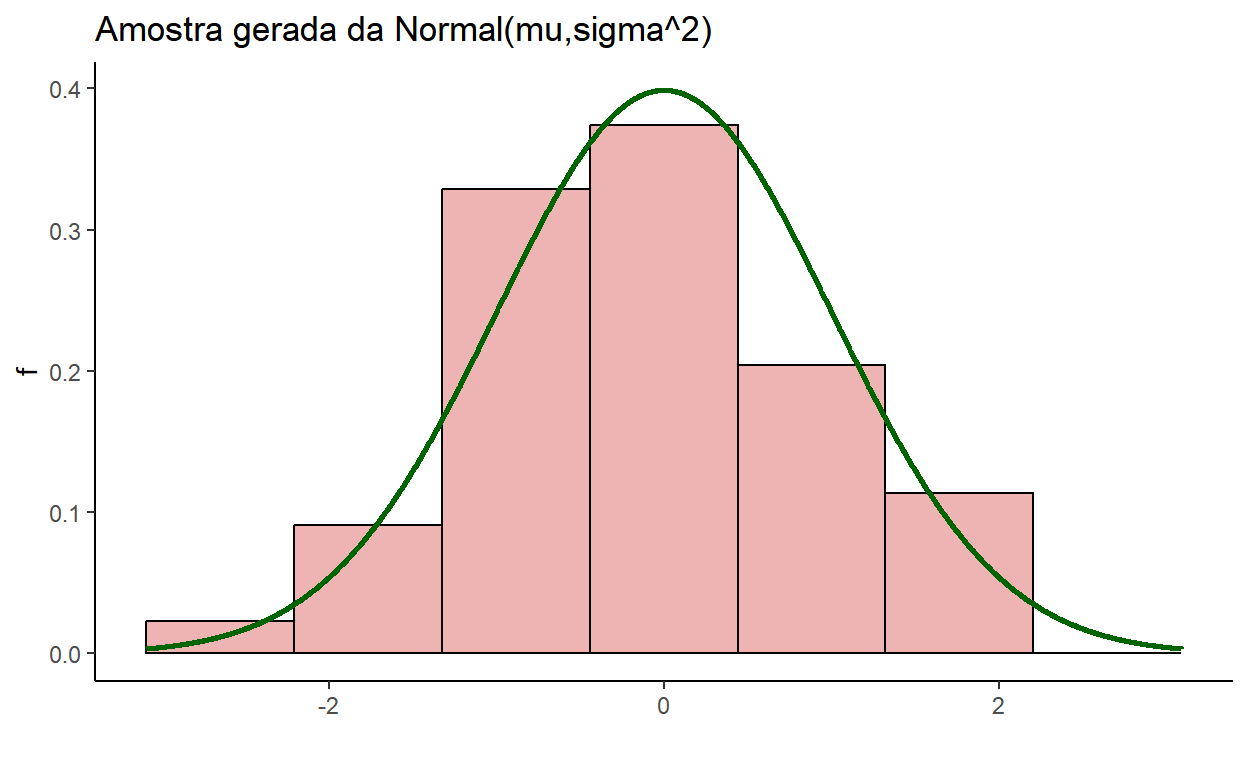
# Função de Distribuição
tibble(s) %>%
ggplot() + theme_bw() +
xlim(qnorm(0.005,mu,sigma),qnorm(0.995,mu,sigma)) +
# Empirica
stat_ecdf(aes(x=s), color = "darkred", size = 2) +
# Teorica
stat_function(fun=pnorm, args=list(mean=mu,sd=sigma),
color="green",size=1,n=2000)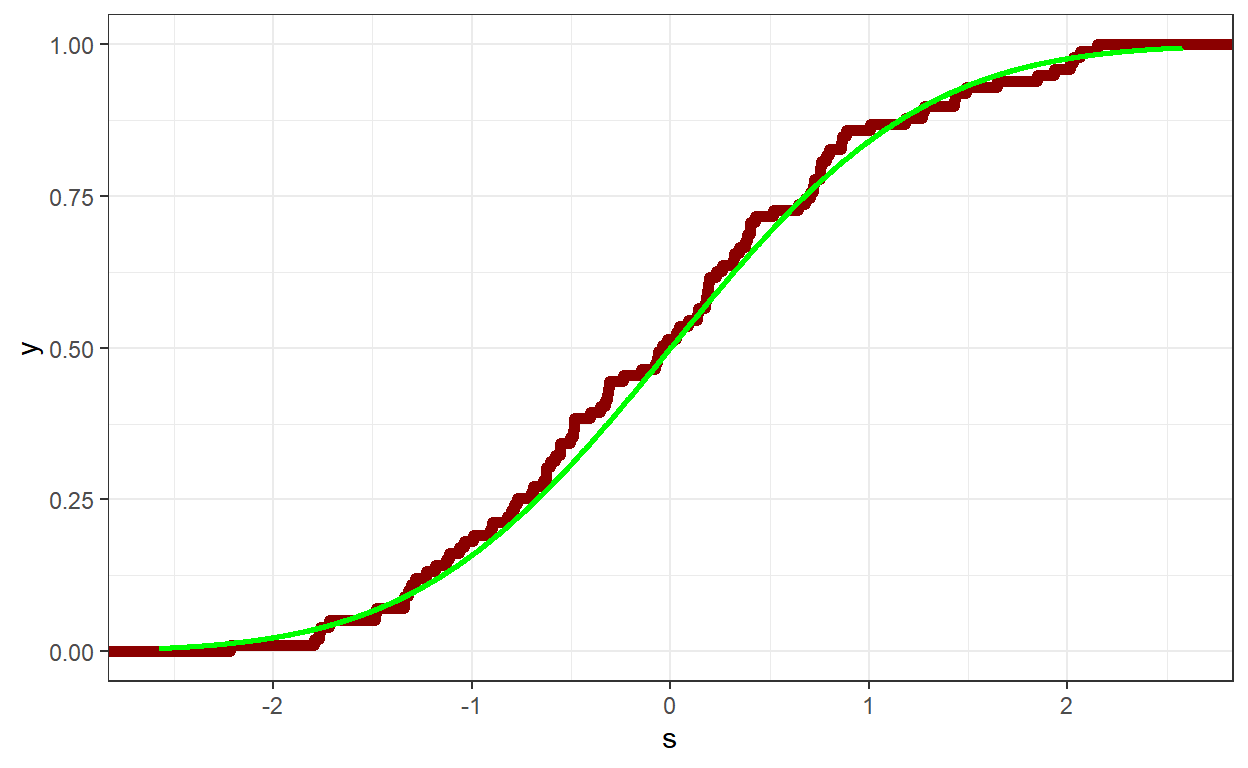
Exemplo da Aula Passada: Amostra de tamanho \(m\) da \(\text{Normal}\left(\mu,\sigma^2\right)\)
m=100
mu=0; sigma=1
set.seed(666)
s <- rnorm(m,mu,sigma)
# Função de Densidade de Probabilidade
tibble(s) %>% ggplot() + theme_classic() + xlab("") + ylab("f") +
ggtitle("Amostra gerada da Normal(mu,sigma^2)") +
xlim(qnorm(0.001,mu,sigma),qnorm(0.999,mu,sigma)) +
geom_histogram(aes(x=s, y=..density..),
bins=nclass.Sturges(s),
color="black", fill="rosybrown2") +
stat_function(fun=dnorm, args=list(mean=mu,sd=sigma),
color="darkgreen",size=1,n=2000)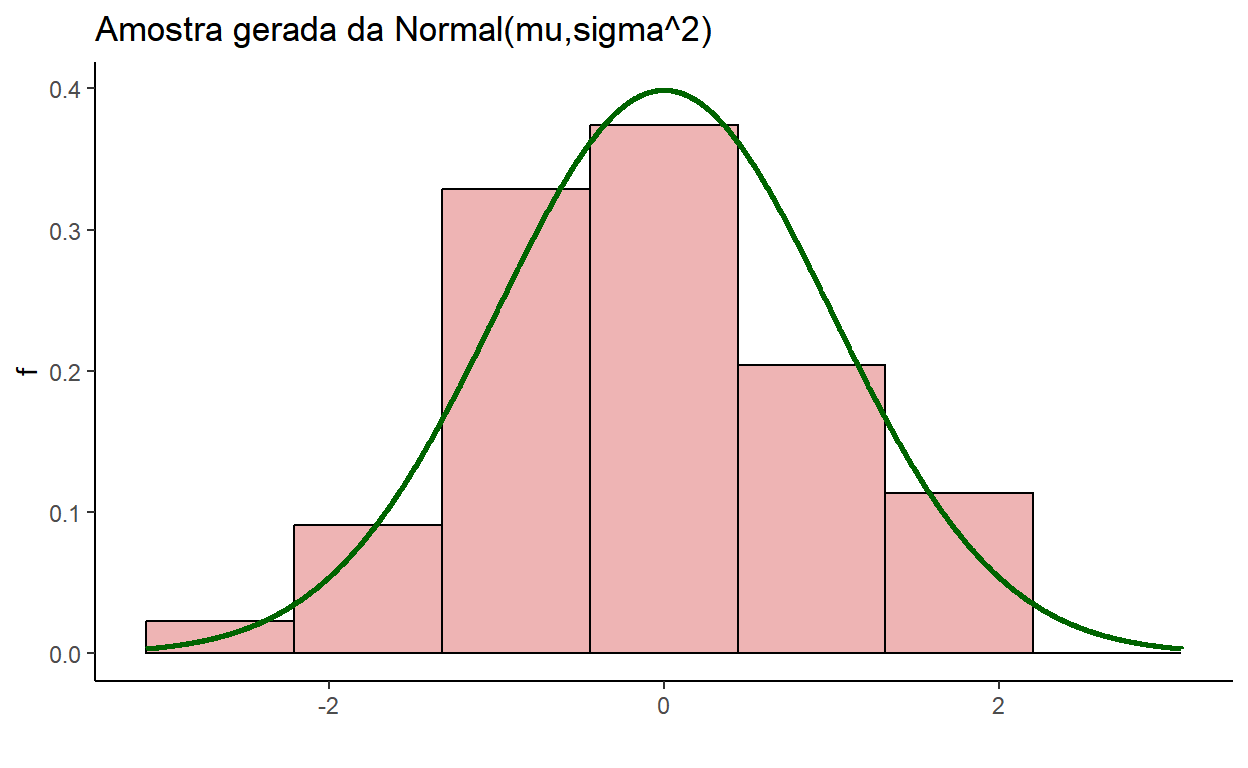
# Função de Distribuição
tibble(s) %>%
ggplot() + theme_bw() +
xlim(qnorm(0.005,mu,sigma),qnorm(0.995,mu,sigma)) +
# Empirica
stat_ecdf(aes(x=s), color = "darkred", size = 2) +
# Teorica
stat_function(fun=pnorm, args=list(mean=mu,sd=sigma),
color="green",size=1,n=2000)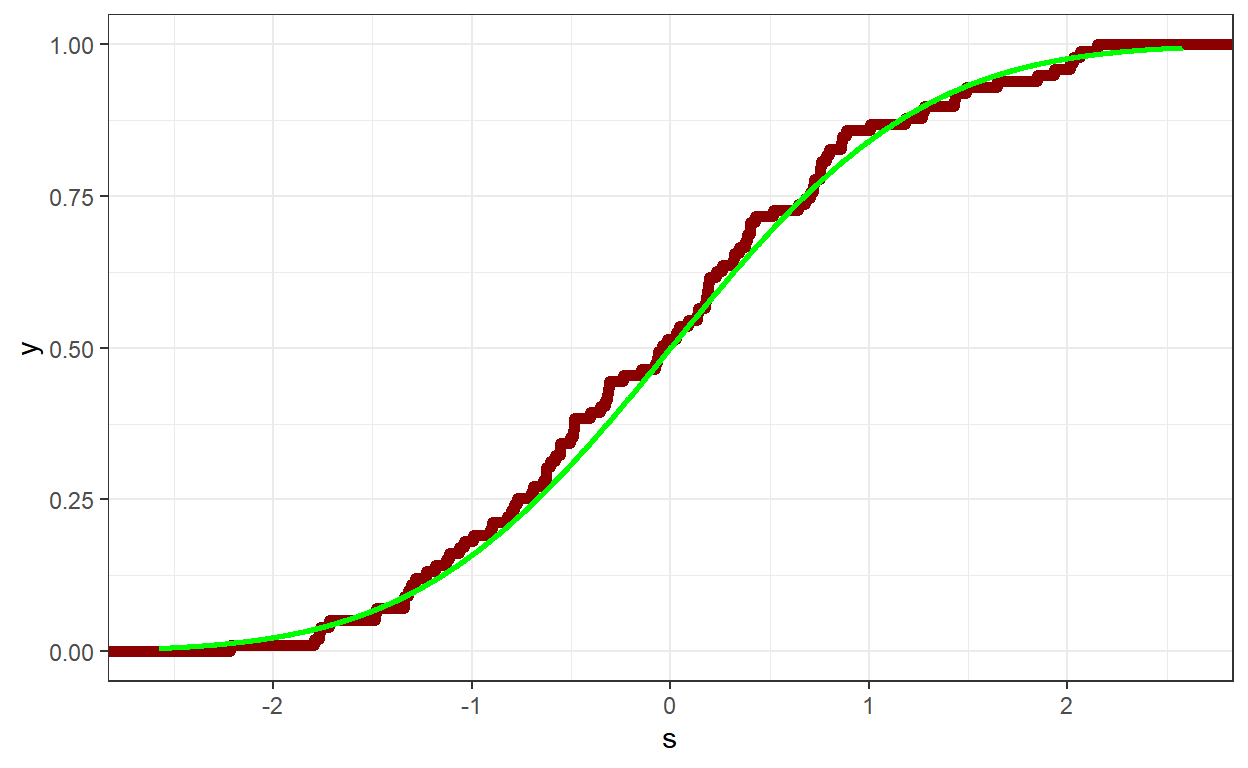
Estimativa da Densidade por Kernel (KDE)
Seja \(X_1,\ldots,X_n\) v.a. i.i.d. com distribuição que possui função de densidade de probabilidade desconhecida \(f\). A estimativa de densidade por Kernel é dada por: \[\hat{f}(x) = \frac{1}{nh}\sum_{i=1}^{n}K\left(\frac{x-x_i}{h}\right)~~,\] em que \(h\) é um parâmetro chamado largura da banda e \(K\) é um kernel, isto é, uma função integrável não-negativa. Normalmente, \(K\) é escolhido de modo que \(K(-u)=K(u)\), \(\forall u\), e \(\displaystyle \int_{-\infty}^{\infty} K(u)~du=1\). \(K\) pode ser, por exemplo, a densidade de uma normal com média igual a zero.
No exemplo anterior, teríamos:
m=100
mu=0; sigma=1
set.seed(666)
s <- rnorm(m,mu,sigma)
# Função de Densidade de Probabilidade
tibble(s) %>% ggplot() + theme_classic() + xlab("") + ylab("f") +
ggtitle("Amostra gerada da Normal(mu,sigma^2)") +
xlim(qnorm(0.0005,mu,sigma),qnorm(0.9995,mu,sigma)) +
geom_density(aes(x=s),#, y=..density..),
#bins=nclass.Sturges(s),
color="black", fill="rosybrown2") +
stat_function(fun=dnorm, args=list(mean=mu,sd=sigma),
color="darkgreen",size=1,n=2000)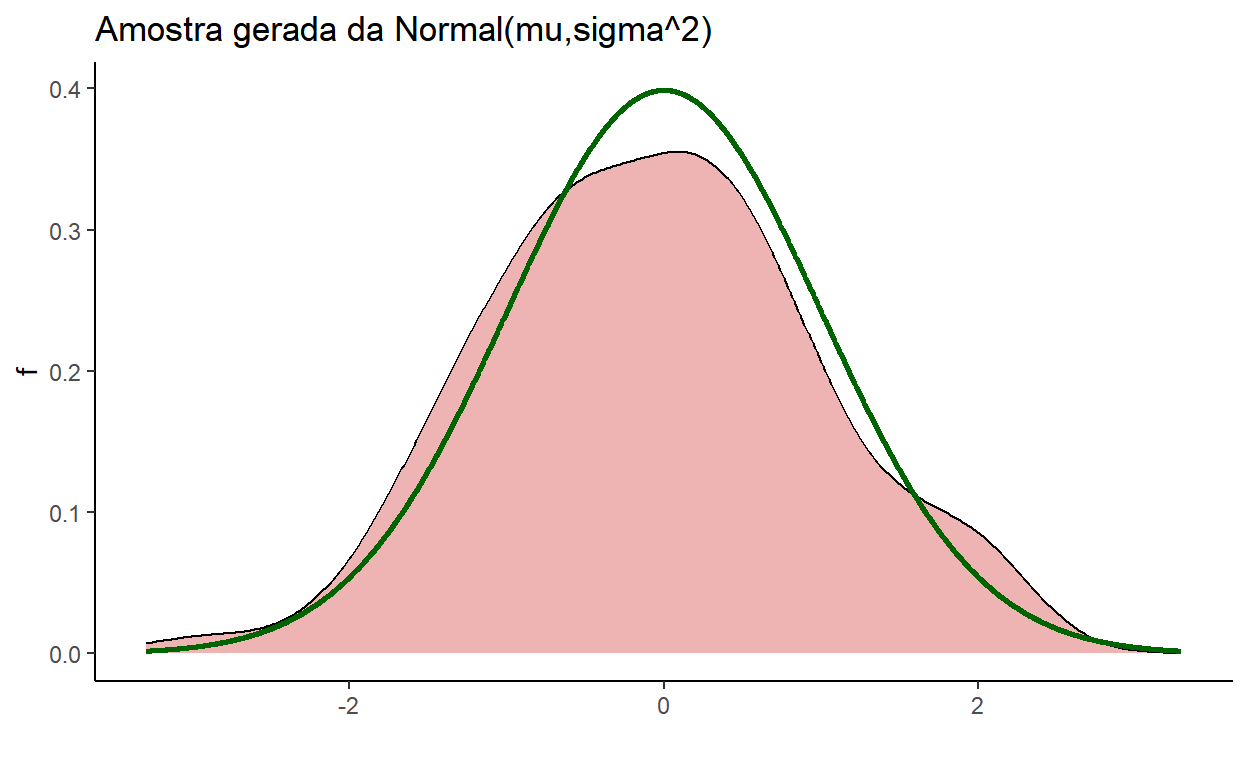
# Função de Distribuição
# KDE para F
e = 0.3*diff(range(s))
dens = density(s,from=min(s)-e,to=max(s)+e)
tibble(x=dens$x, y=dens$y) %>% mutate(y=cumsum(y)/sum(y)) %>%
ggplot() + theme_bw() +
xlim(qnorm(0.001,mu,sigma),qnorm(0.999,mu,sigma)) +
# Empirica
geom_line(aes(x=x, y=y), linewidth=2, colour='darkred') +
# Teorica
stat_function(fun=pnorm, args=list(mean=mu,sd=sigma),
color="green",size=1,n=2000)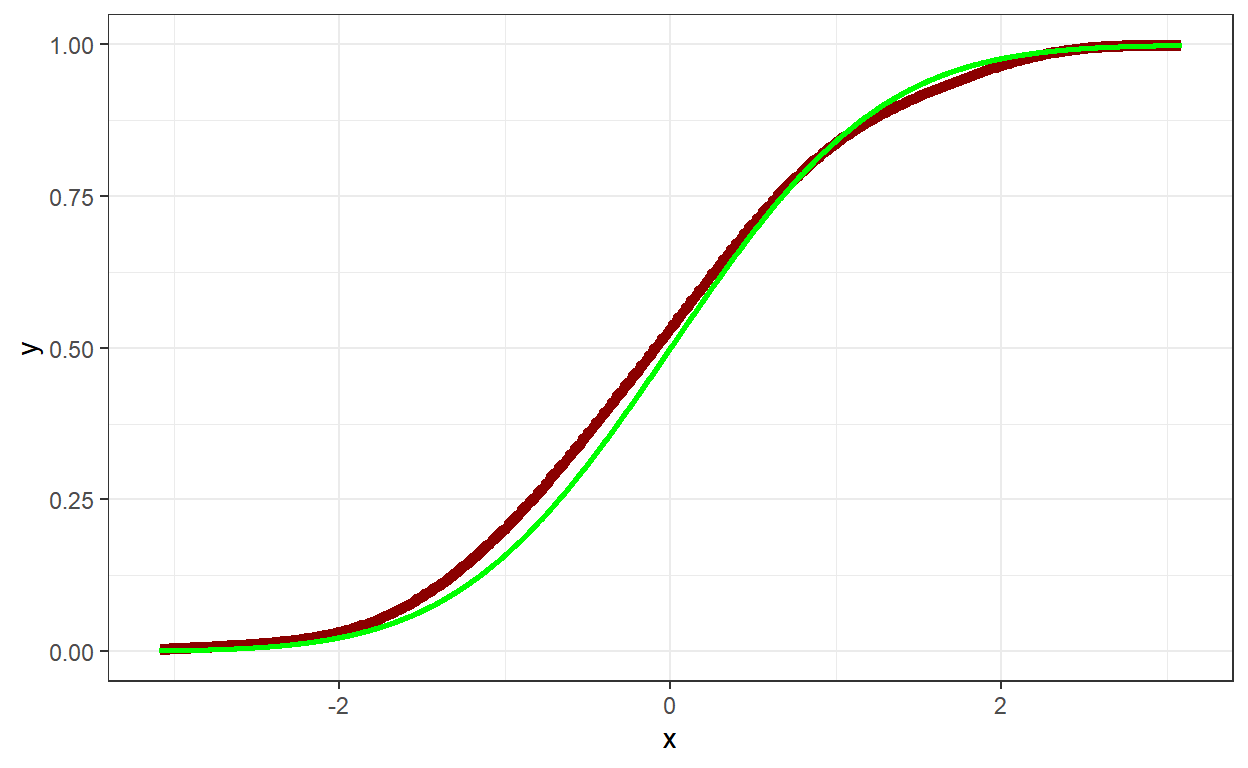
- No exemplo da Altura:
dados <- read_csv("dados\\exemplo_dados.csv")
dados %>% ggplot() + theme_bw() +
geom_histogram(aes(x=Altura,after_stat(density)),
breaks=c(seq(1.5,1.91,length.out=6)),
color="black", fill="darkgreen") +
geom_density(aes(x=Altura), color="black", fill="lightgreen",
alpha = 0.4, bounds=c(1.45,1.96))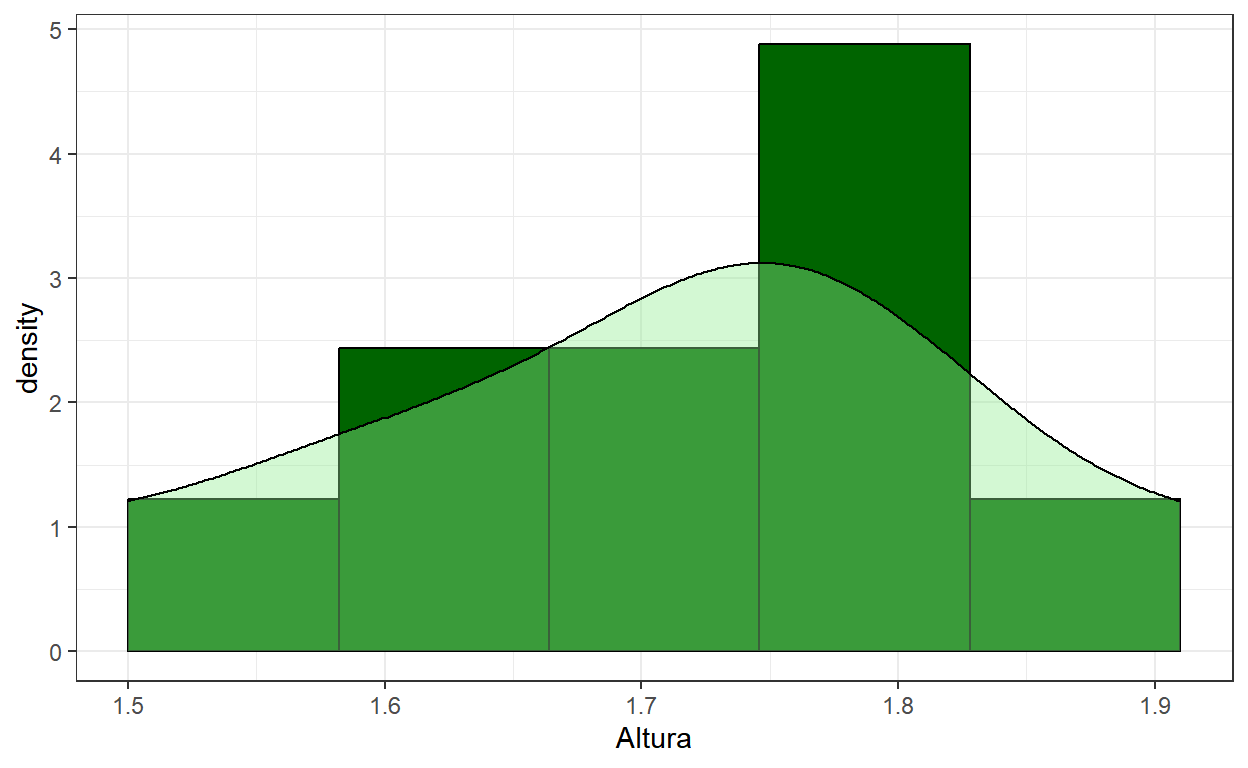
# Função de Distribuição
# KDE para F
e = 0.3*diff(range(dados$Altura))
dens = density(dados$Altura,from=min(dados$Altura)-e,to=max(dados$Altura)+e)
tibble(x=dens$x, y=dens$y) %>% mutate(y=cumsum(y)/sum(y)) %>%
ggplot() + theme_bw() +
# Empirica
stat_ecdf(data=dados, aes(x=Altura), color="darkred",size=2) +
# Empirica "alisada"
geom_line(aes(x=x, y=y), linewidth=1, colour='red')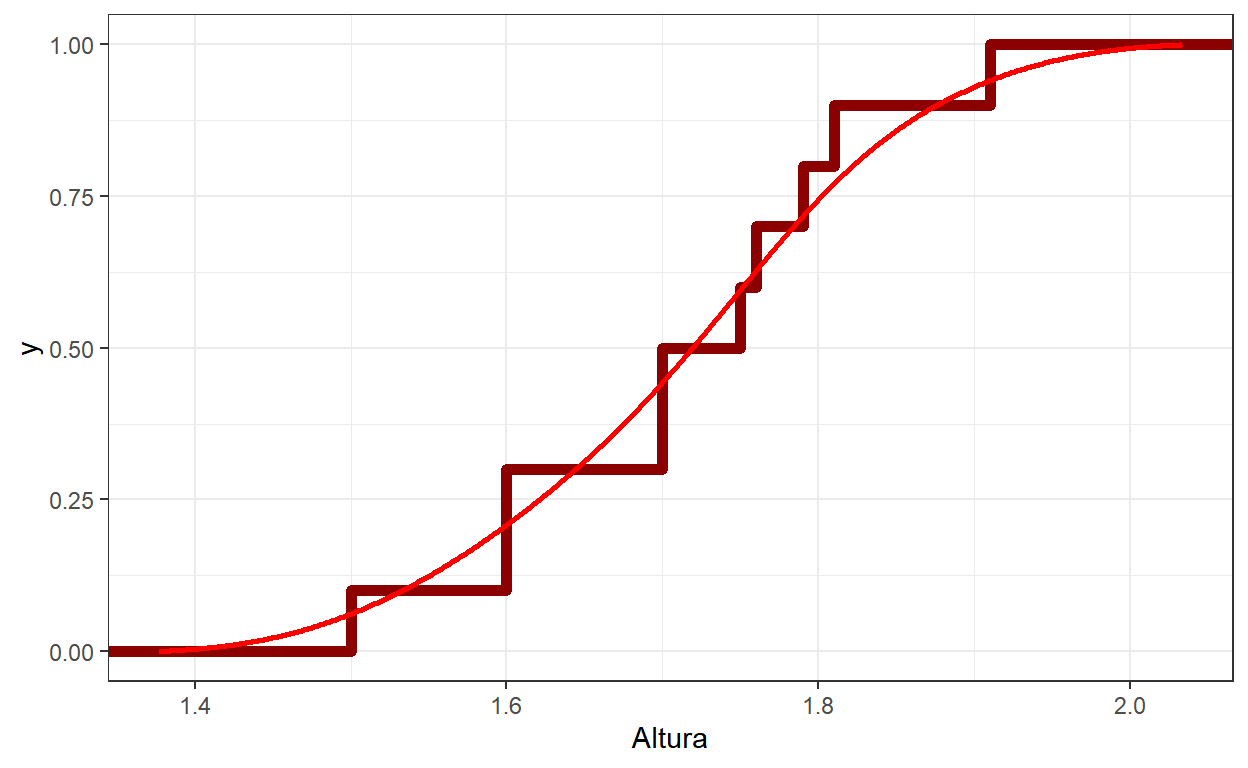
Comparação de distribuições
- Considere a variável Número de Livros dos dados usados nas primeiras aulas.
| Nlivros | FreqObs | FreqRel | Fn |
|---|---|---|---|
| 0 | 2 | 0.2 | 0.2 |
| 1 | 4 | 0.4 | 0.6 |
| 2 | 2 | 0.2 | 0.8 |
| 3 | 2 | 0.2 | 1.0 |
Uma pergunta que pode ser feita é se os dados observados para o número de livros vieram de uma distribuição conhecida. Como essa variável assume valores em \({0,1,2,3}\), pode-se considerar, por exemplo, a distribuição Uniforme neste conjunto ou uma Binomial com \(n=3\).
Podemos escolher o \(p\) da Binomial lembrando que seu valor esperado é \(np=3p\) e igualando esse valor à média amostral \(\bar{x}=1.4\). Assim, podemos tomar \(p=1.4/3=7/15\).
# Gráfico de barras para o Número de Livros
tabela %>% ggplot() + theme_bw() +
geom_col(aes(x=Nlivros,y=FreqRel, color="Histograma"),fill="lightgreen") +
geom_point(aes(x=Nlivros,y=dbinom(Nlivros,size=3,prob=7/15),
color="Binomial(3,7/15)"),size=3) +
geom_point(aes(x=Nlivros,y=extraDistr::ddunif(Nlivros,min=0,max=3),
color="Uniforme{0,1,2,3}"),size=3) +
ylab("Frequência Relativa") + xlab("Número de Livros") +
labs(color = "Distribuição")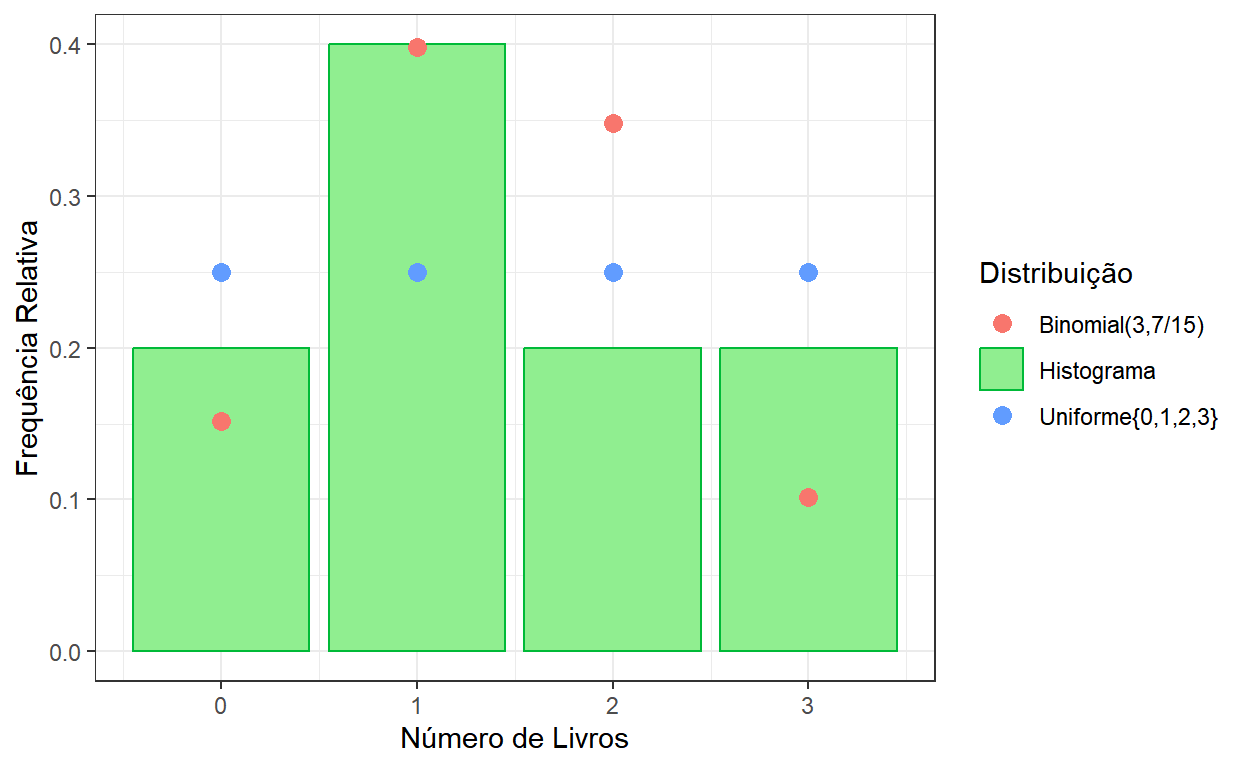
# Gráfico de barras para o Número de Livros
dados %>% ggplot() + theme_bw() + xlim(-0.5,3.5) +
stat_ecdf(aes(x=Nlivros, color="Empírica"),size=2) +
stat_function(aes(color="Binomial(3,7/15)"),
fun=pbinom,args=list(size=3,prob=7/15),
,size=1,n=2000) +
stat_function(aes(color="Uniforme{0,1,2,3}"),
fun=extraDistr::pdunif,args=list(min=0,max=3),
,size=1,n=2000) +
ylab("Função de Distribuição") + xlab("Número de Livros") +
labs(color = "Distribuição")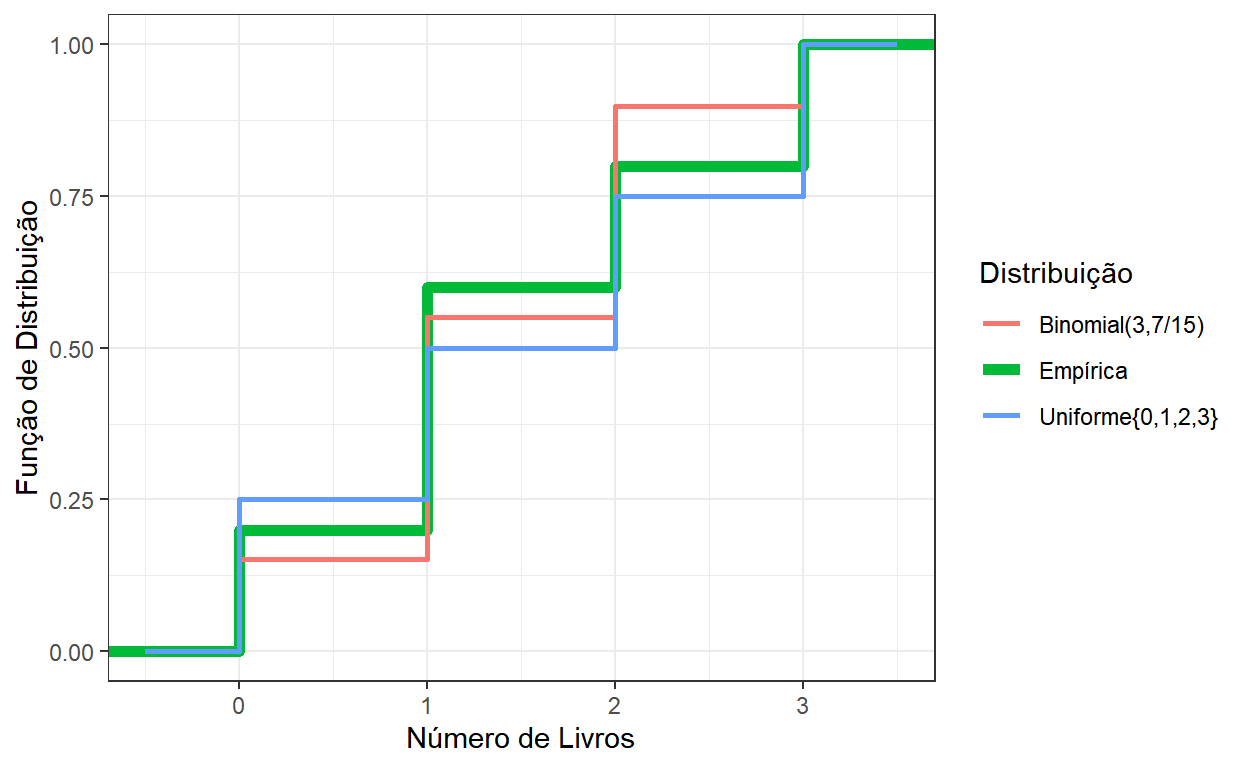
P-P Plot
Um outra forma visual de avaliar a semelhança entre duas distribuições são os gráfico do tipo P-P Plot.
Este gráfico é um gráfico de dispersão onde são plotados as funções de distribuição que deseja-se comparar, calculada nos pontos observados na amostra. Quanto mais os pontos se aproximam da reta \(y=x\), mais similares são as distribuições.
No exemplo anterior, vamos plotar os pares \(\left(~F_n(x_i)~,~F(x_i)~\right)\), \(i=1,\ldots,n\), em que \(F_n\) é a distribuição empírica obtida da amostra e \(F\) é uma função de distribuição acumulada teórica. No exemplo, tem-se \(F_U\) da distribuição \(Uniforme\{0,1,2,3\}\) e \(F_B\) da \(Binomial(3,7/15)\).
distr <- tabela %>%
mutate(Fu=extraDistr::pdunif(Nlivros,min=0,max=3),
Fb=pbinom(Nlivros,size=3,prob=7/15)) %>%
select(Nlivros,Fn,Fb,Fu)
distr %>%
kbl(align='c') %>%
kable_paper(bootstrap_options = "striped", full_width = T) %>%
row_spec(0, bold = T, color = "white", background = "#730217")| Nlivros | Fn | Fb | Fu |
|---|---|---|---|
| 0 | 0.2 | 0.1517037 | 0.25 |
| 1 | 0.6 | 0.5499259 | 0.50 |
| 2 | 0.8 | 0.8983704 | 0.75 |
| 3 | 1.0 | 1.0000000 | 1.00 |
distr %>% ggplot() + theme_bw() +
geom_point(aes(x=Fn,y=Fb,
color="Binomial(3,7/15)"),size=3) +
geom_point(aes(x=Fn,y=Fu,
color="Uniforme{0,1,2,3}"),size=3) +
geom_abline() +
ylab("Distribuição Teórica") + xlab("Distribuição Empírica") +
labs(color = "Distribuição")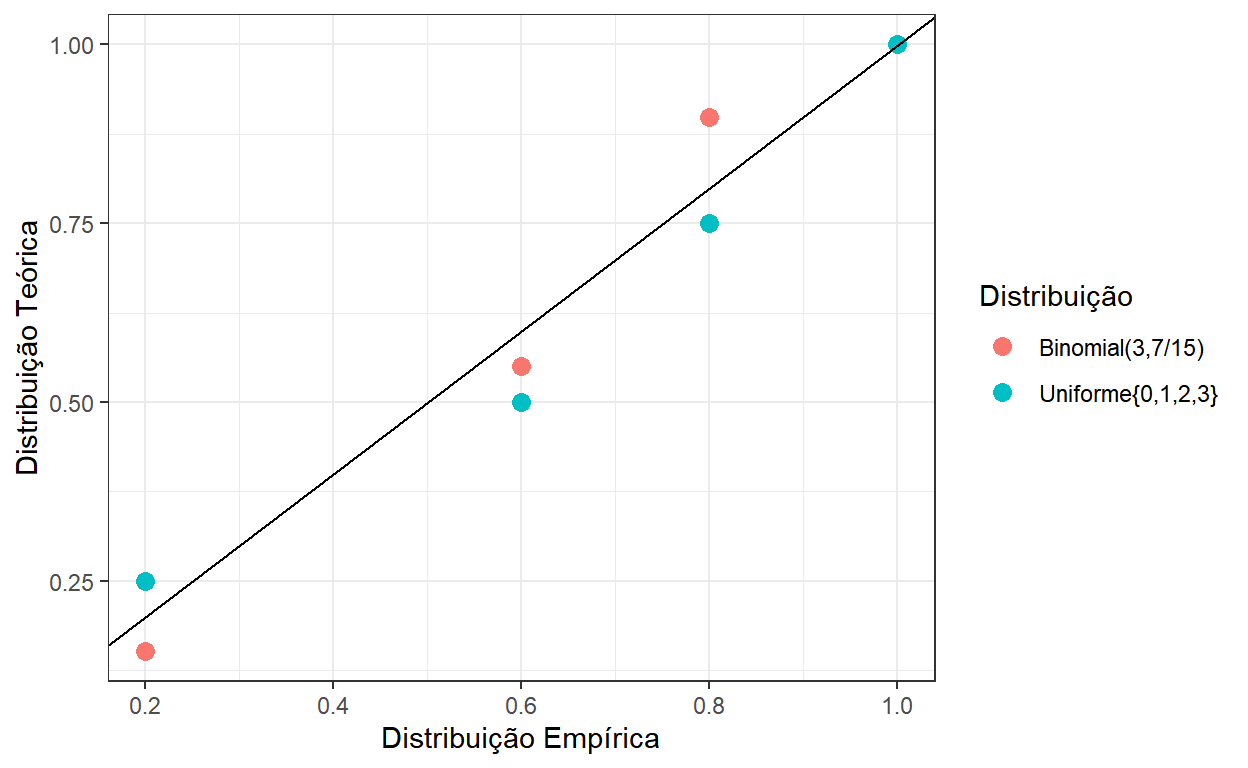
Medidas para a Comparação de Distribuições
- Existem diversas métricas para a comparação de distribuições. Aqui vamos discutir duas estatísticas, a já vista estatística de Qui-Quadrado e a estatística de Kolmogorov-Smirnov.
Esp <- tabela %>% select(Nlivros,FreqObs) %>%
mutate(Esp_Uniforme=10*extraDistr::ddunif(Nlivros,min=0,max=3),
Esp_Binomial=10*dbinom(Nlivros,size=3,prob=7/15))
Esp %>%
kbl(align='c') %>%
kable_paper(bootstrap_options = "striped", full_width = T) %>%
row_spec(0, bold = T, color = "white", background = "#730217")| Nlivros | FreqObs | Esp_Uniforme | Esp_Binomial |
|---|---|---|---|
| 0 | 2 | 2.5 | 1.517037 |
| 1 | 4 | 2.5 | 3.982222 |
| 2 | 2 | 2.5 | 3.484444 |
| 3 | 2 | 2.5 | 1.016296 |
- Qui-Quadrado: \(Q^2 = \sum_i \frac{(o_{i}-e_{i})^2}{e_{i}}\) ,
- em que \(o_i\) são as frequências observadas na amostra e \(e_i\) são as frequências esperadas se os dados tivessem sido gerados por uma determinada distribuição.
- \(e_i = n~\cdot~P(Y=x_i)\) , em que \(n\) é o total de observações na amostra e \(Y\) é uma variável aleatória com a distribuição que desejamos comparar.
- No exemplo, \(Q_U=\) 1.2 e \(Q_B=\) 1.738 são os valores da estatística de Qui-Quadrado para a comparação entre a distribuição dos dados com a Uniforme e a Binomial, respectivamente.
- em que \(o_i\) são as frequências observadas na amostra e \(e_i\) são as frequências esperadas se os dados tivessem sido gerados por uma determinada distribuição.
- Kolmogorov-Smirnov (K-S): \(\displaystyle D_n = \sup_{x_i}{\left|F_n(x_i)-F(x_i)\right|}\) ,
- em que \(F\) é a distribuição teórica.
- No exemplo, \(D_U=\) 0.1 e \(D_B=\) 0.098 são os valores da estatística K-S para a comparação entre a distribuição dos dados com a Uniforme e a Binomial, respectivamente.
- em que \(F\) é a distribuição teórica.
Regressão Linear Simples
- Considere uma amostra de duas variáveis (contínuas), \((x_1,y_1),(x_2,y_2),\ldots,(x_n,y_n)\), por exemplo, Altura e Peso.
dados %>% ggplot() + theme_bw() +
geom_point(aes(x=Altura, y=Peso), color="darkgreen", size=3)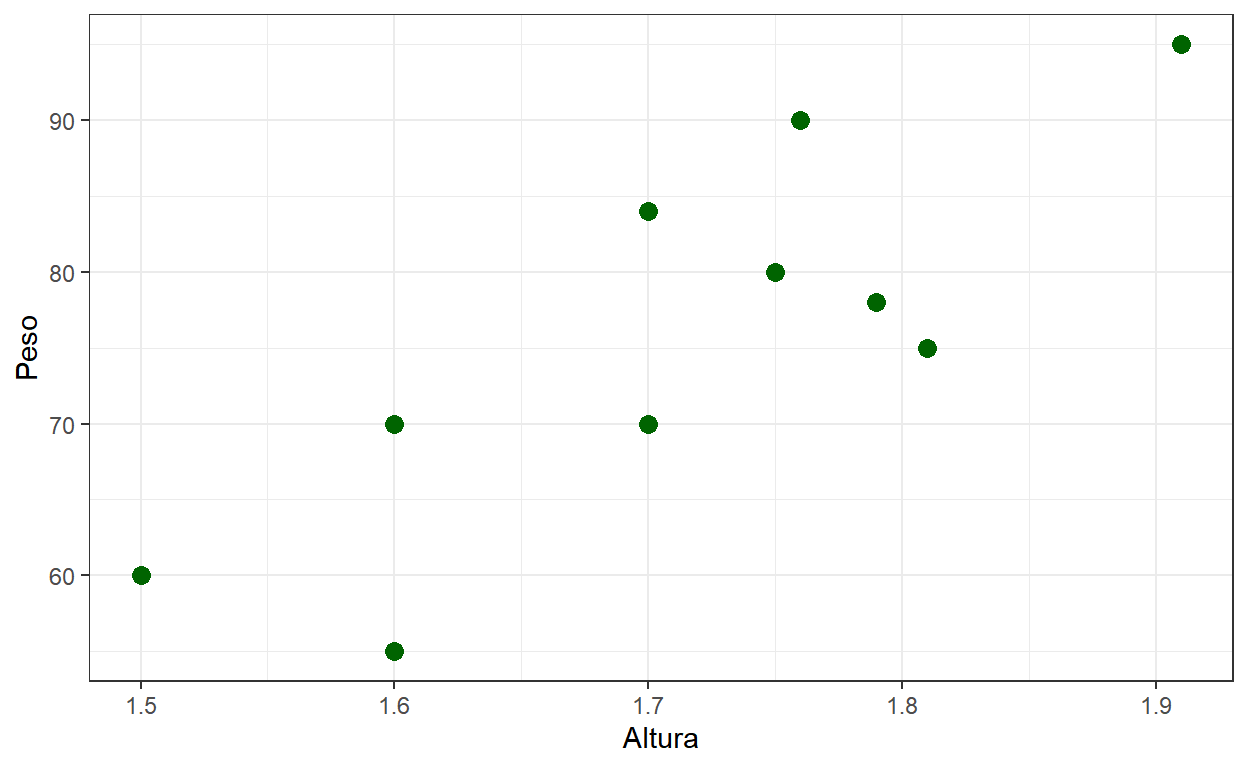
Suponha que é desejado obter a reta \(y=ax+b\) que “melhor aproxima” esses pontos. Para isso, é necessário definir o que significa “melhor aproxima”. Uma forma de fazer isso é considerar a soma de quadrados dos resíduos \[S = \sum_{i=1}^n r_i^2 = \sum_{i=1}^n \left[y_i-(ax_i+b)\right]^2\]
Os valores de \(a\) e \(b\) que minimizam a soma de quadrados dos resíduos (veja, por exemplo, esse link) são \[\hat{a}=\frac{\sum(x_i-\bar{x})(y_i-\bar{y})}{\sum(x_i-\bar{x})^2}~~\text{ e }~~ \hat{b}=\bar{y}-\hat{a}\bar{x}\]
No R, podemos ajustar esse modelo pelo comando
lm.
Call:
lm(formula = Peso ~ Altura, data = dados)
Residuals:
Min 1Q Median 3Q Max
-11.115 -4.599 1.702 3.524 10.192
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -70.81 36.45 -1.942 0.0880 .
Altura 85.58 21.25 4.028 0.0038 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 7.629 on 8 degrees of freedom
Multiple R-squared: 0.6698, Adjusted R-squared: 0.6285
F-statistic: 16.22 on 1 and 8 DF, p-value: 0.003799dados %>% ggplot(aes(x=Altura, y=Peso)) + theme_bw() +
geom_point(color="darkgreen", size=3) +
geom_smooth(method = "lm", se = FALSE)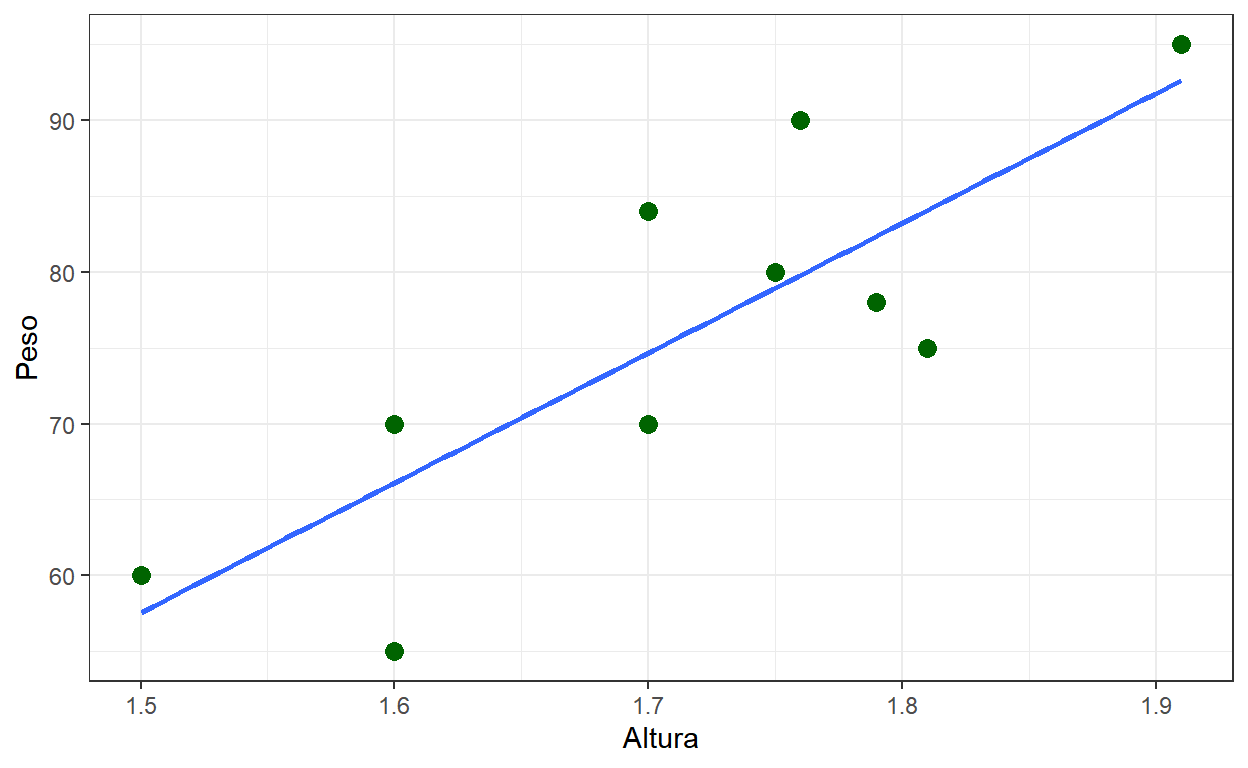
names(modelo) [1] "coefficients" "residuals" "effects" "rank"
[5] "fitted.values" "assign" "qr" "df.residual"
[9] "xlevels" "call" "terms" "model" tibble(obs=dados$Peso,ajust=modelo$fitted.values,
residuos=modelo$residuals) %>%
ggplot() + theme() +
geom_point(aes(obs,ajust), color="darkgreen", size=3) +
geom_abline(color="green", size=1)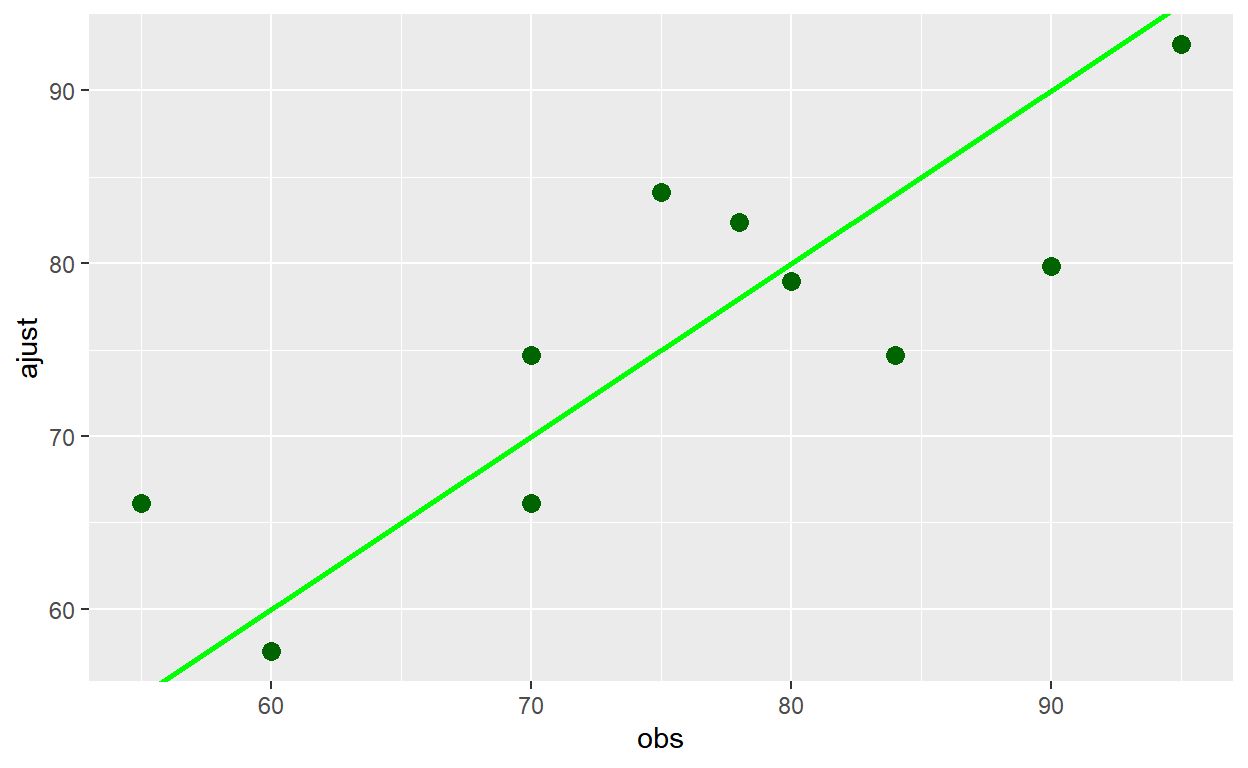
# Histograma + Boxplot para os resíduos
hist <- tibble(obs=dados$Peso,ajust=modelo$fitted.values,
residuos=modelo$residuals) %>% ggplot() + theme_bw() +
geom_histogram(aes(residuos,after_stat(density)),
color="black", fill="lightgreen",
bins=7) +
stat_function(fun=dnorm,color="red",size=1,n=2000,
args=list(mean=0,sd=summary(modelo)$sigma)) +
xlim(-11.5,11.5)
box <- tibble(obs=dados$Peso,ajust=modelo$fitted.values,
residuos=modelo$residuals) %>% ggplot() + theme_bw() +
geom_boxplot(aes(x=residuos,y=""),
color="black", fill="lightgreen") +
xlim(-11.5,11.5)
ggpubr::ggarrange(hist, box, heights = c(2, 1), nrow=2, align = "v")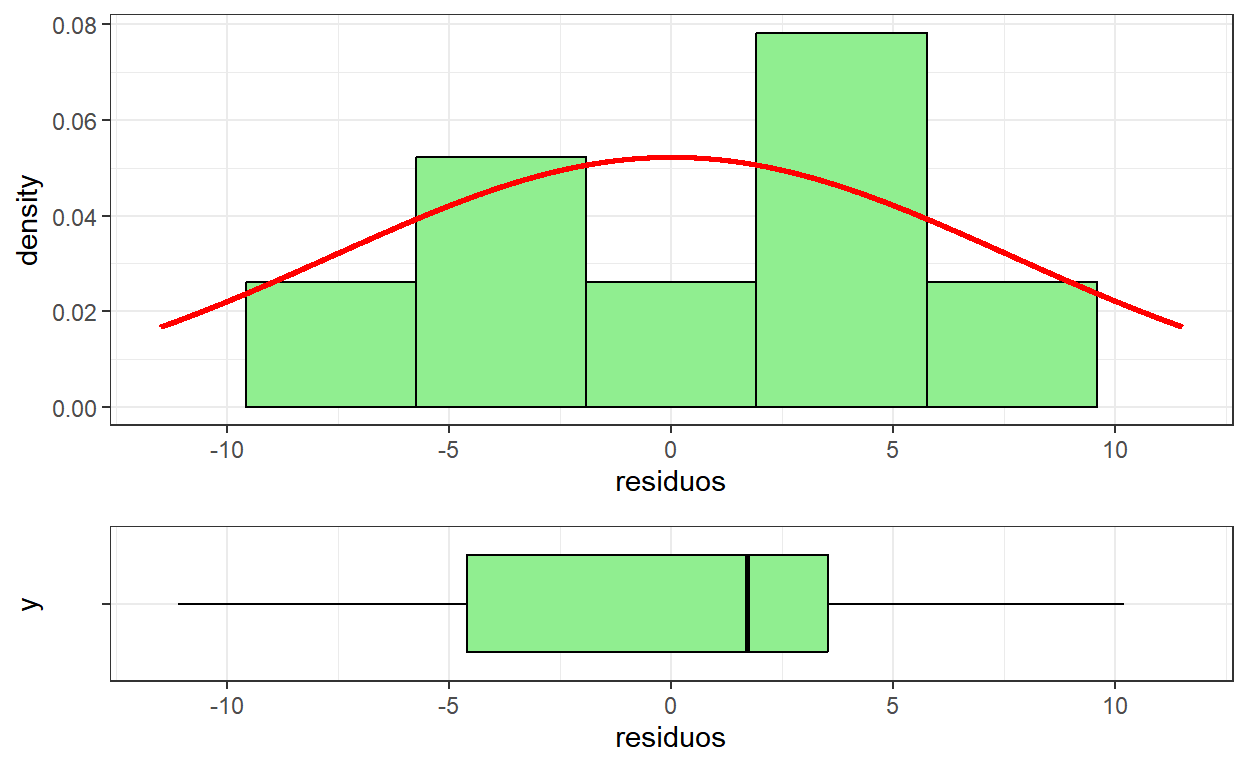
Análise de Resíduos
- Considere o exemplo de Regressão Linear que vimos anteriormente.
dados <- read_csv("dados\\exemplo_dados.csv")
dados %>% ggplot(aes(x=Altura, y=Peso)) + theme_bw() +
geom_point(color="darkgreen", size=3) +
geom_smooth(method = "lm", se = FALSE)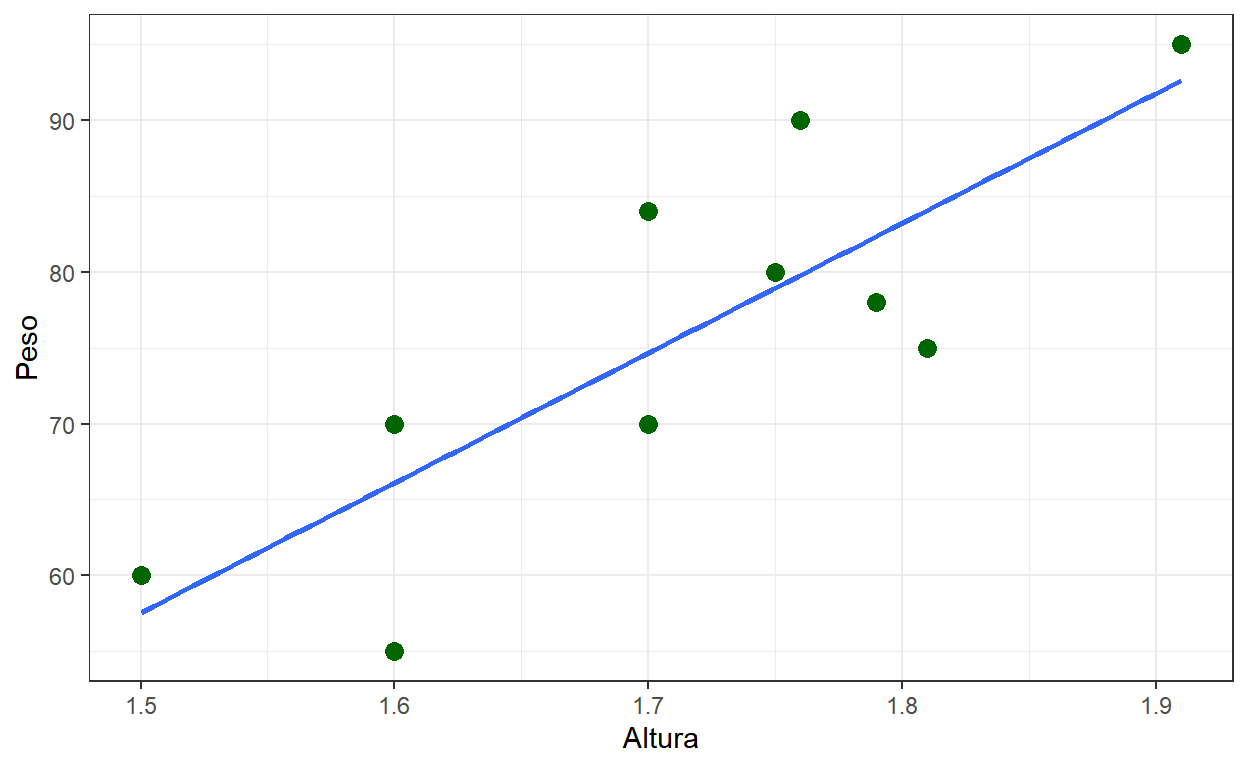
modelo <- lm(Peso~Altura, data=dados)
tbl_regression(modelo, intercept=T)| Characteristic | Beta | 95% CI | p-value |
|---|---|---|---|
| (Intercept) | -71 | -155, 13 | 0.088 |
| Altura | 86 | 37, 135 | 0.004 |
| Abbreviation: CI = Confidence Interval | |||
- Uma suposição usualmente feita em regressão é que os resíduos seguem uma distribuição normal.
# Histograma + Boxplot para os resíduos
hist <- tibble(obs=dados$Peso,ajust=modelo$fitted.values,
residuos=modelo$residuals) %>% ggplot() + theme_bw() +
geom_histogram(aes(residuos,after_stat(density)),
color="black", fill="lightgreen",
bins=5) +
stat_function(fun=dnorm,color="red",size=1,n=2000,
args=list(mean=0,sd=summary(modelo)$sigma)) +
xlim(-11.5,11.5) + xlab("")
box <- tibble(obs=dados$Peso,ajust=modelo$fitted.values,
residuos=modelo$residuals) %>% ggplot(aes(x=residuos,y="")) +
theme_bw() + xlim(-11.5,11.5) + ylab("") +
geom_boxplot(color="black", fill="lightgreen") +
ggbeeswarm::geom_beeswarm(cex=5,size=2,method = "center")
ggpubr::ggarrange(hist, box, heights = c(2, 1), nrow=2, align = "v")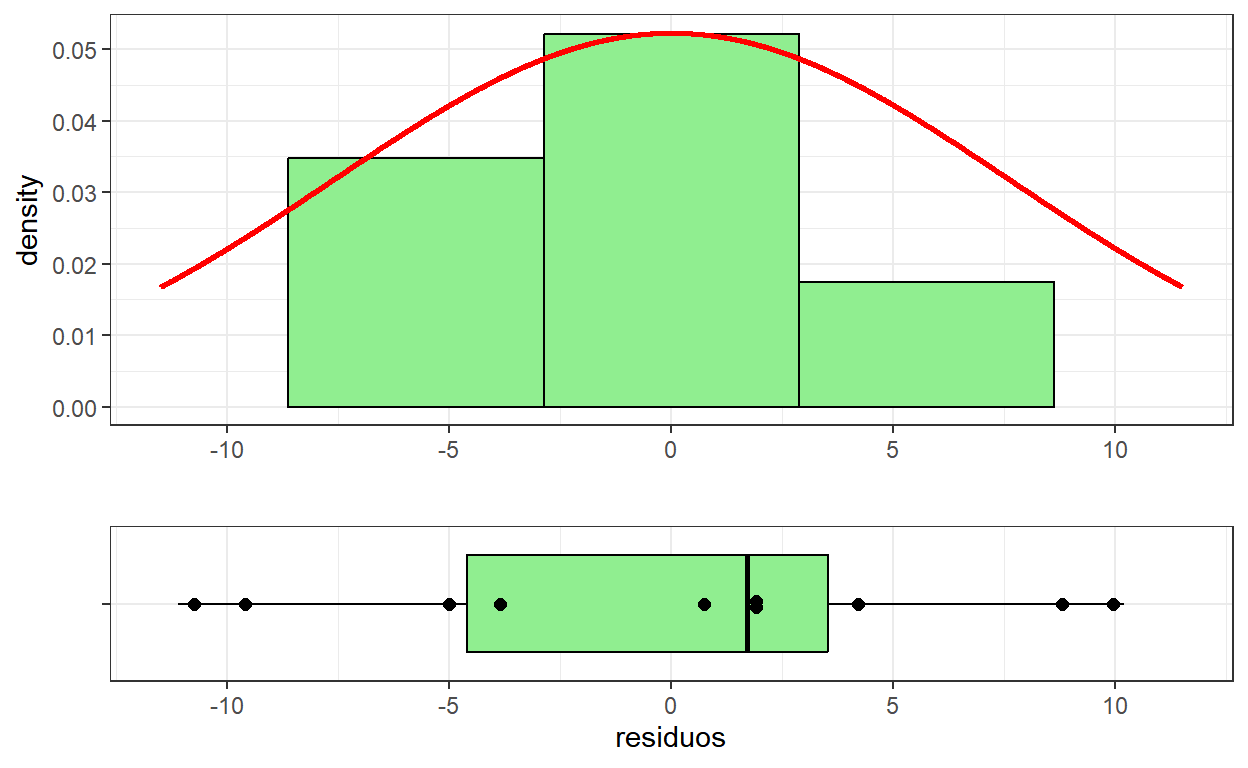
- Uma versão alternativa dos gráficos anteriores é apresentada a seguir.
# Densidade + Violin Plot para os resíduos
dens <- tibble(obs=dados$Peso,ajust=modelo$fitted.values,
residuos=modelo$residuals) %>% ggplot() + theme_bw() +
geom_density(aes(residuos,after_stat(density)),
color="black", fill="lightgreen") +
stat_function(fun=dnorm,color="red",size=1,n=2000,
args=list(mean=0,sd=summary(modelo)$sigma)) +
xlim(-15,15) + xlab("")
viol <- tibble(obs=dados$Peso,ajust=modelo$fitted.values,
residuos=modelo$residuals) %>% ggplot(aes(x=residuos,y="")) +
theme_bw() + xlim(-15,15) + ylab("") +
geom_violin(color="black", fill="lightgreen") +
ggbeeswarm::geom_beeswarm(cex=5,size=2,method = "center")
ggpubr::ggarrange(dens, viol, heights = c(2, 1), nrow=2, align = "v")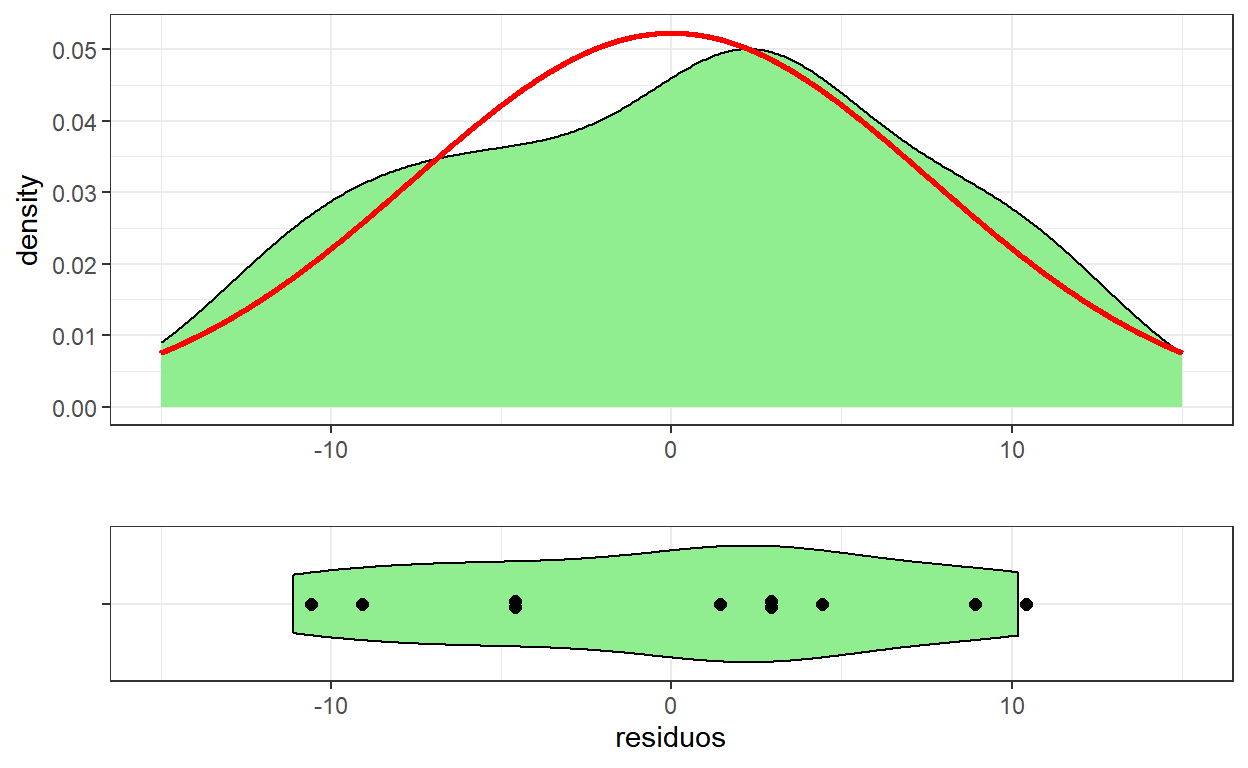
P-P Plot dos Resíduos
Assim como na aula passada, podemos fazer um gráfico do tipo P-P Plot para avaliar se a distribuição dos resíduos segue uma distribuição normal.
Neste gráfico são plotados os pares \(\left(~F_n(x_i)~,~F(x_i)~\right)\) , em que \(F_n\) é a função de distribuição empírica, \(F\) é a teórica e \(x_i\) são os pontos observados na amostra (no exemplo, os resíduos).
residuos <- tibble(residuos=sort(modelo$residuals)) %>%
mutate(Empirica=seq(1:length(residuos))/length(residuos),
Normal=pnorm(residuos,0,summary(modelo)$sigma))
residuos %>%
kbl(align='c', digits = 2) %>%
kable_paper(bootstrap_options = "striped", full_width = T) %>%
row_spec(0, bold = T, color = "white", background = "#730217")| residuos | Empirica | Normal |
|---|---|---|
| -11.12 | 0.1 | 0.07 |
| -9.09 | 0.2 | 0.12 |
| -4.67 | 0.3 | 0.27 |
| -4.38 | 0.4 | 0.28 |
| 1.05 | 0.5 | 0.55 |
| 2.36 | 0.6 | 0.62 |
| 2.44 | 0.7 | 0.63 |
| 3.88 | 0.8 | 0.69 |
| 9.33 | 0.9 | 0.89 |
| 10.19 | 1.0 | 0.91 |
residuos %>% ggplot() + theme_bw() +
geom_point(aes(x=Empirica,y=Normal),
color="darkgreen",size=3) +
geom_abline() +
ylab("Distribuição Normal") +
xlab("Distribuição Empírica dos Resíduos")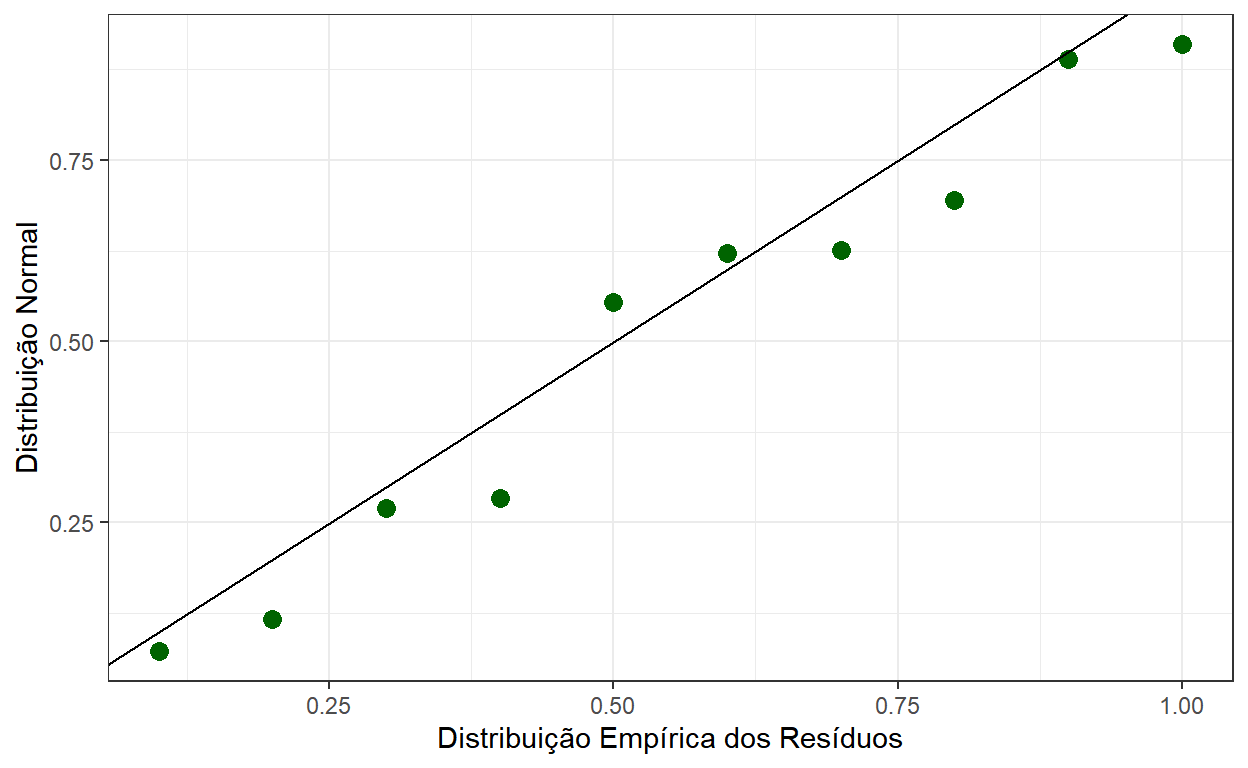
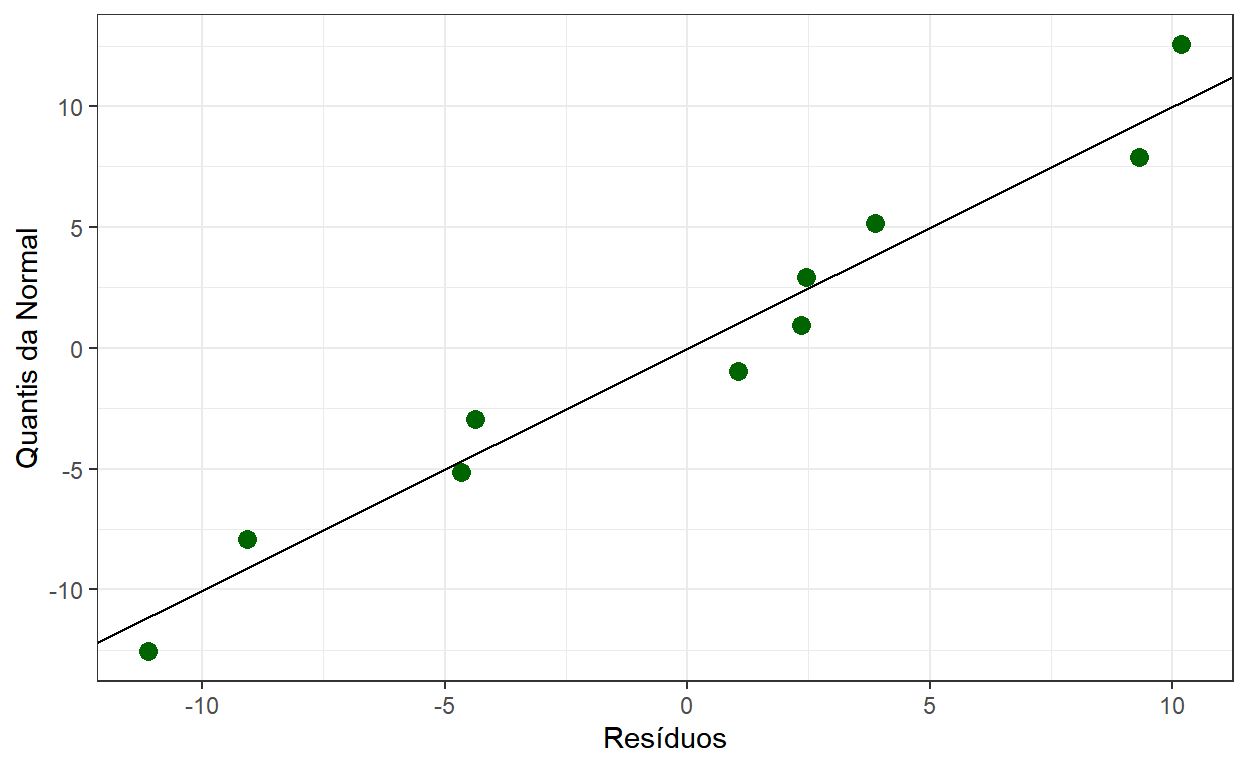
Q-Q Plot dos Resíduos
Uma alternativa mais usada que o gráfico anterior é o Q-Q Plot.
Neste gráfico, ao invés das probabilidades acumuladas da Normal, são plotados os resíduos e os quantis teóricos \(\left(~x_{(i)}~,~Q(p_i)~\right)\), em que \(x(i)\) são os valores observados ordenados, \(Q(p)\) é o quantil teórico de ordem \(p\) e as probabilidades \(p_i\) usualmente são calculadas como \(p_i=(i-0.5)/n\) ou \(p_i=i/(n+1)\).
residuos <- residuos %>%
mutate(pi=(seq(1:10)-0.5)/10,
qNormal=qnorm(Empirica-0.5/10,0,summary(modelo)$sigma))
residuos %>% select(residuos,pi,qNormal) %>%
kbl(align='c', digits = 2) %>%
kable_paper(bootstrap_options = "striped", full_width = T) %>%
row_spec(0, bold = T, color = "white", background = "#730217")| residuos | pi | qNormal |
|---|---|---|
| -11.12 | 0.05 | -12.55 |
| -9.09 | 0.15 | -7.91 |
| -4.67 | 0.25 | -5.15 |
| -4.38 | 0.35 | -2.94 |
| 1.05 | 0.45 | -0.96 |
| 2.36 | 0.55 | 0.96 |
| 2.44 | 0.65 | 2.94 |
| 3.88 | 0.75 | 5.15 |
| 9.33 | 0.85 | 7.91 |
| 10.19 | 0.95 | 12.55 |
residuos %>% ggplot() + theme_bw() +
geom_point(aes(x=residuos,y=qNormal),
color="darkgreen",size=3) +
geom_abline() +
ylab("Quantis da Normal") +
xlab("Resíduos")