O que significa algo ser “aleatório”?
- Aleatório (Google - Oxford Languages)
(adjetivo)
- que depende das circunstâncias, do acaso; casual, fortuito, contingente.
- (física) referente a fenômenos físicos para os quais as variáveis tomam valores segundo uma determinada lei de probabilidade (p.ex., o movimento browniano).
- Experimento Aleatório (The Concise Encyclopedia of Statistics, pp 430–433)
Um experimento em que o resultado não é previsível com antecedência é chamado de experimento aleatório. Um experimento aleatório pode ser caracterizado da seguinte forma:
1. É possível descrever o conjunto de todos os resultados possíveis (chamado espaço amostral do experimento aleatório).
2. Não é possível prever o resultado com certeza.
3. É possível associar cada resultado possível a uma probabilidade de ocorrência.
O que é Probabilidade?
- Probabilidade (Google - Oxford Languages)
(substantivo feminino)
- perspectiva favorável de que algo venha a ocorrer; possibilidade, chance.
“há pouca probabilidade de chuva”
- grau de segurança com que se pode esperar a realização de um evento, determinado pela frequência relativa dos eventos do mesmo tipo numa série de tentativas.
- Probabilidade (The Concise Encyclopedia of Statistics, pp 430–433)
Podemos definir a probabilidade de um evento usando as frequências relativas ou por meio de uma abordagem axiomática.
Na primeira abordagem, supomos que um experimento aleatório é repetido muitas vezes nas mesmas condições. Para cada evento \(A\) definido no espaço amostral \(\Omega\), definimos \(n_A\) como o número de vezes que o evento \(A\) ocorreu durante as primeiras \(n\) repetições do experimento. Neste caso, a probabilidade do evento \(A\), denotada por \(P(A)\), é definido por: \[P(A) = \lim_{n\rightarrow\infty} \frac{n_A}{n}~,\]
o que significa que \(P(A)\) é definido como o limite relativo ao número de vezes que o evento \(A\) ocorreu relativo ao número total de repetições.
Na segunda abordagem, para cada evento \(A\), aceitamos que existe uma probabilidade de \(A\), \(P(A)\), satisfazendo os três axiomas a seguir:
1. \(0\leq P(A)\leq 1\),
2. \(P(\Omega)=1\),
3. Para cada sequência de eventos mutuamente exclusivos \(A_1,A_2,\ldots\) (isto é, eventos tais que \(A_i \cap A_j = \emptyset\) se \(i \neq j\)):
\[ P\left(\bigcup_{i=1}^{\infty} A_i\right) = \sum_{i=1}^{\infty} P(Ai)~.\]
Interpretações de Probabilidade
- Interpretação Clássica (De Moivre, Laplace)
- baseia-se na equiprobabilidade dos resultados;
- \(P(A) = \frac{|A|}{|\Omega|}\).
- Exemplo: um lançamento de moeda, \(A\) = “cara”, \(P(A) = \frac{1}{2}\).
\(~\)
- Interpretação Frequentista (Venn, von Mises, Reichenbach, etc.)
- quase unânime na primeira metade do século XX e ainda é a mais aceita;
- baseia-se na regularidade das frequências relativas (lei dos grandes números);
- \(P(A) = lim \frac{A_n}{n}\), onde \(A_n\) é o número de ocorrências de \(A\) em \(n\) realizações idênticas e independentes do experimento;
- Supõe que é possível repetir indefinidamente o experimento nas mesmas circustâncias.
- Exemplo: um lançamento de moeda, \(A\) = “cara”.
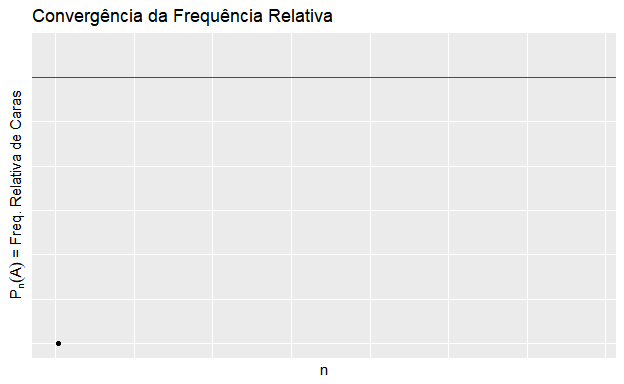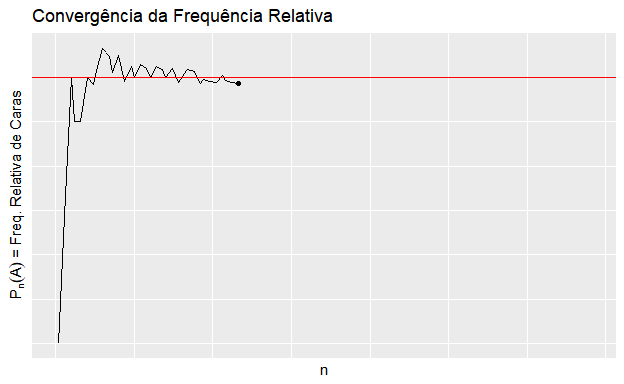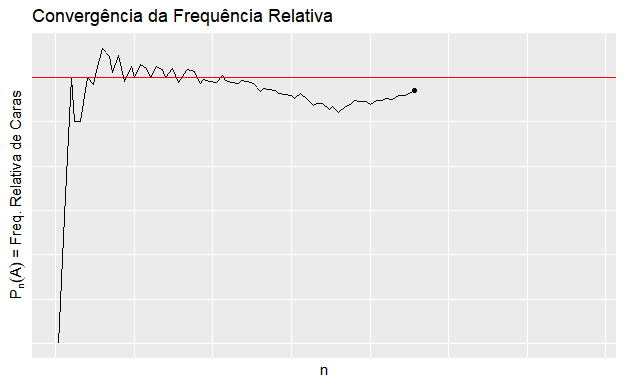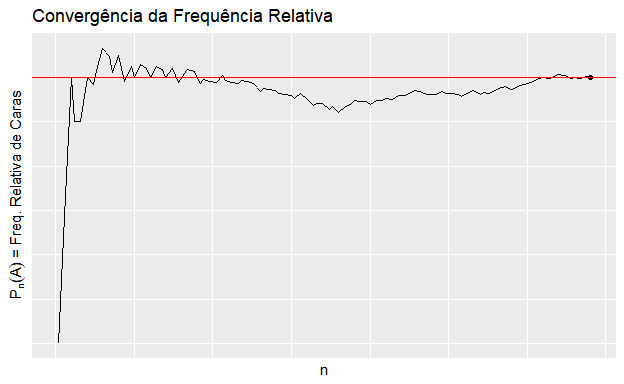
\(~\)
- Interpretação Subjetivista (Ramsey, de Finetti, Savage, etc)
- probabilidade como medida subjetiva de crença;
- baseada na experiência de cada indivíduo, portanto única.
- Exemplo: suponha que Bruno lançou uma moeda 3 vezes e todos os resultados foram cara. Esse indivíduo, em posse dessa informação, pode acreditar que o resultado cara é mais provável que coroa. Contudo, quando pergunta sobre a probabilidade de cara ao seu colega Olavo, ignorante com relação a moeda, ele responde que é 1/2.
Comentários sobre Probabilidade e Aleatoriedade
Exemplo da moeda. Aleatoriedade é uma característica (física) do lançamento da moeda?
Exemplo das bolas na Urna. A “aleatoriedade” está em “chacoalhar” a urna? E se eu “embrulhar” as bolas e colocá-las em fila sobre a mesa? O experimento ainda é “aleatório”? Qual a “probabilidade” de selecionar uma bola verde?
O que é Estatística?
- Estatística (Google - Oxford Languages)
(substantivo feminino)
- ramo da matemática que trata da coleta, da análise, da interpretação e da apresentação de massas de dados numéricos.
- qualquer coleta de dados quantitativos.
- Estatística (The Concise Encyclopedia of Statistics, pp 518–520)
A palavra estatística, derivada do latim, refere-se à noção de estado (status): “que é relativo ao estado”. Os governos têm uma grande necessidade de contar e medir numerosos eventos e atividades, como mudanças demográficas, nascimentos, tendências de imigração e emigração, mudanças nas taxas de emprego, negócios, etc.
Nessa perspectiva, o termo “estatística” é usado para indicar um conjunto de dados disponíveis sobre um determinado fenômeno (por exemplo, estatísticas de desemprego).
No sentido mais moderno e preciso da palavra, “estatística” é considerada uma disciplina que se preocupa com dados quantitativos. É constituído por um conjunto de técnicas de obtenção de conhecimento a partir de dados incompletos, de um rigoroso sistema científico de gestão de coleta de dados, da sua organização, análise e interpretação, quando é possível apresentá-los de forma numérica.
Numa população de indivíduos, pode ser de interesse saber, em termos de teoria estatística, se um determinado indivíduo tem carro ou se fuma. Por outro lado, também pode ser de interesse saber quantos indivíduos têm automóvel e são fumantes, e se existe relação entre possuir automóvel e hábitos de tabagismo na população estudada.
Gostaríamos de conhecer as características da população globalmente, sem nos preocuparmos com cada pessoa ou cada objeto da população.
Distinguimos dois subconjuntos de técnicas: (1) aquelas que envolvem estatísticas descritivas e (2) aquelas que envolvem estatísticas inferenciais. O objetivo essencial da estatística descritiva é representar a informação em um formato compreensível e útil. A estatística inferencial, por outro lado, visa facilitar a generalização dessas informações ou, mais especificamente, fazer inferências (relativas a populações) com base em amostras dessas populações.
- Estatístico (segundo prof. Carlos Alberto de Bragança Pereira)
“The Statistician is the Wizard who makes”scientific” statements about invisible states and quantities. However, contrary to the real wishes (or witches), he attaches uncertainties to his statements.”
Comentários sobre Estatística
- Revisitando o exemplo da Urna quando não se sabe sua composição.
Método Científico
- Formulação de uma questão, teoria ou hipótese.
- Coleta de informações: planejamento de um experimento para obtenção de dados ou apenas a observação de um fenômeno ou variáveis de interesse.
- Conclusões (por vezes, parciais) baseadas nos dados obtidos anteriormente.
- Se necessário, repetir (2) e (3) ou formular novas hipóteses.
População X Amostra, Probabilidade X Estatística
População é o conjunto de todos os elementos ou resultados possíveis.
Amostra é um subconjunto da população.
Experimento é “tornar visível o que antes era invisível”, por exemplo, observar uma amostra da população.
Probabilidade é uma descrição matemática da incerteza, é bem especificada quando a população é conhecida.
Estatística estuda a distribuição de probabilidades quando esta não está bem especificada (é desconhecida, ao menos parcialmente).
- Modelo Probabilístico: \((\Omega, \mathcal{F}, \boldsymbol{P})\), onde \(\Omega\) é o espaço amostral, \(\mathcal{F}\) é uma coleção (\(\sigma\)-álgebra) de subconjuntos de omega e \(\boldsymbol{P}\) é uma medida de probabilidade (conhecida, fixada)
- Modelo Estatístico: simplificadamente, um modelo estatístico é uma forma probabilística de relacionar uma quantidade desconhecida de interesse (parâmetro) com os dados observados.
- \((\Omega, \mathcal{F}, \mathcal{P})\), onde \(\mathcal{P}\) é uma família de distribuições de probabilidade. Na estatística, o objetivo é fazer afirmações sobre essa família.
- Modelo Probabilístico: \((\Omega, \mathcal{F}, \boldsymbol{P})\), onde \(\Omega\) é o espaço amostral, \(\mathcal{F}\) é uma coleção (\(\sigma\)-álgebra) de subconjuntos de omega e \(\boldsymbol{P}\) é uma medida de probabilidade (conhecida, fixada)
Exemplos: urna quando sua composição não é conhecida, moeda quando não se sabe a probabilidade de cara.
Discussão sobre independência probabilística e estatística.
Estatística Descritiva
- Conjunto de técnicas para visualização (redução) dos dados.
- Análises e conclusões preliminares.
- Fornece informações que auxiliam na especificações de um modelo estatístico.
- Também utilizada para
- Avaliação de modelos;
- Interpretação de modelos complexos;
- Comunicação dos resultados.
- Avaliação de modelos;
- Exemplo: medidas resumo, gráficos e tabelas.
Inferência Estatística
- Generalizar resultados observados em uma amostra para a população de interesse.
- Normalmente baseada em algumas suposições que são traduzidas em um modelo estatístico.
- Principais objetivos: concluir se há relações entre variáveis, estimativas pontuais e intervalares e testes de hipóteses.
- Como o objetivo é generalizar conclusões para a população, é usual ter uma grande preocupação com a verificação das suposições do modelo estatístico adotado.
- Por vezes chamada de “análise confirmatória”.
Aprendizado Estatístico
- Similarmente à inferência estatística, estuda relação entre variáveis mas tem como objetivo fazer predições para novas observações.
- Como o objetivo é fazer predições, o foco é obter um modelo que “acerte” mais ou, em outras palavras, que minimize algum tipo de função de perda, dando menos atenção à suposições sobre o modelo probabilístico utilizado.
- Na prática, o conjunto de dados é dividido em um conjunto de treinamento e um conjunto de teste. O primeiro é usado para a obtenção de modelos e o segundo para a sua avaliação. O modelo escolhido é aquele que “acerta mais” no conjunto de teste.
- Também pode ser pensada como uma forma reproduzir o mecanismo gerador dos dados.