next up previous
Next: About this document ...

Primeira Lista de L�gica Fuzzy




Cursos de Ver�o IME-USP - 2002




1. D� alguns exemplos de afirma��es em linguagem natural que envolvem conceitos nebulosos (fuzzy).



2. Descreva situa��es de sua experi�ncia pessoal onde s�o necess�rios conceitos nebulosos.



3. Usando apenas o senso comum, defina algumas fun��es de pertin�ncia para os seguintes conjuntos nebulosos.

(a) $ n$ � grande.

(b) A m�dia de uma vari�vel aleat�ria � aproximadamente 5

(c) $ x$ � muito maior que $ y$.

(d) O vento est� forte.

(e) $ x$ est� entre -3 e 2



4. Seja $ U=\{0, 1, 2, 3, 4, 5, 6, 7, 9\}$. Sejam $ A$ e $ B$ dois subconjuntos nebulosos de $ U$ dado pelas fun��es de pertin�ncias:

$ u$ 0 1 2 3 4 5 6 7 8 9
$ A(u)$ 0 0 0.1 0.2 0.3 0.8 0.9 1 1 1
e

$ u$ 0 1 2 3 4 5 6 7 8 9
$ B(u)$ 1 1 0.9 0.8 0.7 0.5 0.4 0.2 0.2 0

Determine $ A \wedge B$, $ A \vee B$ e $ A^{\prime}$.



5. Sejam $ A$ e $ B$ dois subconjuntos nebulosos do conjunto dos n�meros reais n�o negativos, ache novamente $ A \wedge B$, $ A \vee B$ e $ A^{\prime}$ quando:

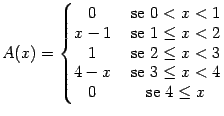
$\displaystyle A(x) = \left\{ \begin{matrix} 0 & \text{ se } 0<x<1 \\ x-1& \te... ... 4-x & \text{ se } 3\leq x< 4 \\ 0 & \text{ se } 4\leq x \end{matrix}\right. $

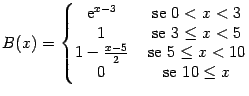
$\displaystyle B(x) = \left\{ \begin{matrix} \text{e}^{x-3} & \text{ se } 0<x<3... ...{2} & \text{ se } 5\leq x <10 \\ 0 & \text{ se } 10\leq x \end{matrix}\right. $

Fa�a os gr�ficos de todos estes conjuntos nebulosos.



6. Seja $ \{ A_1, A_2, \dots, A_n\}$ uma parti��o fuzzy de um conjunto $ U$. Verifique que se $ A_i$ s�o conjuntos cl�ssicos ent�o eles s�o dois a dois disjuntos e sua reuni�o � o conjunto inteiro $ U$. Se $ A$ � um conjunto nebuloso, ser� que $ A$ e $ A^{\prime}$ formam uma parti��o fuzzy?



7. Seja $ U=[0,10]$, verifique em cada caso se os conjuntos dados formam uma parti��o fuzzy de $ U$. Fa�a os gr�ficos.

(a) $ A_1(x)=\frac{x}{10}$ e $ A_2(x)=1-\frac{x}{10}$.

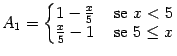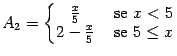
(b) $ A_1=\left\{ \begin{matrix} 1-\frac{x}{5} & \text{ se } x<5 \\ \frac{x}{5}-1 & \text{ se } 5\leq x \end{matrix}\right.$, $ A_2=\left\{ \begin{matrix} \frac{x}{5} & \text{ se } x<5 \\ 2- \frac{x}{5} & \text{ se } 5\leq x \end{matrix}\right.$

(c) $ A_1(x)=\sin^2(x)$, $ A_2=\cos^2(x)$

(d) $ A_1(x)=\frac{x}{30}$, $ A_2(x)=\frac{x^2}{100}$, $ A_3(x)=1-\frac{x}{10}$


next up previous
Next: About this document ...
Pedro A Tonelli
2002-01-07