 __________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________
Lista de exercícios de MAP2321  __________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________
Entregar a lista resolvida em 7 dias
1. Achar os resíduos nos pólos das seguintes funções:
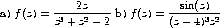
2. Calcular 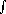
 f(z)dz quando:
f(z)dz quando:
![{
--1--- t se t (- [- 2,2]
f(z) = z4 + 1 e G(t) = 2e2pi(t-22) se t (- [2,3]](tecon05-42x.gif)
e quando
![-z +-1- 2pit
f (z) = sin(2z) e G(t) = 5e ,t (- [0,1]](tecon05-43x.gif)
3. Explique como podemos calcular a integral imprópria 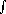 -
-
 dx__
x4+1 usando integração
complexa.
dx__
x4+1 usando integração
complexa.
4. O Teorema de Rouché diz o seguinte: Se f : 

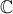 e
e  :
: 

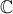 são duas funções
analíticas no domínio
são duas funções
analíticas no domínio  e
e  é uma curva simples fechada contida em
é uma curva simples fechada contida em  tal que f e
tal que f e  sejam
analíticas no interior de
sejam
analíticas no interior de  e sobre a curva temos a desigualdade |f(z)| > |phi(z)|. Então f(z) e
f(z) + phi(z) têm a mesma quantidade de zeros no interior de
e sobre a curva temos a desigualdade |f(z)| > |phi(z)|. Então f(z) e
f(z) + phi(z) têm a mesma quantidade de zeros no interior de  .
.
Dê uma prova do teorema de Rouché usando o princípio do argumento. E aplique este resultado para determinar quantos zeros de p(z) = z8 - 4z5 + z2 - 1 tem módulo estritamente menor que 1.