Séries, limite, integração, derivação, equações diferenciais, inequações, Simplex
Routo Terada
Somatória e produtória
> soma:=Sum( (1+i)/(1+i^4), i=1..10 );
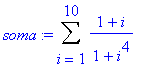
>
soma:=sum( (1+i)/(1+i^4), i=1..10 );
# note: sum com s em minúsculo
![]()
> evalf( soma, 50 );
![]()
>
soma:=Sum( (1+i)/(1+i^4), i=1..N );
produto:=Product( (1+i)/(1+i^4), i=1..N );
plot({produto,soma},N=1..10,thickness=3,color=[red,blue]);
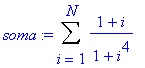
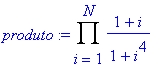
![[Maple Plot]](images/apost46.gif)
> produto:=Product( ((i^2+3*i+2)/(i+30)), i=1..10 );
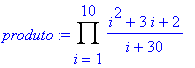
> value(produto);
![]()
> evalf( produto, 50 );
![]()
>
produto:=Product( ((i^2+3*i+2)/(i+30)), i=1..N);
soma:=Sum( ((i^2+3*i+2)/(i+30)), i=1..N);
plot({produto,soma},N=1..10,thickness=3,color=[red,blue]);
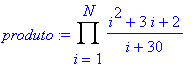
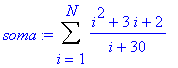
![[Maple Plot]](images/apost412.gif)
Integração e derivação
>
restart;
F:=f(x)*g(x); diff(F,x);
# regra de derivação de produto
![]()
![]()
>
F:=f(x)/g(x); diff(F,x);
# regra de derivação de divisão
![]()
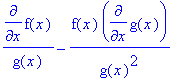
> F:=ln(1+x^2);
![]()
> plot(F,x=-1..1,thickness=3);
![[Maple Plot]](images/apost418.gif)
>
Integr:=Int(F,x=-1.5..1);
# note: Int com I em maiúsculo
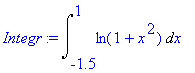
>
Integr:=int(F,x); IntegrDef:=evalf(int(F,x=-1..1));
# integral definida de -1 a 1
![]()
![]()
> plot({F,Integr,IntegrDef},x=-1..1,thickness=4,color=[green,blue,red]);
![[Maple Plot]](images/apost422.gif)
> Deriv:=diff(F,x); # derivação
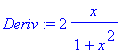
> plot({F,Deriv},x=-1..1,thickness=3,color=[blue,red]);
![[Maple Plot]](images/apost424.gif)
> Deriv2:=diff(F,x,x); # derivada segunda de F
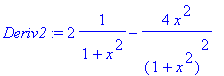
> plot({F,Deriv,Deriv2},x=-1..1,thickness=3,color=[blue,red,green]);
![[Maple Plot]](images/apost426.gif)
> restart;f := x -> x*sin(a*x) + b*x^2;
![]()
>
value(Diff( f(x), x ) );
deriv:=diff( f(x), x );
![]()
![]()
> f_linha := value(deriv);
>
![]()
> integral:=int(f_linha, x);
![]()
> simplify(integral);
>
![]()
>
Int( f_linha, x=1..2 );
integral:=int( f_linha, x=1..2 );
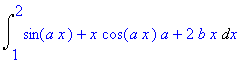
![]()
> value(integral);
>
![]()
> Int( 1/sqrt( 1 + x^4 ) , x=0..1 );
> integral:=int( 1/sqrt( 1 + x^4 ) , x=0..1 );
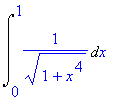
![]()
> value(integral); # integral elíptica
>
![]()
> evalf(integral);
>
![]()
Integral Dupla
>
F:=ln(1+x^2)*y^3+ln(y^2+3);
Fint:=Int(F,x);
![]()
![]()
> FintDup:=Int(Fint,y);
![]()
> Fint:=int( F , x);
![]()
> FintDup:=int( Fint , y );
![]()
>
plot3d({F,Fint},x=-10..10,y=0..10,thickness=3,shading=ZHUE,axes=boxed);
plot3d({Fint,FintDup},x=-10..10,y=0..10,thickness=3,shading=ZHUE,axes=boxed);
![[Maple Plot]](images/apost445.gif)
![[Maple Plot]](images/apost446.gif)
> Fint:=int( F , x=0..1 ); # integral definida
![]()
>
> FintDup:=int( Fint , y=0..1 ); evalf(FintDup);
![]()
![]()
Limite de expressões
> expr := (2*x+3)/(7*x+5);
![]()
> limite:=Limit( expr, x=infinity );
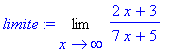
> value(limite);
>
![]()
>
limite:=Limit( tan(x+Pi/2), x=0, left );value(limite);
# limite da esquerda
>
![]()
![]()
>
limite:=Limit( tan(x+Pi/2), x=0, right );value(limite);
# limite da direita
>
![]()
![]()
> limite:=Limit( abs(x-4)/(x-4) , x=4, right ); # contendo abs
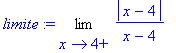
> value(limite);
>
![]()
>
l:=limit( sqrt(1-cos(x)) / x*sqrt(2), x=0 ); # lim indefinido
lesq:=limit( sqrt(1-cos(x)) / x*sqrt(2), x=0, left ); # lim da esquerda
![]()
![]()
>
>
>
>
Integração e derivação de funções definidas por partes
> p := x -> piecewise( x<0, -1, x>1, 2*x, x^2 );
![]()
> p(x);
![PIECEWISE([-1, x < 0],[2*x, 1 < x],[x^2, otherwise]...](images/apost462.gif)
> p_linha := diff( p(x), x );
![p_linha := PIECEWISE([0, x < 0],[undefined, x = 0],...](images/apost463.gif)
> expr := piecewise( x<=-1, -x, x<=1, x*x, x>1, sin(x-1)/(x-1) );
![expr := PIECEWISE([-x, x <= -1],[x^2, x <= 1],[sin(...](images/apost464.gif)
>
anti := int( expr, x ); # integral
valor :=evalf(1/6+Si(5.66-1));
#OBS:Si(x) é a Função Integral Seno, Si(x)=int(sin(t)/t, t=0..x)
![anti := PIECEWISE([-1/2*x^2, x <= -1],[1/3*x^3-1/6,...](images/apost465.gif)
![]()
Série e expansão em série
>
expr := sin(4*x)*cos(x):
approx1 := series( expr, x=0 );
![]()
> poly1 := convert( approx1, polynom ); # tranformar p/ polinômio
![]()
> plot( [expr, poly1], x=-1..1, title = `Aproxim. p/ Series` ); # p/ comparar original com a aproximação, em gráfico
![[Maple Plot]](images/apost469.gif)
> Order := 13; # muda a ORDEM de aproximação
![]()
> approx2 := series( expr, x=0 );
![]()
>
poly2 := convert( approx2, polynom );plot( [expr, poly2], x=-1..1,`Aproxim. p/ Series` );
![]()
![[Maple Plot]](images/apost473.gif)
> poly2fs := 4*x-38/3*x^3+421/30*x^5-10039/1260*x^7+246601/90720*x^9-6125659/9979200*x^11;
![]()
>
>
Equações diferenciais
Definir uma equação:
eq:=t^2*diff(x(t),t$2)-t*diff(x(t),t)+x(t)=0;
Note t$2 para indicar derivada segunda.
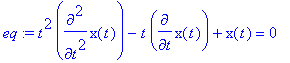
>
sol:=dsolve(eq,x(t));
dsolve() para resolver.
![]()
Para verificar a solução acima, usar subs():
simplify(subs(sol,lhs(eq))); # lhs indica Left Hand Side
![]()
>
eq2:=t^2*diff(x(t),t$2)-2*t*diff(x(t),t)+4*x(t)=11;
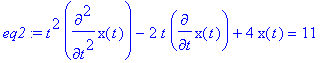
>
sol2:=dsolve(eq2,x(t));
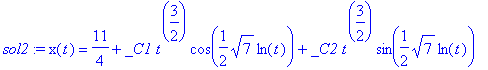
> simplify(sol2);
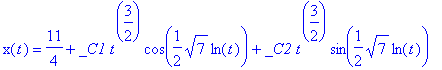
Para verificar a solução acima, usar subs():
simplify(subs(sol2,lhs(eq2)));
![]()
Equação diferencial com condição inicial:
eq3:=diff(x(t),t)+3*t*x(t)=0;
![]()
> dsolve( {eq3, x(0)=1}, x(t));
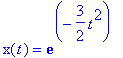
Condição inicial para a derivada é indicada com D()
:
eq4:=diff(x(t),t$2)-2*x(t)=0;
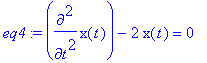
> dsolve( {eq4, x(0)=1,D(x)(0)=0}, x(t));
![]()
> dsolve( {eq4, x(0)=1,D(x)(0)=1}, x(t));
![]()
Equação com condição inicial para a segunda derivada
:
eq5:=diff(x(t),t$2)-cos(t)=0;
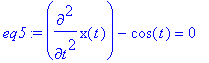
>
dsolve( {eq5, x(0)=1,(D@@2)(x)(0)=1}, x(t));
Notação D@@2
dsolve( {eq5, x(0)=1,D(D(x))(0)=1}, x(t));
Notação D(D(x))
![]()
![]()
Sistema de equações diferenciais lineares.
eq6a:=diff(x(t),t)-2*x(t)+5*y(t)=0;
eq6b:=diff(y(t),t)-x(t)+2*y(t)=0;
![]()
![]()
> inic1:=x(0)=0; inic2:=y(0)=1;
![]()
![]()
> dsolve({eq6a,eq6b,inic1,inic2},{x(t),y(t)});
![]()
Solução numérica de sistema de equações diferenciais (Equações de Lorenz)
>
eqa:=diff(x(t),t)-3*(y(t)-x(t))=0;
eqb:=diff(y(t),t)-30*x(t)+y(t)+x(t)*z(t)=0;
eqc:=diff(z(t),t)-x(t)*y(t)+z(t)=0;
![]()
![]()
![]()
> inic1:=x(0)=0; inic2:=y(0)=1;inic3:=z(0)=0;
![]()
![]()
![]()
>
>
sol:=dsolve({eqa,eqb,eqc,inic1,inic2,inic3},{x(t),y(t),z(t)},numeric):
# Note a opção numeric
> s2:=sol(2);
![]()
> with(plots): odeplot(sol,[x(t),y(t),z(t)],0..25,numpoints=1000,axes=boxed);
Warning, the name changecoords has been redefined
![[Maple Plot]](images/apost4102.gif)
Equação diferencial não-linear: (Cauchy-Euler)
> eqNL:=diff(x(t),t$2)+0.1*diff(x(t),t)+sin(x(t))=0.02*cos(t);
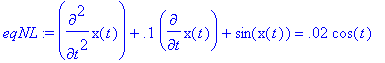
Primeiro convertemos esta equação para um sistema de equações de primeira ordem:
>
eqa:=diff(x(t),t)=y(t);
eqb:=diff(y(t),t)=-0.1*y(t)-sin(x(t))+0.02*cos(t);
![]()
![]()
> inic1:=x(0)=0;inic2:=y(0)=1;
![]()
![]()
Agora a solução do sistema equivalente à equação não-linear:
>
sol:=dsolve({eqa,eqb,inic1,inic2},{x(t),y(t)},numeric):
# sol() é uma função de t
> s2:=sol(2); # solução numérica no ponto t=2
![]()
A seguir um gráfico da solução no espaço de fases:
> with(plots): odeplot(sol,[x(t),y(t)],0..25,numpoints=1000,axes=boxed);
![[Maple Plot]](images/apost4109.gif)
Para obter solução em forma de série infinita
:
eq7:=diff(x(t),t$2)-t*x(t)=0;
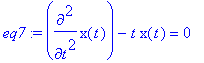
> Order:=12;dsolve(eq7, x(t), series); # default é Order=8
![]()
![]()
Com condições iniciais:
> dsolve( {eq7, x(0)=1, D(x)(0)=2}, x(t), series);
![]()
Equações diferenciais parciais (pdsolve())
>
restart;with(PDEtools):
eq:=(1+x^2)*diff(u(x,y),x)-y^2*diff(u(x,y),y)=0;
![]()
>
sol:=pdsolve(eq,u(x,y));
_F1 na solução a seguir é uma função arbitrária dos seus argumentos.
![]()
Para verificar a solução acima, usar subs():
simplify(subs(sol,lhs(eq)));
![]()
>
eq2:=diff(u(x,t),t$2)-diff(u(x,t),x$2)=0;
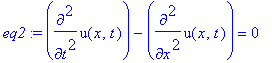
>
sol2:=pdsolve(eq2,u(x,t));
![]()
Para verificar a solução acima, usar subs():
simplify(subs(sol2,lhs(eq2)));
![]()
>
>
Solução de equações e inequaçõe s
Solução de equações
> eqn := x^3-1/2*a*x^2+13/3*x^2 = 13/6*a*x+10/3*x-5/3*a;
![]()
> solve( eqn, {x} );
![]()
Sistema de equações a seguir é linear
>
eqn1 := a+2*b+3*c+4*d+5*e=41;
eqn2 := 5*a+5*b+4*c+3*d+2*e=20;
eqn3 := 3*b+4*c-8*d+2*e=125;
eqn4 := a+b+c+d+e=9;
eqn5 := 8*a+4*c+3*d+2*e=11;
![]()
![]()
![]()
![]()
![]()
> solve( {eqn1, eqn2, eqn3, eqn4, eqn5}, {a, b, c, d, e} );
![]()
Sustema a seguir não é linear
>
eqn1 := a^2+2*b+3*c+4*d+5*e=41;
eqn2 := 5*a^2+5*b+4*c+3*d+2*e=20;
eqn3 := 3*b^2+4*c-8*d+2*e=125;
eqn4 := a+b+c+d+e=9;
eqn5 := 8*a+4*c+3*d+2*e=11;
![]()
![]()
![]()
![]()
![]()
> solve( {eqn1, eqn2, eqn3, eqn4, eqn5}, {a, b, c, d, e} );
![]()
>
fsolve( {eqn1, eqn2, eqn3, eqn4, eqn5}, {a, b, c, d, e} );
# fsolve() para ponto flutuante
![]()
> solve( arccos(x) = arctan(x), {x} ); # trigonométrica
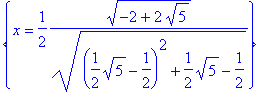
> eqn:=abs( (z+abs(z+2))^2-1 )^2 = 9; # exemplo contendo abs
![]()
> solve( eqn, {z});
![]()
Solução de inequações
> solve( {x^2<1, y^2<=1, x+y<1/2}, {x,y} );
![]()
>
ineq := x+y+4/(x+y) < 10:solve( ineq, {x} );
![]()
> expr := 2*sqrt(-1-I)*sqrt(-1+I); # exemplo contendo complexo (I é unidade imaginária)
![]()
> is( expr <> 0 );
![]()
>
Método SIMPLEX de otimização
> restart;
> with(simplex): # carrega package SIMPLEX de otimização
Warning, the protected names maximize and minimize have been redefined and unprotected
>
restrics:={14*x+y<=6,0<=x}; # restrições
obj:=y; # função OBJETIVO
pontomax:=maximize(obj,restrics);
![]()
![]()
![]()
> plot({-14*x+6,6},x=-1..1,thickness=3);
![[Maple Plot]](images/apost4145.gif)
> restrics:={15*x+y<=6,x+21*y<=4};
![]()
> obj:=3*x+4*y;
![]()
>
pontomax:=maximize(obj,restrics);
evalf(pontomax);
maximo:=eval(3*.3885+4*.1719);
![]()
![]()
![]()
>
plot3d({15*x+y-6,x+21*y-4,3*x+4*y},y=7/157..47/157, x=40/157..80/157,axes=boxed,thickness=3,
orientation=[-140,80],shading=ZHUE);
![[Maple Plot]](images/apost4151.gif)
>
plot3d({15*x+y-6,x+21*y-4,3*x+4*y},y=0.05..0.3, x=0.3..0.5,axes=boxed,
orientation=[120,70],shading=ZHUE,thickness=3);
![[Maple Plot]](images/apost4152.gif)
>
plot3d({3*x+4*y,1.85},x=0.3..0.4, y=0.05..0.45,axes=boxed,
shading=ZHUE,thickness=3);
![[Maple Plot]](images/apost4153.gif)
Exemplo de minimização
>
restrics := {14*x+3*y-3*z>=6,
3*x+8*z>=2,5*y-2*z<=1,
x<=2,2<=y,1<=z};
obj:=x+2*y+3*z;
pontomin:=minimize(obj,restrics);
![]()
![]()
![]()
> evalf(pontomin);
![]()
> evalf(27/28+2*2+3*9/2);
![]()
FINANCE package
> restart;with(finance);
![]()
![]()
Exercício 1:
Vamos supor que começando daqui a 30 dias, pelo testamento da Tia Maria, V vai receber $1 mil por mês durante 2 anos! Como V necessita hoje de uma quantia alta de uma só vez, V quer vender esta herança. Ou seja, V quer saber quanto isto valeria hoje, se a taxa de juros permanecer estável em p % ao ano. Ou seja, qual seria o valor presente do seu asset .
Primeiro calculamos a taxa mensal equivalente a p %.
>
# Vamos supor p= 0.07
taxames:=fsolve((1+x)^12=1+0.07, x, 0..0.01);
![]()
Note que o intervalo 0..0.01 é fornecido para selecionar a raiz correta
Agora aplicamos a função annuity()
> annuity(1000,taxames,24);
![]()
que é o valor presente desejado.
***********************************************************************
Exercício 2 - Black e Scholes
Uma outra surpresa da Tia Maria: ela lhe deixou uma opção de comprar 1 mil ações da empresa BigBluff por $80 cada, daqui a 6 meses! O valor atual destas ações é $101. Por quanto V poderia vender estas opções hoje? Para obter uma resposta V necessita conhecer uma certa medida estocástica de volatilidade destas ações. A sua corretora lhe diz que a tal medida é 0.28, baseada em dados históricos. Mais ainda, V conhece o modelo de Black e Scholes:
> evalf(blackscholes(101,80,0.07,6/12,0.28));
![]()
Este é o preço por ação da opção que V agradece muito à Tia Maria.
***********************************************************************
Exercício 3
Vamos supor que há um empréstimo de $1 mil com juro de 10 % por mês a ser amortizado com $500 ao final de cada mês. Os cálculos são feitos abaixo, e a tabela a seguir mostra os resultados.
> A:= amortization( 1000, 500, 0.10 );
![]()
![]()
Serão necessários 3 pagamentos: $500, $500, e $176. O custo do empréstimo é portanto $176.00.
> Tabela_Amort[n, Pagamento, Taxa-juro, Principal, Saldo] = matrix(A[1]);
![Tabela_Amort[n,Pagamento,Taxa-juro,Principal,Saldo]...](images/apost4166.gif)
A primeira coluna mostra o número do pagamento.
A segunda coluna mostra o pagamento mensal.
A terceira coluna mostra a alíquota do pagamento que contribui para pagar a parte dos juros.
A quarta coluna mostra o quanto do pagamento paga a parte principal.
A última coluna mostra o saldo em aberto.
***********************************************************************
Exercício 4
Vamos supor que desejamos calcular o valor presente de receitas variáveis, $200 daqui a 1 mês, $150 e $100 ao fim do mês 2 e 3, respectivamente.
A taxa de desconto é 3.8% por mês.
> cashflows( [200, 150, 100], 0.038 );
![]()
Genericamente, se a taxa de desconto for
![]() %, o valor presente das receitas é dada pela função cashflows:
%, o valor presente das receitas é dada pela função cashflows:
> cashflows( [200, 150, 100], r );
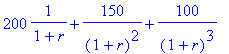
Geração de BlackScholes em C
>
### WARNING: persistent store makes one-argument readlib obsolete
restart;readlib(C):with(finance); # carregar as libraries
Error, could not find `C` in the library
![]()
![]()
> interface(verboseproc=3); # Isto é para ligar a opção "verbose"
> procgerado:=eval(blackscholes); # Isto é para armazenar o proc numa var.
![]()
>
### WARNING: calls to `C` for generating C code should be replaced by codegen[C]
C(procgerado); # Isto é para gerar em linguagem C
# a função procgerado() == blackscholes()
![]()
AVISO sobre erf(x)
erf(x) = 2/sqrt(Pi) * int(exp(-t^2), t=0..x)
A função blackscholes() na forma algébrica
> procgerado:=eval(blackscholes(A,E,R,N,Sd,H));
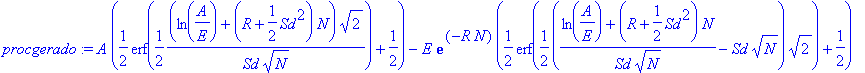
>
>
### WARNING: calls to `C` for generating C code should be replaced by codegen[C]
C(procgerado);
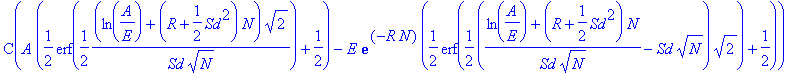
annuity()
Geração em C da função annuity() pode ser feita também da mesma forma
> procgerado:=eval(annuity);
![]()
![]()
>
### WARNING: calls to `C` for generating C code should be replaced by codegen[C]
C(procgerado);
![]()
futurevalue()
> procgerado:=eval(futurevalue);
![]()
>
### WARNING: calls to `C` for generating C code should be replaced by codegen[C]
C(procgerado);
![]()
presentvalue ()
>
fgerado:=eval(presentvalue(quantia,taxa,nperiodos));
# internamente este proc chama futurevalue()
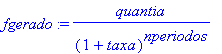
>
### WARNING: calls to `C` for generating C code should be replaced by codegen[C]
C(fgerado);
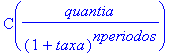
system() - system call em ms-windows
Para executar um comando de sistema, utilizar system();
> system(`dir/p`); # isto abre uma janela para mostrar o diretório
![]()
Da mesma forma system(`progr.exe`) provoca a execução do programa chamado progr em outra janela.