apost2a.html

Gravação e leitura de arquivos em disco e

geração de números com semente variável

Routo Terada

> restart;SAIDA:=fopen(sai,WRITE); primeiro, abrir arquivo sai para WRITE

> fprintf(SAIDA, `Este arquivo foi gravado para testar`);

^^^ note o acento grave aqui

^^^^ isto é só o comprimento da string acima

> fclose(SAIDA); fechar arquivo sai após gravar

conteúdo do arquivo sai é:

Este arquivo foi gravado para testar

Saída para arquivo em disco - gravação

> restart; SAIDA:= fopen(sai2, WRITE);

> x:= -123.456: printf(` x = %+08.2f \n`, x); total de 8 posições

x = -0123.46

> fprintf(SAIDA, ` x = %+08.2f \n`, x); destrói arquivo anterior!

> x:= 123.456: printf(` x= %f \n`, x);

x= 123.456000

> fprintf(SAIDA, ` x = %f \n`, x);

> str:= `marte e lua`: printf(` str= %s \n`, str);

str= marte e lua

> fprintf(SAIDA, ` str = %s \n`, str);

> fclose(SAIDA);

conteúdo do arquivo sai2 :

x = -0123.45
x = 123.456
str = marte e lua

Entrada de arquivo em disco - leitura

> restart;
Primeiro gravar arquivo cahamado entra1 que vai ser lido a seguir.

> SAIDA:= fopen(entra1, WRITE);
x:=12.3456: y:=78.9012: z:=45.67: t:=1.1:
fprintf(SAIDA, `%7.4f %7.4f \n %5.2f \n %3.1f`, x,y,z,t);
fclose(SAIDA);

conteúdo do arquivo entra1 em disco:

12.3456 78.9012
45.67
1.1

> ENTRA:= fopen(entra1, READ);
lis:=fscanf(ENTRA,`%f %f`); le uma lista de valores

> lis[1]+11;

> lista2:=fscanf(ENTRA,`%f`);

> fclose(ENTRA);

Geração de números aleatórios alterando _seed

> gera:=rand(1..52); gera um número entre 1 e 52

> gera(); gera(); cada chamada gera um outro número

> lis:=gera();

> for j in [1,2,3,4] do

> outro:=gera(); lis:=[outro,op(lis)]

> od;

> _seed:= 13; mudança da semente chamada _seed

> lis:=gera(); geração começa com nova semente

> for j in [1,2,3,4] do

> outro:=gera(); lis:=[outro,op(lis)]

> od;

> _seed:=1313: geração de float entre 0 e 1

> for j in [1,2,3,4,5] do

> printf(`\n %6.5f `,gera()/52.0);

> od;

.40385

.73077

.75000

.88462

.23077

Exercícios:

(1) Definir um valor arbitrário de _seed e depois gerar 6 números pseudo aleatórios usando gera().

(2) Alterar _seed para outro valor e gerar de novo 6 números; verificar que os números são diferentes.

GRÁFICOS

Gráficos 2D

> restart;plot([t,t^2,t=1.2..10.88],thickness=2);
# funcao parametrizada -
# lista com [eixo x, eixo y, variacao de t]

Exercício : traçar um gráfico de x ao cubo no intervalo de 1 a 12.

Mais de um gráfico

> restart;plot([x-x^3.3/2,sin(x)],x=0..1,linestyle=[2,3],
thickness=2,color=[red,blue]);

> plot([t,2*t*sin(t/4),t=0..8*Pi],thickness=2,color=brown);

> plot(x^2*exp(-x),x=0..10,thickness=2);

> plot([[5,5],[6.4,6.8],[7,8],[9,20]],thickness=2);

> plot(sin(x)/x,x=-2*Pi..2*Pi,thickness=2,
title=`Gráfico do Seno()`,labels=[`Tempo`,`Y `],axes=boxed);

Gráficos 3D

> plot3d(sin(4*x+y),x=-1..1,y=-1..1,axes=boxed,thickness=1);

> plot3d(-x^3+y^3,x=0..5,y=0..5,axes=boxed,
labels=[`Eixo x`,`tempo`,`Z `]);

Mais de um gráfico

> plot3d({sin(x*y), 2*x},
x=-2*Pi..2*Pi,y=-Pi..Pi,axes=boxed);

Quatro gráficos

> c1:= [cos(x)-2*cos(0.4*y),sin(x)-2*sin(0.4*y),y]:
c2:= [cos(x)+2*cos(0.4*y),sin(x)+2*sin(0.4*y),y]:
c3:= [cos(x)+2*sin(0.4*y),sin(x)-2*cos(0.4*y),y]:
c4:= [cos(x)-2*sin(0.4*y),sin(x)+2*cos(0.4*y),y]:
plot3d({c1,c2,c3,c4},x=0..2*Pi,y=0..10,
grid=[25,15],style=patch,axes=boxed);

Com variação de cor

> plot3d({c1,c2,c3,c4},x=0..2*Pi,y=0..10,grid=[25,15],
style=patch,color=sin(x),axes=boxed);

Exercício : Traçar um gráfico 3D de x*cos(x)+y*cos(y) para x e y no intervalo de -Pi a +Pi

MATRIZES E VETORES

> restart;
with(linalg); # carrega o pacote linalg com as
# funções listadas a seguir

Warning, the protected names norm and trace have been redefined and unprotected

Para criar uma matriz 4 por 2

> M := matrix(4,2,[12.2,15.5,-28.8,21.1,35.12,36.0,4.,4.9]);

> M2 := addcol(M,1,2,5);

Somar à coluna 2 da matriz M a coluna 1 multiplicada por 5

Somar à linha 4 de M2 a linha 2 multiplicada por 1/2

> M3 := addrow(M2,2,4,1/2);

Exercício:

Definir uma matriz A de 3 linhas e 4 colunas. Depois somar a linha 1 à linha 2 multiplicado por -1 .

col(mat,n) para extrair a enésima coluna da matriz mat.

row(mat,n) para extrair a enésima linha da matriz mat.

> A := matrix(4,4,[-14.4,15.63,1.0,19,21.23,23,26.27,-25.4,
-35.19,33,-31.5,38.8,48,40.13,47,41]);

> col(A,3); # extrai a coluna 3 da matriz A

> row(A,1);

Para calcular matriz adjunta

> adjoint(A); # calcula a matriz adjunta de A

Exercício : Calcular a matriz adjunta da matriz abaixo

> A := 'A': # apagar a definição anterior de A.
A := matrix(3,3,[-1.2,11,-12.3,22,-24,-2.2,31.3,-34,-32]);

> b := vector([4.222,-44.14,3.9]);

A seguir queremos resolver o sistema linear Ax=b pelo Algoritmo de Gauss-Jordan

Primeiro vamos concatenar as matrizes A e b.

> C := concat(A,b);

Agora aplicamos o Algoritmo de Gauss-Jordan para resolver o sistema linear

> solucao := gaussjord(C);

A seguir podemos extrair o vetor x, tal que Ax = b.

> x := col(solucao,4);

Podemos resolver o sistema usando linsolve(A,b) onde A e' uma matriz e b um vetor

> linsolve(A,b);

mulcol(mat,ncol,expr) para multiplicar a coluna ncol da matriz mat pela expressão expr.

mulrow(mat,nlin,expr) par multiplicar a linha nlin da matriz mat pela expressão expr.

> A := 'A':

> A := array([[-1.1,12.0,1.5,12.3],[21,-2.1,2.93,2.71],[-3.7,3.2,3.1,3.04],
[4.3,4.87,4.5,44.5]]);

> A1 := mulcol(A,3,1/5); # multiplica a coluna 3 de A por 1/5

> A2 := mulrow(A1,2,5); # multiplica a linha 2 de A por 5

Exercício : Resolver M x=b para a matriz M e vetor b abaixo

Multiplicação de matriz por escalar

scalarmul(mat,expr) para multiplicar ( por escalar ) cada elemento da matriz mat pela expressão expr.

> A3 := scalarmul(A2,x^2); # multiplica a matriz A2 por x^2

> AA := matrix(4,4,[]): # cria a matriz AA com elementos indefinidos

> for i from 1 to 4 do
for j from 1 to 4 do
AA[i,j] := subs(x=2, A3[i,j]):
od
od; # substitui x por 2 em todos os elementos da matriz A3 e
# atribui o resultado `a matriz AA

PRINT de matriz

> print(AA); # imprime a matriz AA

> map(diff,A3,x); # deriva A3 com relacao a x

Troca de linhas e colunas

swapcol(mat, i, j) troca as colunas i e j da matriz mat e mostra a matriz resultante.

swaprow(mat,i,j) troca as linhas i e j da matriz mat e mostra a matriz resultante.

> A4 := swaprow(A3,4,1); # troca as linhas 4 e 1 da matriz A3

> A5 := swapcol(A4,4,1); # troca as linhas 4 e 1 da matriz A4

Soma de matrizes

> A6 := matadd(A3,A5); # soma as matrizes A3 e A5

Exercício : Somar as duas matrizes abaixo com matadd()

Matriz bloco diagonal

> A := 'A':

> A := matrix(2,2,[1.21,1.5,-2.7,2.4]);

> B := 'B':

> B := matrix(3,3,[-1.29,1.3,-1.6,2.2,22.24,2.1,-3.4,-33,3.65]);

> BlockDiagonal(A,B); # constrói a matriz bloco diagonalizada
# formada por A e B.

Extensão de matriz

extend(mat, m, n, val) estende a matriz mat para uma matriz em que m linhas e n colunas

são acrescentadas a matriz mat. Às novas entradas na matriz mat são atribuidas o valor val.

> A := 'A':

> A := matrix(2,2,[1.95,11.2,-21,29]);

> B := 'B':

> B2 := extend(A,2,2,0); # acrescenta 2 linhas e 2 colunas à
# matriz A com valor 0

Exercício : Acrescentar a quarta linha com valor -1 à matriz

Cópia de matriz para uma outra matriz

> B1 := 'B1':

> B1 := copyinto(A,B2,3,3); # copia a matriz A em B a partir
# da posição (3,3);

Remoção de linhas e colunas

> B2 := 'B2':

> B2 := delcols(B1,1..2); # remove as colunas de 1 a 2 da matriz B1

> B3 := 'B3':

> B3 := delrows(B2,2..3); # remove as linhas de 2 a 3 da matriz B2

> B3 := copyinto(matrix(1,2,[12.2,11.7]),B3,1,1);
# copia a matriz 1 por 2, [12.2, 11.7],
# na matriz B3, a partir da posição (1,1)

Determinante e multiplicação de matrizes

> detB3 := det(B3); # calcula o determinante de B3

> B4 := evalm(B3^(-1)); # calcula a inversa de B3

> evalm(B3 &* B4); # verifica se o produto de B3 e B4 é
# a matriz identidade

Exercício : Calcular o determinante e a inversa da matriz

Matriz de Hilbert

> hilbert(5); # gera a matriz de Hilbert 5x5

Concatenação de matrizes

> A := 'A': B := 'B': C := 'C':

> A := matrix(2,2,[-11.3,-11,20,2.2]);

> B := matrix(2,2,[11.6,12.9,22,-2.92]);

> C := stackmatrix(A,B); # concatena as duas matrizes verticalmente

Matriz de Vandermonde e transposta de matriz

> A := 'A':

> A := vandermonde([-2,3.2,-2.3,4]);
# acha a matriz de Vandermonde associada à lista

> B := 'B':

> B := transpose(A); # calcula a transposta de A

Exercício : Calcular a transposta da matriz

Base de espaço vetorial

> A := 'A':

> A := matrix(5,5,[1,-2,2,1,-2,1,1,2,-2,-2,1,0,0,2,-1,0,0,0,-2,0,-2,1,0,1,2]);

> colspace(A); # acha uma base para o espaço coluna de A

> rowspace(A); # acha uma base para o espaço linha de A

Posto (rank) e núcleo (kernel) de matriz

> rank(A); # calcula o posto de A

> nullspace(A); # acha uma base para o espaço nulo de A.
# É o mesmo que kernel(A)

> kernel(A);

> A := 'A':

> A := matrix(3,4,[11.3,19.3,19.12,10,23.4,28.3,22.3,23,41,4.91,47.1,41.71]);

> rank(A); # acha o posto de A

Exercício : Calcular o posto e o núcleo da matriz abaixo

Algoritmo de Eliminação de Gauss

> gausselim(A); # aplica o método de eliminação de Gauss na matriz A

Exercício : Aplicar o Algoritmo de Eliminação de Gauss à matriz abaixo

Bases e transformação de uma base para outra

> B1 := 'B1': B2 := 'B2': # a seguir as colunas de B1 formam uma base
# para o espaço R^4. As colunas de B2
# formam outra base.

> B1 := matrix(4,4,[1,0,0,2,2,2,2,1,1,1,2,1,2,1,2,1]);

> B2 := matrix(4,4,[2,0,1,0,1,0,2,1,2,2,0,2,1,2,0,2]);

> v := vector([1,-1,5,-1]); # v é um vetor do R^4 com relação a base B1

A seguir, como encontrar v em relação à base B2, aplicando Gauss-Jordan

> B1_B2 := concat(B1,B2);

> r_B1_B2 := gaussjord(B1_B2); # aplica o método de Gauss-Jordan,
# assim obtemos a matriz de transformação
# da base B1 para B2

> trans := delcols(r_B1_B2,1..4); # elimina as colunas de 1 a 4
# para obter a matriz de transformação

Agora para achar v na base B2 basta multiplicar trans por v.

> v_B2 := evalm(trans &* v);

Algoritmo de GramSchmidt para obter base ortonormal

> v1:= 'v1': v2:= 'v2' : v3 := 'v3':

> v1 := vector([-2.89,-1,-2]):

> v2 := vector([0,-1.81,2]):

> v3 := vector([1,3,-2.44]):

Os vetores v1, v2 e v3 formam uma base para o espaço R^3.

Vamos aplicar o Algoritmo de GramSchmidt a este conjunto para obter uma base ortonormal.

> GramSchmidt([v1,v2,v3]);

Teorema de Laplace, cofator, determinante

> A := 'A':

> A := matrix(4,4,[12.2,10,-11,11.21,3,-1,-3,-1,-3,0,0,-1,2,-2,-3,1]);

> cof := (-1)^(2+3) * det(minor(A,2,3));
# calcula o cofator do elemento (2,3) da matriz A

> detLaplace := sum('(-1)^(1+i)*det(minor(A,1,i))*A[1,i]', 'i' = 1..4);
# Aplica o Teorema de Laplace para calcular o determinante de A

> detMaple := det(A); # calcula o determinante de A usando a função det()

Polinômio e matriz característica; autovetor e autovalor

> A := 'A': C := 'C':

> A := matrix(3,3,[14,-13.9,14.2,1,-3,1,-1,-1,-5]);

> C := charmat(A,lambda); # acha a matriz característica de A

> Eq := det(C) = 0; # acha o polinômio característico de A

> solve(Eq); # resolve a equação anterior para achar os autovalores de A

> eigenvals(A); # acha os autovalores de A

> eigenvects(A); # acha os autovetores associados a cada autovalor

Notação: [ ,1,{[ , , ]}] significa que

é o autovalor, 1 é a multiplicidade do autovalor e

[ ... ] são os autovetores associados a este autovalor.

Exercício : Calcular o polinômio característico e os autovalores da matriz abaixo

Forma Canônica de Jordan

> Digits:=20:
A := matrix(2,2,[1.1,1.2,22.3,0]);
jordA := jordan(A); # acha a forma canônica de Jordan da matriz A

Outra forma de calcular Jordan

> jordA := jordan(A,'T'); # acha a forma canonica de jordan da matriz A.
# 'T' é usado para retornar a matriz de
# transição tal que T^(-1)AT = jordA

> print(T); # imprime a matriz de transição

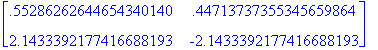
> B := evalm(inverse(T) &* A &* T); # calcula o produto T^(-1)AT

> equal( jordA, B); # verifica se as matrizes jordA e B são
# iguais (ou quase iguais)

Decomposição LU

> A := matrix([[1,-2,3],[2,k,6],[-1,3,k-3]]);

> Decomposto := LUdecomp(A,L='baixo',U='cima',
det='determ',rank='posto');

> posto;

> evalm(cima);

> evalm(baixo);

> map(normal,evalm(baixo &* cima));
# para verificar a decomposição

> determ;

Mesmo cálculo para k=3

> Decomp2:=LUdecomp(subs(k=3,op(A)),
L='baixo',U='cima',det='determ',rank='posto');

> determ;

Exercício : Calcular a decomposição LU da matriz abaixo

**************************************************************************

fopen()

**************************************************************************

Function: open - Opens a file for unbuffered reading or writing

Calling Sequence:
open(name, mode)

Parameters:
name - the name of the file to be opened
mode - one of READ or WRITE

Description:

opens the file with the specified name for unbuffered reading or writing as specified by mode and returns a file descriptor (a small integer).

RAW file I/O is always done with a file type of BINARY.

the special file names `default` and `terminal`, referring to the current and top-level input or output streams, cannot be used with open.

if the file is being opened for reading and does not exist, open generates an error.

if the file is being opened for writing and does not exist, it is created if possible, otherwise open generates an error.

if the file is already open, open generates an error.

if the limit for the maximum number of simultaneously open files has been reached, open generates an error. open`.

Examples:

> fd := open(testFile,WRITE);

> fprintf(fd,`This is a test\n`);

> close(fd);

**************************************************************************

fclose(),close

**************************************************************************

Function: fclose - Closes a buffered file

Function: close - Closes an unbuffered file or pipe

Function: process[pclose] - Closes a pipe to a process started with popen

Calling Sequence:
fclose(file ...)
close(file ...)
pclose(file ...)

Parameters:
file - one or more names or file descriptors of open files to be closed

Description:

Closes the specified file, which is assumed to have been opened either implicitly or by fopen, open, pipe, or popen.

fclose, close, and pclose do not return anything.

Closing a file ensures that all data is actually written to disk.

When exiting Maple by the quit, done, or stop command, all open files are automatically closed.

Closing a file which exists but is not open is harmless.

The functions close, fclose, and pclose are actually equivalent, and can be used interchangeably.

The pclose function is part of the process package, and so can be used in the form pclose(..) only after performing the command with(process) or with(process, pclose). The function can always be accessed in the long form process[pclose](..).

Examples:

> fd := fopen(testFile,WRITE,BINARY);

> fprintf(fd,`This is a test\n`);

> fclose(fd);

**************************************************************************

fprintf(),sprintf,printf

**************************************************************************

Function: fprintf - Prints expressions to file or pipe based on a format string

Function: sprintf - Prints expressions to a string based on a format string

Function: printf - Prints expressions to default stream based on a format string

Calling Sequence:
fprintf(file, fmt, x1, ..., xn);
sprintf(fmt, x1, ...,xn);
printf(fmt, x1, ...,xn);

Parameters:
file - a file descriptor or file name
fmt - the output format specification
x1, ..., xn - the expressions to be formatted

Description:

The fprintf function is based on a C standard library function of the same name. It uses the formatting specifications in the fmt string to format and write the expressions to the specified file.

The sprintf function is based on a C standard library function of the same name. It uses the formatting specifications in the fmt string to format and write the expressions into a Maple string, which is returned.

The printf function is based on a C standard library function of the same name. It uses the formatting specifications in the fmt string to format and display the expressions.

The call printf(...) is equivalent to fprintf(default,...).

The fprintf function returns a count of the number of characters written.

The format string, fmt, is a Maple string made up of a sequence of formatting specifications, possibly separated by other characters. Each formatting specification has the following format:
%[flags][width][.precision]code

The % symbol begins the format specification. One or more of the following flags can optionally follow the % symbol:
+
A signed numeric value is output with a leading + or - sign as
appropriate.
-
The output is left justified instead of right justified.
blank
A signed numeric value is output with either a leading - or a
leading blank, depending on whether the value is negative or
non-negative.
0
The output is padded on the left (between the sign and the first
digit) with zeroes. If - is also specified, 0 is ignored.

The optional width indicates the minimum number of characters to output for this field. If the formatted value has fewer characters, it is padded on the left (or right if - was specified) with blanks.

The optional precision specifies the number of digits that appear after the decimal point for floating point formats, or the maximum field width for string formats.

Both width and/or precision may be specified as *, in which case the width and/or precision are taken from the argument list. The width and/or precision arguments must appear, in that order, before the argument that is being output. A negative width argument is equivalent to the - flag having appeared.

The code indicates the type of object to be formatted. The code can be one of the following:
d
The object is formatted as a signed decimal integer.
o
The object is formatted as an unsigned octal (base 8) integer.
x or X
The object is formatted as an unsigned hexadecimal (base 16)
integer. The digits corresponding to the decimal numbers 10 through
15 are represented by the letters A through F if X is used, or a
through f if x is used.
e or E
The object is formatted as a floating point number in scientific
notation. One digit will appear before the decimal point, and the
number of digits specified by the precision will appear after the
decimal point (6 digits if no precision is specified). This is
followed by the letter e or E, and a signed integer specifying a
power of 10. The power of 10 will have a sign and at least 3 digits,
with leading zeroes added if necessary.
f
The object is formatted as a fixed point number. The number of digits
specified by the precision will appear after the decimal point.
g or G
The object is formatted using e (or E if G was specified), or f
format, depending on its value. If the formatted value would contain
no decimal point, d format is used. If the value is less than 10^(-4)
or greater than 10^precision, e (or E) format is used. Otherwise, f
format is used.
c
The object, which must be a Maple string containing exactly one
character, is output as a single character.
s
The object, which must be a Maple string, is output as a string of at
least width characters (if specified) and at most precision
characters (if specified).
a
The object, which can be any Maple object, is output in correct Maple
syntax. At least width characters are output (if specified), and at
most precision characters are output (if specified).
NOTE: truncating a Maple expression by specifying a precision can
result in an incomplete or incorrect Maple expression in the output.
m
The object, which can be any Maple object, is output in Maple's ".m"
file format. At least width characters are output (if specified), and
at most precision characters are output (if specified).
NOTE: truncating a Maple ".m" format expression by specifying a
precision can result in an incomplete or incorrect Maple expression
in the output.
M or N
The object, which can be any Maple object, is output in OpenMath
syntax. At least width characters are output (if specified), and at
most precision characters are output (if specified).
NOTE: truncating an OpenMath expression by specifying a precision can
result in an incomplete or incorrect Maple expression in the output.
ALSO NOTE: The outut uses OpenMath syntax, but assumes Maple
semantics; only Maple will be able to process the result. To produce
an OpenMath compliant result, additional preprocessing is required.
If the "%N" format was specified, no back-references will appear in
the output.
%
A percent symbol is output verbatim.

Characters in fmt but not within a format specification are output verbatim.

Because Maple allows one to freely convert between types, several of the format specifications will work with objects of types other than the ones they would be restricted to in a C program. Any of the floating point formats can accept integer, rational, or floating point objects; the object will be converted to a floating point value and output appropriately.

The printf functions will NOT automatically start a new line at the end of the output. If a new line is required, the fmt string must contain a newline character (`\n`). Also, output from the printf functions is NOT subject to line wrapping at interface(screenwidth) characters.

The %o, %x, and %X formats use the underlying implementation provided by the hardware vendor. As a result output of octal and hexadecimal values is subject to the restrictions of the machine architecture.

If the file being written to by fprintf is a STREAM or RAW file, and it is currently open in READ mode, it will be reopened in WRITE mode with type TEXT at the same offset.

If a file name is given to fprintf, and that file is not yet open, it is opened in WRITE mode with type TEXT.

Examples:

> printf(`%g %g %g\n`,123,123/456,123456789);

123 .269737 1.234568e+08

> printf(`%-2.5s:%2.5s:%2.5s\n`,M,Map,MapleV);

M :Map:Maple

> x := 23; y := -1/x;

> printf(`x=%+06.2f y=%+0*.*f y=%a y=%m y=%M\n`,x,6,2,y,y,y,y);

x=+23.00 y=-00.04 y=-1/23 y=#!"""#B y=

Error, (in fprintf) integer, string, or function call expected

> ### WARNING: sprintf now outputs strings; nprintf can be used if names are wanted
### WARNING: %x or %X format should be %y or %Y if used with floating point arguments
printf(`%a\n`,sprintf(`%o %x\n\n`,17129,17129));

Error, (in sprintf) integer, string, or function call expected

> ### WARNING: sprintf now outputs strings; nprintf can be used if names are wanted
str := sprintf(`x = %d, y = %g`,x,y);

Error, (in sprintf) integer, string, or function call expected

> length(str);

**************************************************************************

fscanf(),sscanf(),scanf

**************************************************************************

Function: fscanf - Parses expressions from a file or pipe based on a format string

Function: sscanf - Parses expressions from a string based on a format string

Function: scanf - Parses expressions from default input stream based on a format string

Calling Sequence:
fscanf(file, fmt)
sscanf(str, fmt)
scanf(fmt)

Parameters:
file - a file descriptor or file name
str - the string being scanned
fmt - the scanning format specification

Description:

The function fscanf is based on a C standard library function of the same name. It reads characters from a file, matching numbers and substrings according to a specification in fmt. Unlike the C fscanf, the Maple version returns a list of the scanned objects.

The function sscanf is based on a C standard library function of the same name. It scans through str, matching numbers and substrings according to a specification in fmt. Unlike the C sscanf, the Maple version returns a list of the scanned objects.

The function scanf is based on a C standard library function of the same name. It reads characters from the current input stream, matching numbers and substrings according to a specification in fmt. Unlike the C scanf, the Maple version returns a list of the scanned objects.

The call scanf(fmt) is equivalent to fscanf(default,fmt).

Each of the functions fscanf, sscanf, and scanf return a list of the scanned objects.

If no objects were scanned successfully, an empty list is returned.

If no objects were scanned successfully because the end of the input was encountered immediately, 0 is returned.

The format string, fmt, is a Maple string made up of a sequence of conversion specifications, possibly separated by other characters. Each conversion specification has the following format:
%[*][width]code

The % symbol begins the conversion specification. The optional * indicates that the object is to be scanned, but not returned as part of the result (i.e. it is discarded).

The width indicates the maximum number of characters to scan for this object. This can be used to scan one larger object as two smaller objects.

The code indicates the type of object to be scanned. It determines the type of object that will be returned in the resulting list. The code can be one of the following:
d or D
The next non-blank characters in the input must make up a signed
or unsigned decimal integer. A Maple integer is returned.
o or O
The next non-blank characters in the input must make up an
unsigned octal (base 8) integer. The integer is converted to
decimal and returned as a Maple integer.
x or X
The next non-blank characters in the input must make up an
unsigned hexadecimal (base 16) integer. The digits
corresponding to the decimal numbers 10 through 15 are
represented by the letters A through F (either capital or
lowercase) in the input. The integer is converted to decimal
and returned as a Maple integer.
e, f, or g
The next non-blank characters in the input must make up a signed
or unsigned decimal number, possibly including a decimal point,
and possibly followed by E or e, an optional sign, and a decimal
integer indicating a power of ten. The number is returned as a
Maple floating-point value.
s
The next non-blank characters, up to but not including the
following blank characters (or the end of the string) are
returned as a Maple string.
a
The next non-blank characters, up to but not including the
following blank characters (or the end of the string) are
collected and passed to the Maple parser. An unevaluated Maple
expression is returned.
m
A single Maple expression, encoded in Maple's ".m" file format
is collected from the input. Characters are read until a
complete expression is parsed; the width specification is
ignored.
M
A single OpenMath expression is collected from the input.
Characters are read until a complete expression is parsed; the
width specification is ignored.
c
The next character (blank or otherwise) is returned as a Maple
string. If a width is specified, that many characters (blank or
otherwise) are returned as a single Maple string.
[...]
The characters between [ and ] are taken as a list of characters
that are acceptable as a character string. Characters are
scanned from the input until one is encountered that is NOT in
the list. The scanned characters are then returned as a Maple
string.
If the list begins with a ^ character, the list is considered to
consist of all those characters NOT in the list.
If a ] is to appear in the list, it must immediately follow the
opening [ or the ^ if there is one.
A `-' can be used in the list to represent a range of
characters. For example, A-Z represents any capital letter. If
a - is to appear as a character instead of representing a range,
it must appear either at the beginning or the end of the list.
n
The total number of characters scanned up to the %n is returned
as a Maple integer.

non-blank characters in fmt but not within a conversion specification are skipped (but they must match the corresponding characters in the input). White space in fmt is ignored, except that a space immediately preceding a %c specification causes the %c specification to skip any blanks in the input.

The scanf functions use the underlying implementation provided by the hardware vendor for the %o and %x formats. As a result input of octal and hexadecimal integers is subject to the restrictions of the machine architecture.

with fscanf, if a file name is given, and that file is not yet open, it is opened in READ mode with type TEXT.

scanf will read entire lines from the default input stream, but only use up as many characters as are needed to satisfy the format specifications. The remaining characters will be saved for subsequent calls to scanf.

Examples:

The result will be a list containing a floating-point value, two integers, a string, and another integer.

> ### WARNING: sscanf now returns a string for the %s format instead of a name
sscanf(`123.456E7 123.456E7`,`%g%d.%d %[Ee] %d`);

The result will contain two strings and a floating-point value.

> ### WARNING: sscanf now returns a string for the %s format instead of a name
sscanf(`123.456E7 123.456E7`,`%s %c%f`);

The result will contain three floating-point values.

> ### WARNING: sscanf now returns a string for the %s format instead of a name
sscanf(`X=123.4 Y=-27.9 Z=2.3E-5`,`X=%f Y=%f Z=%f`);

> ### WARNING: sscanf now returns a string for the %s format instead of a name
sscanf(`25 1/(x^4+1) test`,`%d%a%s`);

**************************************************************************

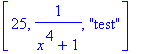
plot()

**************************************************************************

Function: plot - create a 2-dimensional plot of functions

Calling Sequence:
plot(f, h, v)
plot(f, h, v,...)

Parameters:
f - function(s) to be plotted
h - horizontal range
v - vertical range (optional)

Description:

A typical call to the plot function is plot(f(x),x=a..b), where f is a real function in x and a..b specifies the horizontal real range on which f is plotted.

Parametric plots are specified in the form [fx,fy,range]. The presence of a range in the third position of the list distinguishes parametric plots from multiple function plots.

Multiple functions can be plotted by placing a set or list of functions in the first argument. Options such as colour, thickness and style can be specified for each function by placing a list in the appropriate option argument (see below).

The plot function provides support for two-dimensional plots of one or more functions specified as expressions, procedures, or parametric functions. (When plotting a procedure, operator notation must be used.) See plot[function] for more information on plotting functions. For three-dimensional plots, see plot3d . A call to plot produces a PLOT data structure, which is then printed. For information on the PLOT data structure, see plot[structure] .

The horizontal and vertical range arguments h and v define the axis labels and the range over which the function(s) are displayed. They take one of the following forms: string, low..hi, or string=low..hi, where low and hi are real constants. See plot[range] for further information.

Remaining arguments are interpreted as options which are specified as equations of the form option = value. In particular, the style option allows one to plot the points as points only, or to interpolate them using line mode. See plot[options] for more information.

Setting the interface variable plotdevice (via the plotsetup command) to one of the values listed under plot[device] controls the type of plot which will be produced. See plot[device] and plot[setup] for information on how to set up plots on a particular device (printer or terminal).

Examples:

> restart;plot(cos(x) + sin(x), x=0..Pi);
plot(tan(x), x=-Pi..Pi);
plot([sin(t), cos(t), t=-Pi..Pi]);
plot(sin(t),t);

since no domain is specified in last example, we use t=-10..10
Same four plots, but as procedures or operators

> plot(cos + sin, 0..Pi);
plot(tan, -Pi..Pi);
plot([sin, cos, -Pi..Pi]);
plot(sin);

for expressions having discontinuities one can do

> restart;plot(tan(x),x=-2*Pi..2*Pi,y=-4..4, discont=true);
plot( -1 + 2*Heaviside(x-1) , x = -1..2, discont = true );

multiple plots (in a set or list)

> restart;plot([sin(x), x-x^3/6], x=0..2, color=[red,blue], style=[point,line]);

infinity plots

> restart;plot(sin(x), x=0..infinity);

point plots

> restart;l := [[ n, sin(n)] $n=1..10];
### WARNING: the definition of the type `symbol` has changed'; see help page for details
plot(l, x=0..15, style=point,symbol=circle);

some other plots

> s := t->100/(100+(t-Pi/2)^8): r := t -> s(t)*(2-sin(7*t)-cos(30*t)/2):
plot([r(t),t,t=-Pi/2..3/2*Pi],numpoints=2000,coords=polar,axes=none);
plot([x, tan(x), x=-Pi..Pi], -4..4, -5..5, tickmarks=[8,10]);

polar coordinates (with thickened curve)

> plot([sin(4*x),x,x=0..2*Pi],coords=polar,thickness=3);

**************************************************************************

plot3d()

**************************************************************************

Function: plot3d - three-dimensional plotting

Calling Sequence:
plot3d(expr1, x=a..b, y=c..d)
plot3d(f, a..b, c..d)
plot3d([exprf,exprg,exprh], s=a..b, t=c..d)
plot3d([f,g,h], a..b, c..d)

Parameters:
f,g,h - function(s) to be plotted
expr1 - expression in x and y.
exprf,exprg,exprh - expressions in s and t.
a,b - real constants.
c,d - real constants, procedures or expressions in x
x,y,s,t - names

Description:

The four different calling sequences to the plot3d function above all define surfaces. Facilities for plotting curves and other objects are in the plots package. The first two calling sequences describe surface plots in Cartesian co-ordinates while the second two describe parametric surface plots.

In the first call, plot3d(expr1,x=a..b,y=c..d), the expression expr1 must be a Maple expression in the names x and y. The range a..b must evaluate to real constants. The range c..d must either evaluate to real constants or be expressions in x. They specify the range over which expr1 which will be plotted. In the second call, plot3d(f,a..b,c..d), f must be a Maple procedure or operator which takes two arguments. Operator notation must be used, i.e. the procedure name is given without parameters specified, and the ranges must be given simply in the form a..b, rather than as an equation. The second range c..d can have arguments evaluating to real constants or procedures of one-variable.

A parametric surface can be defined by three expressions expr1, expr2, expr3 in two variables. In the third call, plot3d([ expr1,expr2,expr3 ],s=a..b,t=c..d), expr1, expr2, and expr3 must be Maple expressions in the names s and t. Finally, in the fourth call, plot3d([ f,g,h ],a..b,c..d), f, g and h must be Maple procedures or operators taking two arguments. Here again, operator notation must be used.

Any additional arguments are interpreted as options which are specified as equations of the form option = value. For example, the option grid = [m,n] where m and n are positive integers specifies that the plot is to be constructed on an m by n grid at equally spaced points in the ranges a..b and c..d respectively. By default a 25 by 25 grid is used, thus 625 points are generated. Other options include specification of alternate coordinate systems, rendering styles, etc. See the help page for plot3d[options] .

The result of a call to plot3d is a PLOT3D data structure containing enough information to render the plot. The user may assign a PLOT3D value to a variable, save it in a file, then read it back in for redisplay. See the help page for plot3d[structure] .

Note: for other types of 3d plots, see plots .

Examples:

> restart;plot3d(sin(x+y),x=-1..1,y=-1..1);
plot3d(binomial,0..5,0..5,grid=[10,10]);

can have alternate coordinate systems

> restart;plot3d((1.3)^x * sin(y),x=-1..2*Pi,y=0..Pi,coords=spherical,style=patch);
plot3d([1,x,y],x=0..2*Pi,y=0..2*Pi,coords=toroidal(10),scaling=constrained);
plot3d(sin(x*y),x=-Pi..Pi,y=-Pi..Pi,style=contour);

can have variable endpoints in some cases

> restart;plot3d(sin(x*y),x=-Pi..Pi,y=-x..x);
p:= proc(x,y) if x^2 < y then cos(x*y) else x*sin(x*y) fi end:
h:= proc(x) x^2 end:
plot3d(p,-2..2,-1..h);
plot3d([x*sin(x)*cos(y),x*cos(x)*cos(y),x*sin(y)],x=0..2*Pi,y=0..Pi);
plot3d(x*exp(-x^2-y^2),x=-2..2,y=-2..2,grid=[49,49]);

can specify a color function (or procedure)

> plot3d(x*exp(-x^2-y^2),x=-2..2,y=-2..2,color=x);
plot3d(p,-2..2,-1..h,color=h);

multiple 3d plots can also be done

> plot3d({sin(x*y), x + 2*y},x=-Pi..Pi,y=-Pi..Pi);
c1:= [cos(x)-2*cos(0.4*y),sin(x)-2*sin(0.4*y),y]:
c2:= [cos(x)+2*cos(0.4*y),sin(x)+2*sin(0.4*y),y]:
c3:= [cos(x)+2*sin(0.4*y),sin(x)-2*cos(0.4*y),y]:
c4:= [cos(x)-2*sin(0.4*y),sin(x)+2*cos(0.4*y),y]:
plot3d({c1,c2,c3,c4},x=0..2*Pi,y=0..10,grid=[25,15],style=patch);
plot3d({c1,c2,c3,c4},x=0..2*Pi,y=0..10,grid=[25,15],style=patch,color=sin(x));

**************************************************************************

linsolve

**************************************************************************

Function: linalg[linsolve] - solution of linear equations

Calling Sequence:
linsolve(A, b, 'r', v)
linsolve(A, B, 'r', v)

Parameters:
A - a matrix
b - a vector
B - a matrix
r - (optional) a name
v - (optional) a name

Description:

The function linsolve(A, b) finds the vector x which satisfies the matrix equation A x = b. If A has n rows and m columns, then vectdim(b) must be n and vectdim(x) will be m, if a solution exists.

If A x = b has no solution, then the null sequence NULL is returned. If A x = b has many solutions, then the result will use global names (see below) to describe the family of solutions parametrically.

The call linsolve(A, B) finds the matrix X which solves the matrix equation A X = B where each column of X satisfies A col(X,i) = col(B,i) . If A X = B has does not have a unique solution, then NULL is returned.

The optional third argument is a name which will be assigned the rank of A.

The optional fourth argument allows you to specify the seed for the global names used as parameters in a parametric solution. If there is no fourth argument, the default, then the global names _t[1], _t[2], _t[3], ... will be used in the vector case, _t[1][1], _t[1][2], _t[2][1], ... in the matrix case (where _t[1][i] is used for the first column, _t[2][i] for the second, etc). This is particularly useful when programming with linsolve. If you declare v as a local variable and then call linsolve with fourth argument v, the resulting parameters (v[1], v[2], ...) will be local to the procedure.

The command with(linalg,linsolve) allows the use of the abbreviated form of this command.

Examples:

> with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

> A := matrix( [[1,2],[1,3]] ):
b := vector( [1,-2]):
linsolve(A, b);

> B := matrix( [[1,1],[-2,1]] ):
linsolve(A, B);

> A := matrix( [[5,7],[0,0]] ):
b := vector( [3,0] ):
linsolve(A, b, 'r');

> r;

> linsolve(A, b, 'r', v);

> A := matrix([[5,7],[10,14]]);

> B := matrix([[3,0],[6,0]]);

> linsolve(A, B);

**************************************************************************

rand()

**************************************************************************

Function: rand - Random Number Generator

Calling Sequence:
rand()
rand(r)

Parameters:
r - (optional) an integer range or an integer

Description:

With no arguments, the call rand() returns a 12 digit non-negative random integer.

With an integer range as an argument, the call rand(a..b) returns a procedure which, when called, generates random integers in the range a..b.

With a single integer as an argument, the call rand(n) is the abbreviated form of rand(0..n-1).

More than one random number generator may be used at the same time, because rand(a..b) returns a Maple procedure, However, since all random number generators use the same underlying random number sequence, calls to one random number generator will affect the random numbers returned from another.

The global variable _seed can be used to alter the sequence of random numbers generated, by setting it to any positive integer. The function randomize() can also be used to modify the seed.

Examples:

> rand();

> die := rand(1..6):
die();

> die();

**************************************************************************

solve()

**************************************************************************

Function: solve - Solve Equations

Calling Sequence:
solve(eqn, var)
solve(eqns, vars)

Parameters:
eqn - an equation or inequality
eqns - a set of equations or inequalities
var - (optional) a name (unknown to solve for)
vars - (optional) a set of names (unknowns to solve for)

Description:

The solution to a single equation eqn solved for a single unknown var is returned as an expression. To solve a system of equations for some unknowns the system is specified as a set of equations eqns and a set of unknowns vars. The solutions for vars are returned as a set of equations.
The output from solve in general is a sequence of solutions. In the case of multiple solutions, you should put the solutions in a list or set before manipulating them further. When solve is unable to find any solutions, the empty sequence NULL is returned. This means that either there are no solutions, or simply that solve was unable to find the solutions. If solve was unable to find some solutions, it will set the global variable _SolutionsMayBeLost to true.
Two shortcuts for the input of equations and unknowns are provided. Wherever an equation is expected, if an expression expr is specified then the equation expr = 0 is understood. If vars is not specified, Maple will solve for all the variables that appear in eqns, i.e. indets(eqns,name) is used in place of vars.
In general, explicit solutions in terms of radicals for polynomial equations of degree greater than 4 do not exist. In these cases, implicit solutions are given in terms of RootOfs. Note that explicit solutions for the general quartic polynomial equation are not by default given because they are too complicated and messy to be of use. By setting the global variable _EnvExplicit to true then solve will return explicit solutions for quartic polynomials in all cases. By setting _EnvExplicit to false, all solutions which are not rational will be reported as RootOfs.
The number of solutions found can be controlled by changing the value of the global variable _MaxSols. If an integer is assigned to _MaxSols, only those many solutions will be computed and returned. The variable _EnvAllSolutions, if set to true, will force all inverse transcendental functions to return the entire set of solutions. This usually requires additional, system created, variables, which take integer values. Normally such variables are named with prefix _Z for integer values, _NN for non-negative integer values and _B for binary values (0 and 1).
When abs is used in the context of solve, solve assumes that the argument to abs is real-valued.
For solving differential equations, use dsolve. For purely floating-point solutions use fsolve. Use isolve to solve for integer solutions, msolve to solve modulo a prime; rsolve for recurrences, and linalg[linsolve] to solve matrix equations.
Further information is available for the subtopics solve[subtopic] where subtopic is one of