Antes de sua aula síncrona desta semana, estude os conteúdos abaixo e os materiais recomendados e tente resolver os exercícios. Os assuntos e exercícios serão discutidos pelo(a) professor(a) na aula.
Uma função é uma unidade de código de programa autônoma desenhada para cumprir uma tarefa particular.
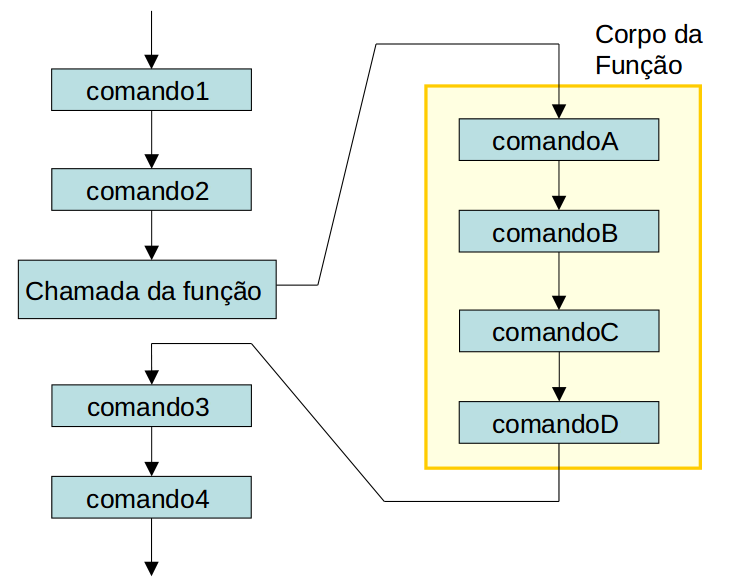
A chamada de uma função desvia a execução do código para o corpo da função (bloco de código da função):

fatorial(n) que
recebe um inteiro n e devolve o fatorial de n.n e k e calcula o
coeficiente binomial, do número n,
na classe k, isto é,
o número de combinações de n
termos, k a k, dado por n!/(k!(n-k)!).
Escreva essa função usando a função
fatorial(n) do item anterior.n, com n > 0, e que imprime o Triângulo de Pascal com n linhas.
Exemplo: para n = 5, o programa deve escrever:
1 1 11 2 1 1 3 3 1 1 4 6 4 1
def fatorial(n):
fat = 1
i = 2
while i <= n:
fat *= i
i += 1
return fat
def binomial(n,k):
return fatorial(n)//(fatorial(k)*fatorial(n-k))
def main():
print("Triângulo de Pascal")
n = int(input("Digite o número de linhas: "))
i = 0
while i < n:
j = 0
while j <= i:
b = binomial(i,j)
print("%3d "%b,end="")
j+= 1
print()
i += 1
main()
Faça um programa que lê um número inteiro n,
com n > 0, e para cada número entre 1 e n indica
se ele é soma de dois primos.
Por exemplo, para n = 8 o programa deve escrever
1 não é soma de primos2 não é soma de primos3 não é soma de primos4 é soma dos primos 2 e 25 é soma dos primos 2 e 36 é soma dos primos 3 e 37 é soma dos primos 2 e 58 é soma dos primos 3 e 5
def primo(n):
div = 2
ehprimo = True
while div < n:
if n % div == 0:
ehprimo = False
div += 1
if n <= 1:
ehprimo = False
return ehprimo
def main():
n = int(input("Digite n: "))
i = 1
while i <= n:
encontrou = False
j = 2
while j < i and not encontrou:
if primo(j) and primo(i-j):
encontrou = True
p1 = j
p2 = i-j
j += 1
if encontrou:
print("%d é soma dos primos %d e %d"%(i,p1,p2))
else:
print("%d não é soma de primos"%i)
i += 1
main()
Em Python, existem várias funções matemáticas prontas do
módulo math. Um exemplo de função desse módulo é a
factorial, que calcula o fatorial de um número.
Para usar uma função do módulo math, devemos primeiramente
importar o módulo no código, usando o comando import math, e
depois chamar a função. O exemplo abaixo mostra uma chamada à
função factorial.
import math
n = int(input("Digite o valor de n: "))
fat = math.factorial(n)
print("Fatorial de",n,"é",fat)
math.sqrt(x) do
módulo de matemática da linguagem Python
(import math), escreva uma função que
recebe as coordenadas cartesianas de dois pontos no plano e
devolve a distância entre os pontos.(x0, y0) e uma sequência de n > 1
pontos e determina o ponto mais próximo do ponto origem.
import math
def distancia(x1,y1,x2,y2):
return math.sqrt((x2-x1)**2 + (y2-y1)**2)
def main():
print("Digite as coordenadas do ponto de origem", end="")
x0 = float(input("x: "))
y0 = float(input("y: "))
n = int(input("Digite a quantidade de pontos: "))
print("Digite as coordenadas de um novo ponto", end="")
x_menor = float(input("x: "))
y_menor = float(input("y: "))
menor_distancia = distancia(x_menor,y_menor,x0,y0)
while n>1:
print("Digite as coordenadas de um novo ponto", end="")
x = float(input("x: "))
y = float(input("y: "))
d = distancia(x,y,x0,y0)
if d < menor_distancia:
x_menor = x
y_menor = y
menor_distancia = d
n -= 1
print("O ponto mais próximo de (%.2f,%.2f) é (%.2f,%.2f)" %(x0,y0,x_menor,y_menor))
main()
O MDC de dois números inteiros é o maior número inteiro que divide ambos sem deixar resto.
Exemplos:Algoritmo de Euclides: Para dois números A e B:
def MDC(a, b):
if a < b:
a,b = b,a
while b > 0:
r = a % b
a = b
b = r
return a
def main():
print("MDC entre a e b:")
a = int(input("Digite a: "))
b = int(input("Digite b: "))
print("MDC =", MDC(a,b))
main()
Dados um número inteiro n>0 e uma sequência com n números inteiros maiores do que zero, determinar o máximo divisor comum entre eles. Por exemplo, para a entrada
3 42 30 105
o seu programa deve escrever o
número 3.
DICA: O MDC é uma operação associativa.
Exemplo: MDC(A,B,C,D) = MDC(MDC(A,B),C,D) = MDC(MDC(MDC(A,B),C),D)
def MDC(a, b):
if a < b:
a,b = b,a
while b > 0:
r = a % b
a = b
b = r
return a
def main():
n = int(input("Digite n: "))
mdc = int(input("Digite o primeiro número: "))
i = 1
while i < n:
num = int(input("Digite o próximo número: "))
a = mdc
b = num
mdc = MDC(a, b)
i += 1
print("MDC =",mdc)
main()