sobre Pensamento Computacional para professores de Matemática
No noticiário #75 da Sociedade Brasileira de Matemática publiquei uma coluna sobre pensamento computacional. No texto, uso um exemplo para discutir diferentes atividades e como elas se alinham à visão ali apresentada.
Como o espaço da coluna é limitado, trago nesta página um detalhamento um pouco maior dos exemplos
atividades exemplares
O exemplo mencionado no texto deriva da habilidade EF06MA04 da BNCC, que pede o uso de fluxograma para representar a resolução de um problema simples e sugere, como exemplo, o problema de determinar a paridade de um número natural
Não pretendo alongar a discussão que apresentei no texto, pois a ideia que pretendia defender esta posta nele próprio, apenas disponibilizar mais detalhes sobre os exemplos que comentei ali.
A primeira atividade que coloquei no texto foi: escrever como determinar se um número é divisível por 2 na forma de um fluxograma.
Usualmente, esse processo é descrito como: um número natural é par se o seu algarismo das unidades é par.
Note que a descrição é muito simples e clara, não demandando por si só um outro tipo de representação nem mesmo a sua automatização, pois não se trata de um processo lento.
Se quisermos representá-lo na forma de um fluxograma, temos algumas possibilidades e abaixo trago algumas delas. Um dos problemas que aponto no texto é que essa nova forma de representar não melhora o entendimento do processo e eu diria que até pode atrapalhar, já que a leitura de um fluxograma demanda familiaridade com seus elementos.
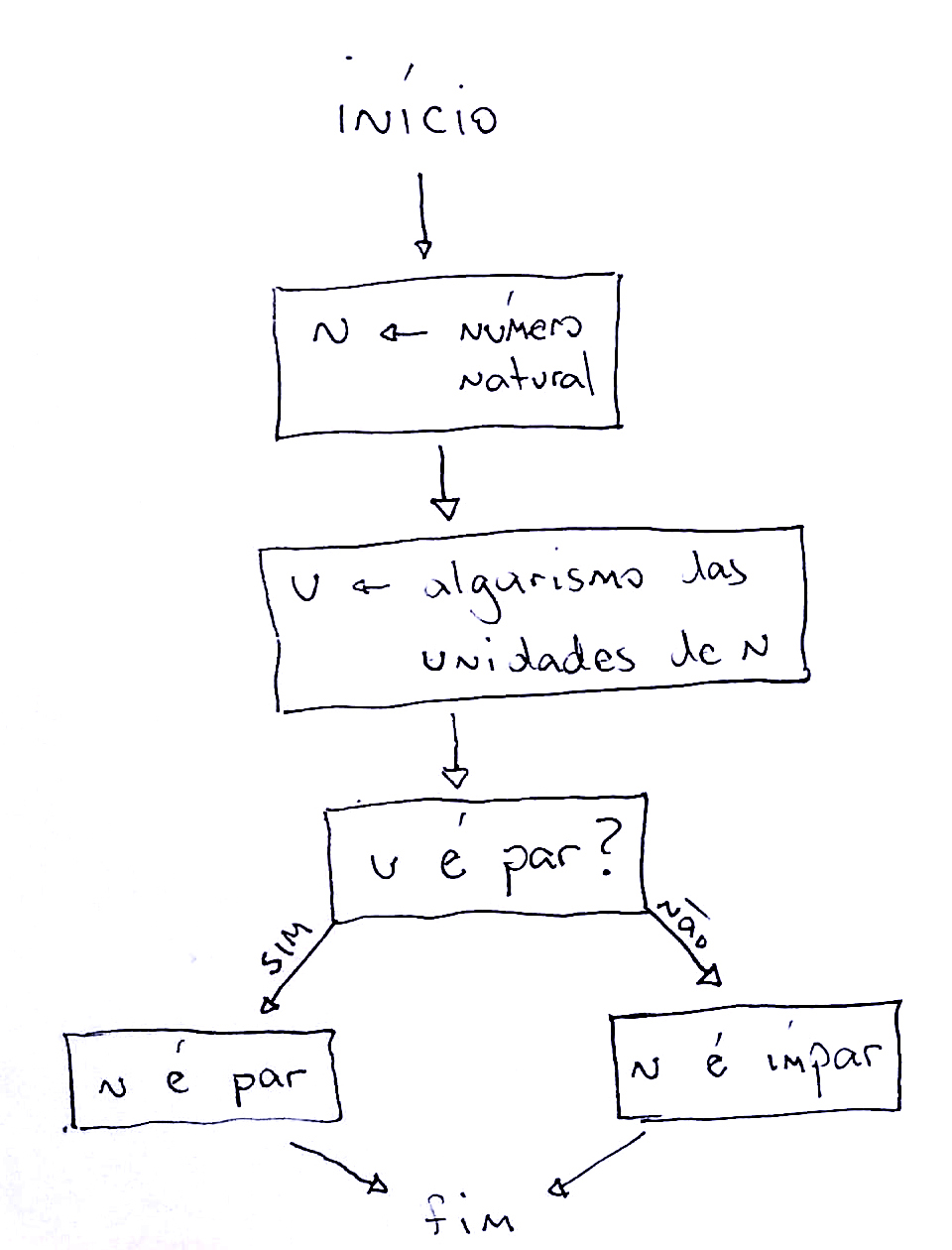
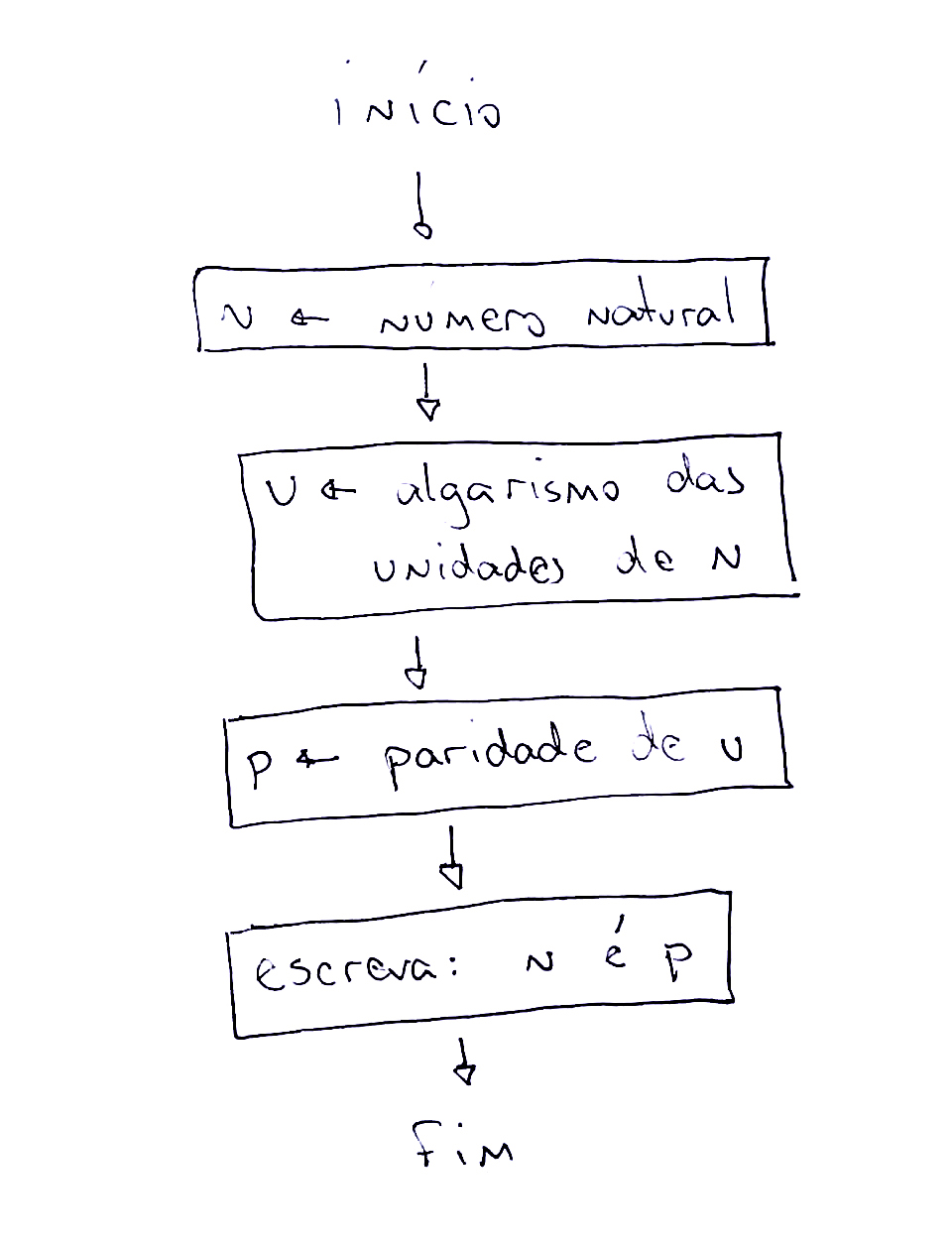
Se tentarmos escrever um algoritmo para determinar a paridade de um número natural em alguma linguagem de programação, notaremos mais um problema: a implementação do critério de divisibilidade retratado nos fluxogramas acima é mais difícil do que a realização da divisão inteira do número dado por 2, que é o que se pretende evitar ao ensinar critérios de divisibilidade. O fluxograma abaixo representa este método

Logo abaixo trago o mesmo método mostrado acima escrito em Python (agradecimentos ao projeto SageMathCell por viabilizar essa funcionalidade).
Veja que escrito dessa forma, o algoritmo não trata mais de critério de divisbilidade, porém, deixa evidente como generalizar o processo para quanlquer divisor, o que nos leva à segunda pergunta que coloquei no texto: como podemos usar uma linguagem de programação para determinar se um número dado é divisível por um outro número dado?
Essa nova pergunta sim é interessante para o desenvolvimento do pensamento computacional por viabilizar discussões que não seriam interessantes no lápis e papel (por serem muito trabalhosas) e por tornar viável a formulação de novas perguntas, como a terceira que coloquei no texto: como podemos identificar se um número dado é primo?
Essa pergunta é bastante ambiciosa do ponto de vista matemático, mas pede o uso de algum recurso computacional por exigir a realização de muitos passos repetitivos e propensos a erro humano. Um algoritmo bastante ingênuo que responde a essa pergunta é mostrado abaixo.
Mas veja que ele pode ser muito melhorado e a discussão dessas melhorias são muito ricas do ponto de vista computacional, afinal, em uma discussão como essa o algoritmo está sendo colocado como foco e eficiência de algoritmos é um tópico fundamental em computação. E mais ainda: a discussão é muito rica do ponto de vista matemático, pois:
- Uma primeira melhoria é perceber que podemos checar os divisores apenas até a raiz quadrada de n;
- O código pode ser interrompido quando o primeiro divisor é encontrado
- Não precisamos checar, como divisores, todos os números naturais menores ou iguais a raiz quadrada de n, mas apenas os números que são primos;
Veja que os argumentos acima são desenvolvidos a partir de conceitos matemáticos pertinentes ao tema que está sendo trabalhado.Podemos ir mais além, e promover outras habilidades do pensamento computacional, e também outros conceitos matemáticos, ao discutirmos como esse mesmo códgo poderia ser reaproveitado para obter outras propriedades numéricas, como:
- A decomposição de um número em fatores primos;
- Uma lista de número primos em um intervalo usando um processo equivalente ao crivo de Eratóstenes;
- O máximo divisor comum ou o mínimo múltiplo comum entre dois números dados.
Abaixo, mostro como ajustar o algoritmo acima para obter (de maneira ainda não otimizada) o máximo divisor comum entre dois números dados e convido o leitor a ajustá-lo para que obtenha o mínimo múltiplo comum.
Ainda que este exemplo ainda use conteúdos e conceitos bastante tradicionais do currículo de matemática, sem trazer novidades em termos dos tópicos abordados, ele (diferentemente do caso do fluxograma para identificar a paridade de um número) permite discussões relacionadas a: otimização do algoritmo, reutilização do algoritmo para solução de outros problemas relacionados e automatização de um processo que pode ser muito longo de feito manualmente. Essas possibilidades, no meu ponto de vista, são as que de fato promovem habilidades ligadas ao uso de computadores como ferramentas para resolver problemas.
encerramento
Espero que esta página tenha complementado o entendimento do texto publicado no noticiário da SBM e sirva de inspiração para colegas professores de matemática e formadores de professores. Se quiser uma leitura mais extensa e acadêmica sobre o tema, recomendo a seção 3.1 deste artigo.
Também sugiro o webnário que ofereci pela SBM em 2021 sobre o mesmo tema e o módulo sobre Pensamento Computacional que criei para o projeto Livro Aberto de Matemática, no qual abordo programação de computadores para professores de Matemática pensando em um curso de Matemática para o Ensino Médio.
Se estiver interessado em outras iniciativas relacionadas à Computação na Educação Básica, sugiro o preenchimento deste formulário para que eu possa entrar em contato com você periodicamente (não mais do que uma vez por bimestre) com recomendações de materiais, texto, cursos e oficinas.