Introdução à obtenção de zeros de funções
Nesta seção apresentaremos o método de Newton-Raphson para obtenção de "zeros" (ou raízes) de funções (contínuas e deriváveis).
A obtenção de "zeros de funções" tem muita aplicação prática, por exemplo, para a determinação de pontos ótimos (como pontos que minimizam determinada função objetivo). Outra aplicação interessante é possibilitar o cálculo de funções "complexas" (que não podem ser computadas apenas com somas e subtrações), como é o caso da função raíz quadrada.
1. Ideia do método
O objetivo é: dada uma função real f(.) (contínua e derivável), obter sua raíz x, ou seja, o ponto x para o qual f(x)=0.
A ideia do método é construir uma sequência de pontos que estejam cada vez mais próximos da raíz da função e para isso será usado um processo iterativo
baseado na contrução de retas tangentes a um ponto da curva (x,f(x)), como ilustrado na figura 1.
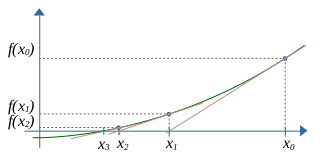
Fig. 1. Ilustração do processo iterativo de Newton-Raphson para obtenção de zero de função (com 3 passos).
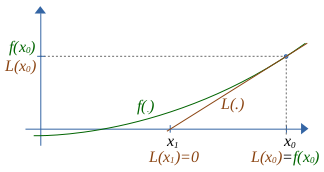
- Reta tangente. Dado um valor real xk, construir a reta Lk(.) tangente à curva definida por f(.) no ponto (xk,f(xk)),
ou seja, utilizando apóstrofe para indicar a derivada (f'(.)) devemos ter
Lk(xk)=f(xk) e L'k(x) =f'(x) (em x=xk) (1)
A imagem abaixo ilustra a reta L(.) tangente à curva definida pela função f(.), no ponto x0.
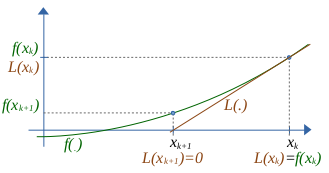
- Uma vez construída a reta Lk(.), a utilizaremos para obter o "zero" dessa reta: o ponto xk+1 para o qual Lk(xk+1)=0.
- Se a distância entre xk e xk+1 é suficientemente pequena (a definir), a resposta é o último ponto (xk+1);
senão, devemos repetir o processo para xk+1, ou seja, refazer o passo 1 dessa vez com xk+1.
O critério de parada no passo 3 é utilizado para detectar convergẽncia (de modo prático), porém a demonstração matemática de que a sequência efetivamente converge depende da função e do ponto inicial.
2. Construção da reta tangente
Toda reta L(x) é da forma L(x)=ax+b, sendo a o coeficiente angular e b o deslocamento.
No processo de Newton-Raphson, a cada passo interessa a reta que passa pelo ponto xk e cuja inclinação
coincida com a tangente de f(.) no ponto xk.
Desse modo, usando Cálculo I sabemos que a=f'(xk) (derivada no ponto) e, como a reta deve coincidir com a função no ponto
xk: L(xk)=f(xk), segue que f(xk)=f'(xk)*xk+b e
portanto b=f(xk)-f'(xk)*xk,
logo L(x) = f'(xk)*x + f(xk) - f'(xk)*xk, ou seja,
L(x) = f'(xk)*(x-xk)+f(xk) (2)
Note que, de fato, a reta L(.) assim definida tem as duas propriedades desejadas:
- Inclinação de L(.) coincide com inclinação de f(.) em xk (i.e. f'(xk)), pois: L'(x) = f'(xk) (em todo ponto x, em particular em x=xk);
- A reta passa por (xk,f(xk)), pois: L(xk) = f'(xk)*(xk-xk)+f(xk) = f(xk).
3. Obtendo novo ponto (mais próximo da raíz)
Toda reta a*x+b não paralela ao eixo x tem raíz, pode-se obtê-la isolando o valor de x para o qual a*x+b=0. No caso de interesse, devemos encontrar x para o qual L(x)=0, ou seja, 0 = f'(xk)*(x-xk)+f(xk) = f'(xk)*x-f'(xk)*xk+f(xk) e portanto x = (f'(xk)*xk - f(xk))/f'(xk) = xk - f(xk)/f'(xk), e desse modo o novo ponto xk+1 será
xk+1 = xk - f(xk)/f'(xk) (3)
A imagem abaixo ilustra o processo de obtenção do novo ponto xk+1 e como ele será usado para obter o seguinte, xk+2.
4. Método de Newton-Raphson (critério de parada)
Desse modo, dada uma função f(.) inicia-se o processo com x0 (por exemplo x0=0) e segue até que a diferrença entre dois pontos seja suficientemente pequena (e.g., menor que 0.0000000001).
1. Dado x0 (com f'(x0) não nulo)
2. Seja x1 := x0 - f(x0)/f'(x0)
3. Enquanto (distancia_entre(x0,x1) < Erro) // pode-se definir Erro:=0.0000000001
4. x0 := x1;
5. x1 := x0 - f(x0) / f'(x0)
Algoritmo 1. Esquema genérico do algoritmo Newton-Raphson.
Uma questão importante é saber sob quais condições o algoritmo acima converge, mas este é uma assunto para um curso de Cálculo.
Por outro lado, se a função for de classe C1 (derivada contínua) e
xk convergir para um
5. Método de Newton-Raphson aplicado à obtenção de raíz quadrada
Se o objetivo é obter a raíz quadrada de um valor real x, podemos transformar este problema em outro, para obtenção de zero de função e daí aplicar o método de Newton-Raphson.
Se f(x)=x1/2, podemos definir y := f(x), então y2 = x.
Assim podemos definir a função g(x)=y2-x e encontrar o "zero" para g(.) equivale a encontrar a raíz quadrada de x, pois
g(y)=0 ⟺ 0 = y2-x ⟺ y2 = x (4)
A função g(.) é um polinômio em y, sendo fácil obter sua derivada que é g'(y)=2y, desse modo o método de Newton-Raphson para g(.) fica:
xk+1 = xk - g(xk)/g'(xk) = xk - (xk2-x)/(2*xk) =
= xk - xk2/(2*xk) + x/(2*xk) =
xk - xk/2 + x/(2*xk) = xk/2 + x/(2*xk) = (1/2)(xk + x/xk)
ou seja, a sequência que (esperamos) aproxima a raíz de x é dada pela seguinte fórmula
xk+1 = (0.5)*(xk + x/xk) (5).
Exemplo. Vamos aplicar a iteração (5) para obter as raízes de 8 e de 16, ou seja, obter aproximações para 81/2 e 161/2.
| Iteração k | g(8)-81/2=0 | g(16)-161/2=0 |
| 1 | 4.500000 | 8.500000 |
| 2 | 3.138889 | 5.191176 |
| 3 | 2.843781 | 4.136665 |
| 4 | 2.828469 | 4.002258 |
| 5 | 2.828427 | 4.000001 |
| 6 | 2.828427 | 4.000000 |
| 7 | 2.828427 | 4.000000 |
Experimente implementar um algoritmo para gerar a sequência dada por (5), usando o esquema de algoritmo 1 acima.
Leônidas de Oliveira Brandão
http://line.ime.usp.br
Alterações:
2022/05/28: várias melhorias no texto, novas imagens;
2022/05/26: várias melhorias no texto, pequenas correções e troca da imagem "img_fx_xkmais1_02.png" pela "img_fx_xkmais1_03.png";
2022/05/25: primeira versão