Introdução aos números em ponto flutuantes
Nesta seção examinaremos resumidamente como o computador representa números reais. A seção seguinte foi redigida para aqueles que desejam conhecer mais, estudando-a pode-se compreender a matemática associada ao conteito de representação de números em um computador digital e a razão do termo ponto flutuante.
Normalmente deve-se utilizar um número fixo de bits para representar cada número. Por exemplo, se determinado computador usar apenas 2 bytes (ou 16 bits) para representar um real e convencionar-se que o primeiro byte armazena a parte inteira e o segundo byte a parte fracionária, teríamos uma variabilidade pequena de números. Como visto no texto introdutório sobre inteiros, com 8 bits, teríamos (simplificadamente) desde o 11111111 (primeiro bit indica negativo) até o 01111111, que em decimal corresponderia ao intervalo do -127 até o +127, pois
[ Ponto fixo | Ponto flutuante (PF) | PF super simplificado | Exemplo | Erros | Entrada/saída ]
Para apresentar o conceito que interessa, de ponto flutuante, apresentarei sua contra-parte, como seria uma representação em ponto fixo. Vamos continuar usando 2 bytes (logo 16 bits) e considerar 3 agrupamentos: P1. o primeiro bit para representar o sinal do número (s=0 para positivo e s=1 para negativo); P2. os próximos 7 como a parte "decimal" (após vírgula decimal); e P3. os últimos 8 bits para o valor inteiro do número.
Assim, para obter o maior valor positivo que poderia ser representado nesta notação, deveríamos deixar o primeiro bit em zero (para ser positivo) e todos os seguintes "ligados":
| Valor dos dígitos binários: |
| (deixei espaço em branco para indicar os 3 agrupamentos). | |||||
| Valor posicional dos dígitos: |
|
Assim, a parte "decimal" P2 (1111111) corresponde em decimal:
Portanto o maior positivo, convertendo para decimal, seria a soma de (1) e (2): 255.992188. Desse modo, em ponto fixo:
| - maior valor positivo em binário | 0 1111111 111111112 | = | 255.992188 em decimal; | |
| - menor valor estritamente positivo em binário | 0 0000001 000000002 | = | 0.007812 em decimal. |
Um modelo de representação para real mais eficiente: ponto flutuante
Uma alternativa mais eficiente e amplamente utilizada na prática é a representação em ponto flutuante. Nessa representação também quebramos o número em três agrupamentos, a primeira sendo o sinal s, a segunda o expoente e e a terceira sendo mantissa m, assim o valor do número seria s x m x be. Se a mantissa tiver p dígitos, o número é: s x d0d1...dp-1 x be.
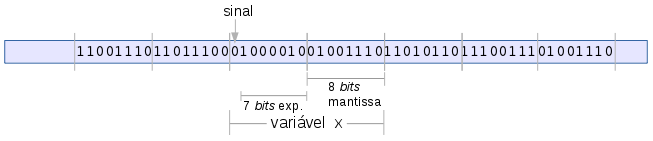
Fig. 1. Representação em memória para ponto fixo para representar reais, com 7 bits de expoente e 8 bits para mantissa.
Assim, nota-se que a diferença entre as representações em ponto flutuante e em ponto fixo é o tratamento do segundo agrupamento. Para poder comparar ambas as representações, vamos novamente supor um computador com reais usando apenas 2 bytes.
No segundo agrupamento, devemos ter expoenete negativo e expoenete positivo, novamente usamos o truque do primeiro bit "ligado" indicar potência negativa e 0 para potência positiva. Assim, a variação vai de 1111111 (correpondendo ao decimal -63) até 1111111 (correpondendo ao decimal +63).
De forma análoga, no terceiro agrupamento, para mantissa, as possibilidades de representação vão desde usar todos os bits "desligados" (00000000) até todos os bits "ligados" (11111111, que corresponde ao decimal 255).
Desse modo, o maior real positivo em ponto flutuante é obtido usando a maior potência e maior mantissa possiveis, respectivamente 0111111 e 11111111, que em decimal corresponderia aos valores 63 e 255, de acordo com (3) e (4) acima. Portanto, o maior real positivo em notação ponto flutuante é 255 x 263, um número gigantesco 255 x 263 = 2351959869397967831040.0 > 2.3 x 1021.
| Expoente: | 25 + 24 + 23 + 22 + 21 + 20 | = | 32 + 16 + 8 + 4 + 2 + 1 | = | 63 (3) |
| Mantissa: | 27 + 26 + 25 + 24 + 23 + 22 + 21 + 20 | = | 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 | = | 255 (4) |
De forma análoga, podemos computar o menor valor estritamente positivo que conseguimos com essa representação. Como são 7 bits para expoente e 8 bits para a mantissa, devemos pegar no agrupamento P2 a sequência 1111111 (maior potência negativa possível) e no agrupamento P3 o menor valor positivo, que seja maior que zero, portanto 00000001. Convertendo 1111111 para decimal, temos o valor -63, logo o menor positivo é: 2-63 que é aproximadamente 0.00000000000000000010842021724855044340074528008699 ~= 10-19 ("tremendamente" pequeno).
Portanto o maior e o menor valor positivo em notação ponto flutuante está indicado na tabela 2.
| - maior valor positivo em binário | 0 0111111 111111112 | > | 2.3 * 1021 em decimal; | |
| - menor valor estritamente positivo em binário | 0 1111111 000000012 | ~= | 10-19 em decimal. |
Comparando os resultados de ponto flutuante com ponto fixo, tabelas 1 e 2, percebemo que ponto flutuante produz resultados muito melhores em termos de capacidade de "simular" os números reais.
Representação em ponto flutuante
Esta técnica de representação é a mais utilizada nos computadores, ela utiliza um bit para sinal, uma quantidade pequena de bits para o expoente e uma quantidade maior de bits para a parte "principal" do número. Em um dos padrões de representação (IEEE 754) o número é representado com 11 bits para o expoente e 52 bits para a mantissa.
Exemplo de representação em ponto flutuante
Para ilustrar o funcionamento de ponto flutuante, suponha um computador que use representação em decimal (os computadores na verdade usam base binária), tendo apenas 3 dígitos para mantissa e o expoente sendo de -4 até 4, assim teríamos p=3 e -4<e<4.
Deste modo, o maior valor real que pode ser representado seria o 999000, pois tomando a maior mantissa e maior expoente, teríamos 103 x 999 = 999000.
Já o menor valor estritamente positivo que conseguiríamos seria o 0.001, pois tomando a menor mantissa positiva e menor expoente possível (-3), teríamos 10-3 x 1 = 0.001.
Desse modo, nesse computador simples, a variação de números "reais" que poderiam ser representados nesse computador, seria:
| - maior valor positivo em binário | 999 x 103 | = | 999000; | |
| - menor valor estritamente positivo em binário | 1 x 10-3 | = | 0.001. |
A primeira questão que aparece ao tratar números não inteiros no computador digital é a perda de precisão ou os erros numéricos. Por exemplo, mesmo em notação decimal o valor 1/3 não será representado perfeitamente, ele será registrado com algo semelhante a 0.3333 (se o computador utilizar 4 dígitos).
Um exemplo do problema numérico está ilustrado no exemplo abaixo, quando tentamos imprimir as somas de 0.1 até 0.9. Experimente copiar este trecho de código e rodar em C ou em Python, você deverá notar que o algoritmo nunca parará! Isso mesmo, laço infinito, pois como o computador utiliza notação binário e convertendo o decimal 0.1 para binário, é obtido um "binário periódico" (como a dízima periódica resultante do 1/3 que é 0.3...).
| C | Python | |
|---|---|---|
|
Entrada e saída de flutuantes em C e em Python
Em C deve-se utilizar o formatador %f para indicar que os bits devem ser tratados como número em ponto flutuante, enquanto em Python deve-se utilizar a função float(...), como indicado no exemplo abaixo.
| C | Python | |
|---|---|---|
|
Aos alunos estudando com a linguagem C, tomem um cuidado adicional: o compilador C aceita utilizar o formatador
de inteiro na leitura e na impressão de uma variável em flutuante. Ele trunca o valor, assim se tiver float x=1.5;
e fizer
Uma boa fonte para pesquisar é examinar o texto na WikiPedia: floating-point.
Leônidas de Oliveira Brandão
http://line.ime.usp.br
Alterações:
2022/09/02: ampla revisão, vários acertos em valores de maiores e menores valores positivos;
2020/08/10: novas seções iniciais;
2020/04/18: inserido nomes nas tabelas, correcao tab. 1 ("x+=1.0"->"x+=0.1")
2017/04/14: primeira versão