14. Matriz de Transformação Perspectiva

Nessa aula veremos como é possível definir uma matriz de transformação que aplique uma “distorção” perspectiva na construção do desenho 3D. Assim como fizemos com transformações afins, essa matriz tem dimensão \(4 \times 4\) e, como você já deve desconfiar, vamos representar pontos em coordenadas homogêneas no espaço projetivo. Lembre-se que esse espaço só utiliza pontos, não há vetores como no espaço afim.

14.1. A transformação de projeção perspectiva

Vamos supor, por enquanto, que os pontos a serem transformados estão todos estritamente à frente da câmera. Veremos que os objetos atrás da câmera devem eventualmente ser cortados, mas consideraremos isso mais tarde.

Agora considere a seguinte situação de visualização ilustrada na Figura Fig. 14.1, onde o centro de projeção corresponde à origem do sistema de coordenadas e que, normalmente, corresponde ao sistema de coordenadas da câmera que vai gerar a foto (desenho) da cena 3D. Vimos na aula passada como construir esse sistema usando a função lookAt(eye, at, up). Nessa situação a câmera aponta na direção \(-z\). Lembre-se que isso é necessário para que o sistema de coordenadas seja destro. O eixo \(x\) aponta para a direita do observador e o eixo \(y\) aponta para cima.

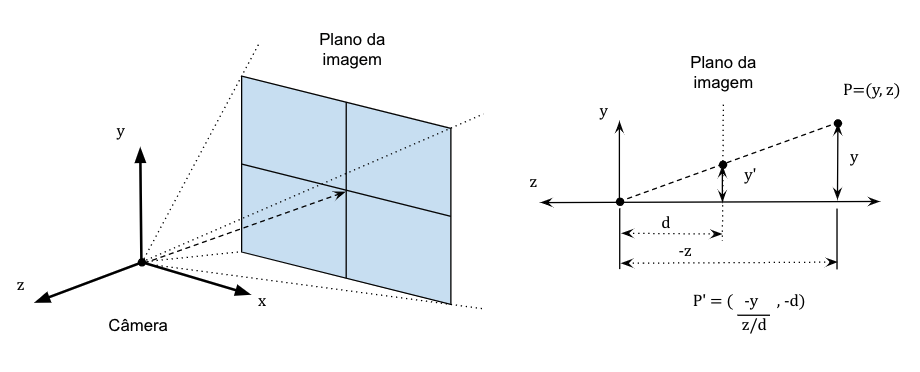
Fig. 14.1 Projeção perspectiva. No corte à direita, imagine que o eixo \(x\) aponta na sua direção.

Suponha que estamos projetando pontos em um plano de projeção ortogonal ao eixo \(z\) e localizado a uma distância \(d\) da origem na direção de \(-z\). Observe que \(d\) é dado como um número positivo, não negativo. Isso é consistente com as convenções do WebGL. Para simplificar nosso desenho e facilitar seu entendimento, vamos tomar uma vista lateral que mostra apenas os eixos \(y\) e \(z\), como mostrado na Figura Fig. 14.1 à direita. Dada a simetria da geometria, tudo o que fizermos para \(y\) pode ser feito da mesma forma com \(x\).

Considere um ponto \(P = (y, z)^T\) no plano. Note que \(z\) é negativo mas \(d\) é positivo. Onde esse ponto é projetado no plano da imagem? Seja \(P' = (y', z')^T\) as coordenadas da projeção de \(P\). Por similaridade de triângulos podemos determinar a seguinte relação:

\(\frac{y}{-z} = \frac{y'}{d}\).

E portanto o ponto projetado tem coordenada \(y' = y/(-z/d)\), com coordenada \(z = -d\) (no plano da imagem). No espaço 3D, um ponto com coordenadas \((x,y,z,1)^T\) é transformado para o ponto com coordenadas homogêneas

\(\begin{pmatrix}x/(-z/d) \\ y/(-z/d) \\ -d \\ 1\end{pmatrix}\).

Infelizmente, não existe uma matriz \(4 \times 4\) capaz de gerar esse resultado. Isso porque uma matriz representa uma transformação linear que mapeia um ponto \((x,y,z,1)^T\) para um ponto cujas coordenadas são da forma \(ax + by + cz + d\). O problema aqui é que \(z\) está no denominador.

Uma alternativa é usar uma matriz \(4 \times 4\) que gera um ponto equivalente, em relação às coordenadas homogêneas. Em particular, se multiplicarmos o vetor acima por (\(-z/d\)) obtemos:

\(\begin{pmatrix}x \\ y \\ z \\ -z/d\end{pmatrix}\).

As coordenadas desse vetor são todas funções lineares de \(x\), \(y\) e \(z\), e assim podemos escrever a transformação perspectiva em termos da seguinte matriz:

\(\begin{pmatrix}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & -1/d & 0\end{pmatrix}\).

Uma vez que tenhamos calculado as coordenadas de um ponto transformado (afim) usando \(P′ = M \cdot P\), aplicamos a normalização projetiva (ou divisão perspectiva) para determinar o ponto correspondente no espaço euclidiano.

\(M P = \begin{pmatrix}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & -1/d & 0\end{pmatrix} \begin{pmatrix}x \\ y \\ z \\ 1\end{pmatrix} = \begin{pmatrix}x \\ y \\ z \\ -z/d\end{pmatrix} \sim \begin{pmatrix}x/(-z/d) \\ y/(-z/d) \\ -d \\ 1\end{pmatrix}\).

Observe que caso \(z = 0\), há divisão por zero. No entanto, observe também que a projeção perspectiva mapeia pontos no plano \(xy\) no infinito.

14.2. Projeção em um volume de visualização

Você deve se lembrar que para desenhar em 2D no WebGL, devemos limitar nosso desenho ao quadrado de lado 2 definido pelos cantos (-1, -1) a (1,1). Vértices desenhados fora desse espaço normalizado são automaticamente recortados. Em 3D temos uma limitação semelhante, os objetos visíveis devem estar contidos no cubo de lado 2 definido pelos cantos (-1,-1,-1) a (1,1,1). Esse cubo define o volume de visualização canônico.

Você pode imaginar que seja natural limitar em \(xy\) pois o canvas (ou TV, papel etc) tem dimensões limitadas. Mas para que limitar em \(z\)? Pois a limitação do intervalo no eixo \(z\) facilita a criação de um buffer de profundidades, utilizado pelo WebGL para resolver o problema de oclusão, ou seja, dessa forma o WebGL pode desenhar os objetos mais próximos sobre os objetos mais distantes. A existência desse volume também não implica que somos obrigados a desenhar apenas dentro do volume. Apenas significa que, coisas fora do volume, serão recortadas para fora do desenho.

A projeção perspectiva juntamente com o problema de determinação da profundidade de cada objeto com relação ao observador e ainda eliminação de pontos fora do volume canônico pode ser feita de forma bastante elegante e eficiente, mas para isso precisamos considerar mais alguns elementos geométricos que definem um volume de visualização genérico na forma de um frustum (tronco de pirâmide) de base retangular, como ilustrado na Figura Fig. 14.2. A definição desse frustum nos ajuda a delimitar (recortar ou clip) a região da cena que deve ser mapeada para o volume de visualização canônico.

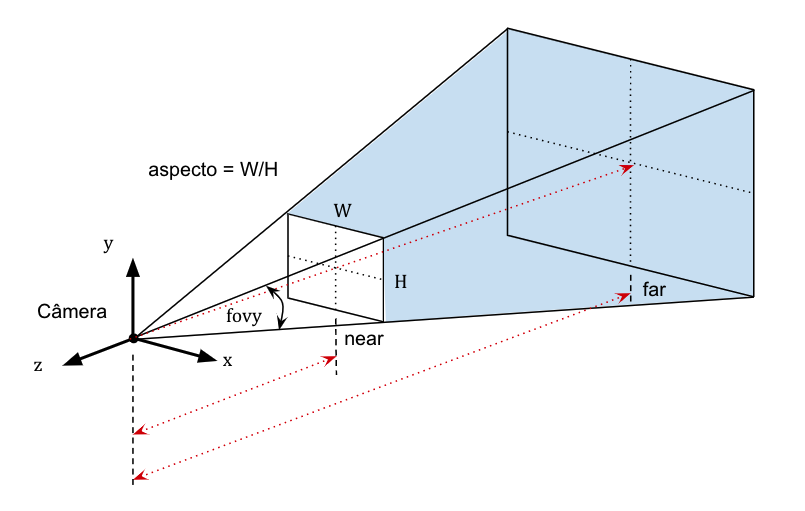
Fig. 14.2 Volume de visualização da projeção perspectiva.

O frustum é limitado pelos planos near e far. Isso significa que o observador (câmera) só consegue ver objetos além do plano near e até o plano far. Observe que, como temos um número limitado de bits para representar a profundidade, quanto maior a distância entre esses planos, menor será a precisão disponível para discriminar essas profundidades. Objetos (ou partes de objetos) fora desse intervalo são “cortados” para fora do volume normalizado (e portanto do desenho). O ápice da pirâmide corresponde ao centro de projeção da câmera (ou olho do observador).

Vamos assumir também que o centro da imagem (ou sensor da câmera) está alinhado com o eixo \(-z\), que é direção de visualização da câmera. Essa imagem tem altura \(H\) e largura \(W\). Vamos considerar apenas a razão de aspecto (aspect ratio) que é definida como \(aspecto = W/H\) na definição do frustum. Ao invés de definir a distância do sensor ao centro de projeção (comprimento focal), vamos considerar o campo de visão vertical fovy (vertical field-of-view), um ângulo que define a altura (ou abertura) vertical da pirâmide, como mostrado na Figura Fig. 14.2. Observe que a partir dos valores do aspecto e do fovy é possível derivar o campo de visão horizontal (ou fovx).

Assim como fizemos com a função lookAt(eye, at, up) na aula anterior, vamos ver como construir uma matriz de transformação perspectiva a partir desses parâmetros.

14.3. Construção da matrix de transformação perspectiva

Nessa seção vamos derivar a função perspective(fovy, aspect, near, far), que recebe os parâmetros que definem o frustum de visualização com descrito na seção anterior e retorna uma matriz de transformação perspectiva com profundidade que podemos usar para definir a matriz de projeção (ou ao menos parte dela). Se as características de projeção da câmera não se alterarem, essa matriz pode ser calculada uma única vez durante a inicialização do seu programa.

Vamos começar tentando entender o que significa perspectiva com profundidade. Recode que a transformação perspectiva que descrevemos anteriormente mapeia o ponto \((x, y, z, 1)^T\) para o ponto \((−x/(z/d), −y/(z/d), −d, 1)^T\). Observe que os dois últimos componentes deste vetor não transmitem nenhuma informação, pois eles são sempre os mesmos, não importa qual ponto é projetado.

Como vimos, ao invés de mapear todos os pontos para o plano da imagem em \(z = -d\), seria muito interessante manter a informação de distância do ponto à câmera (sua profundidade), para que possamos remover as superfícies escondidas devido à oclusão. Assim, ao invés de mapear para um plano, como a gente pode mapear para um volume?

Para isso vamos definir uma matriz que transforma um ponto de coordenadas \((x,y)\) segundo a projeção perspectiva mas que ainda conserve informação de profundidade em sua componente \(z\). Por isso chamamos essa transformação de perspectiva com profundidade. As componentes \((x,y)\) são então usadas para desenhar o objeto projetado e a coordenada \(z\) é usada na remoção das superfícies ocultas. Acontece que essas informações de profundidade estão sujeitas a uma distorção não linear. No entanto, essa informação ainda é útil pois a ordem de profundidade é preservada, ou seja, os pontos mais distantes da câmera (em termos de suas coordenadas \(z\)) apresentam valores de profundidade maiores do que os pontos mais próximos.

Vamos começar de forma simples, considerando, como de costume, que o centro de projeção da câmera corresponde à origem do sistema de coordenadas e que a câmera está voltada para baixo, na mesma direção do eixo \(-z\). Vamos supor também que o plano de projeção está localizado em \(z = -1\). Considere a seguinte matriz:

\(M = \begin{pmatrix}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & \alpha & \beta\\ 0 & 0 & -1 & 0\\ \end{pmatrix}\).

Quando \(M\) é aplicada a um ponto \(P\) com coordenadas homogêneas \((x, y, z, 1)^T\), temos:

\(M \cdot P = \begin{pmatrix}x \\ y\\ \alpha z + \beta\\ -z\end{pmatrix} \sim \begin{pmatrix} -x/z \\ -y/z \\ -\alpha - \beta/z\\ 1\end{pmatrix}\).

Observe que as coordenadas \(x\) e \(y\) recebem a projeção perspectiva correta (lembrando que \(z < 0\) já que estamos olhando para baixo ao longo do eixo \(-z\)) e o valor da profundidade é

\(z' = -\alpha -\beta z\).

Dependendo dos valores que escolhemos para \(\alpha\) e \(\beta\), esta é uma função monotônica (não linear) de \(z\). Em particular, a profundidade aumenta à medida que os valores de \(z\) diminuem (já que vemos o eixo \(z\) negativo), portanto, se definirmos \(\beta < 0\), o valor da profundidade \(z'\) será uma função monotonicamente crescente da profundidade.

De fato, escolhendo \(\alpha\) e \(\beta\) corretamente, os valores de profundidade podem ser ajustados para que fiquem dentro de qualquer faixa de valores que nos seja conveniente. Veremos a seguir como esses valores devem ser escolhidos.

14.4. Volume de Visualização Canônico

Ao aplicar a transformação perspectiva, todos os pontos no espaço projetivo são transformados. Isso inclui pontos que não estão dentro do frustum de visualização (por exemplo, pontos atrás do observador). Uma das tarefas importantes a serem executadas pelo sistema, antes da divisão de perspectiva (quando todas as coisas ruins podem acontecer) é recortar partes da cena que não estão dentro do frustum.

Podemos ajudar a transformação perspectiva com profundidade de forma elegante (escolhendo valores adequados para \(\alpha\) e \(\beta\)) para que o frustum de visualização genérico seja mapeado para o volume de visualização canônico independentemente da forma como tenha sido definido pelo usuário. Como o processo de recorte é aplicado sempre sobre o volume canônico, isso permite utilizar algoritmos de recorte (clipping) mais simples e eficientes. .. O recorte é realmente realizado em um espaço de coordenadas homogêneas (ou seja, 4-dimensional) imediatamente antes da divisão em perspectiva. No entanto, descreveremos o volume da visão canônica em termos de como ele aparece após a divisão da perspectiva. (Deixaremos como exercício descobrir como é antes da divisão de perspectiva.)

Desejamos portanto que os planos near e far sejam mapeados para as faces \(z=-1\) e \(z=1\) do volume canônico, ou seja, pontos mapeados para \(z=1\) são os mais distantes do observador. A orientação dos demais eixos deve se manter, ou seja, \(x\) aponta para a direita e \(y\) para cima.

Para escolher valores adequados para \(\alpha\) e \(\beta\), vamos então considerar que desejamos mapear pontos no plano em \(z = -n\) para \(z' = -1\) e pontos no plano \(z = -f\) para \(z' = +1\), onde n e f denotam as distâncias para os planos de recorte near e far. Com isso temos o seguinte sistema de equações:

\(-1 = -\alpha - \frac{\beta}{-n} \;\;\;\;\;\) e \(\;\;\;\;\;1 = -\alpha - \frac{\beta}{-f}\).

Resolvendo esse sistema temos:

\(\alpha = \frac{f + n}{n - f} \;\;\;\;\;\) e \(\;\;\;\;\; \beta=\frac{2 f n}{n - f}\).

14.5. Matriz de transformação perspectiva

Para montar a matriz de transformação perspectiva completa, que você pode utilizar em seus desenhos 3D, considere a razão de aspecto denominada por \(a\) e o \(fovy = \theta\) em radianos. Seja \(c = cot( \theta / 2)\). Seja também \(n\) e \(f\) as distâncias para os planos de recorte near e far, respectivamente, considerando todos esses valores positivos. A matriz calculada pela função perspective() pode ser definida como:

\(M = \begin{pmatrix}c/a & 0 & 0 & 0\\ 0 & c & 0 & 0 \\ 0 & 0 & \frac{f+n}{n-f} & \frac{2fn}{n-f} \\0 & 0 & -1 & 0\end{pmatrix}\).

Assim, essa transformação mapeia um ponto \(P = (x, y, z, 1)^T\) para:

\(M \cdot P = \begin{pmatrix}cx/a \\ cy \\ ((f+n)z + 2fn)/(n-f) \\ -z\end{pmatrix} \sim \begin{pmatrix}-cx/(az) \\ -cy/z \\ (-(f+n) - (2fn/z))/(n-f) \\ 1\end{pmatrix}\).

Ficou curioso para saber de onde surgiu esse mapeamento estranho? Observe que, além dos fatores de escala, isso é muito semelhante à matriz de perspectiva com profundidade fornecida anteriormente (já com os nossos valores de \(\alpha\) e \(\beta\)). Os elementos \(c/a\) e \(c\) na diagonal estão presentes para dimensionar o retângulo arbitrário da base do frustum no quadrado de lado 2, como veremos a seguir.

14.6. Exemplos: mas será que isso funciona?

Para ver que isso funciona, mostraremos que os cantos do frustum genérico são mapeados para os cantos do volume de visualização canônico (e vamos confiar que tudo entre eles se comporta bem). Na Figura Fig. 14.3 mostramos uma vista lateral que mostra apenas o plano \(yz\). Como a janela tem a proporção \(a = W/H\), segue-se que para os pontos na borda superior direita do frustum de visualização (em relação à perspectiva do observador) temos \(x/y = a\) e, portanto, \(x = ay\).

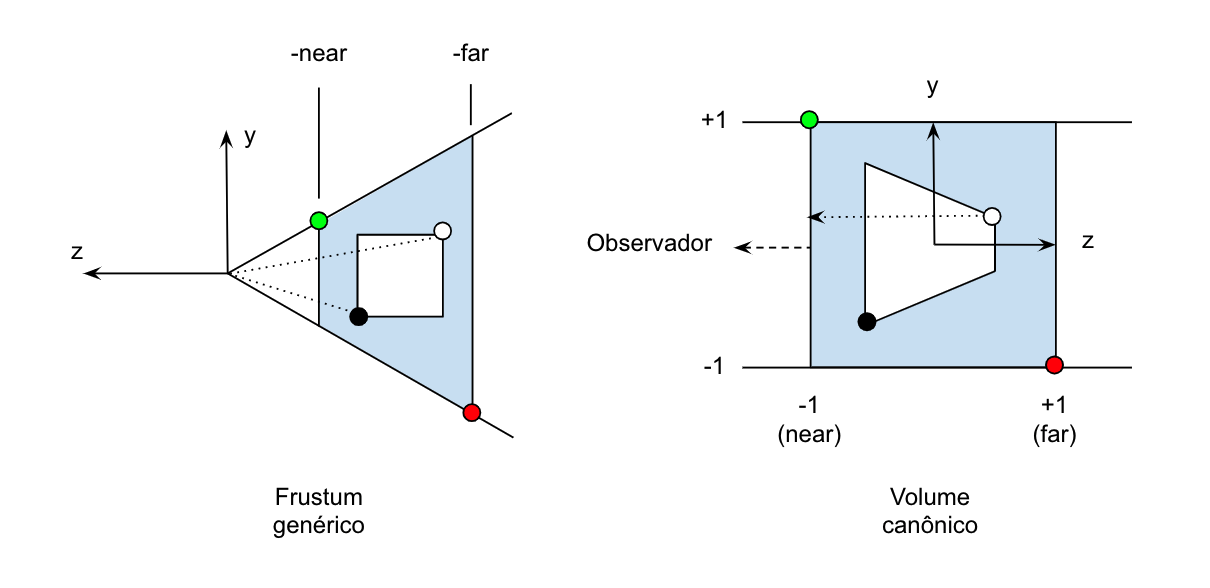
Fig. 14.3 Perspectiva com profundidade e o volume de visualização canônico.

Considere um ponto que fica no lado superior da pirâmide (ponto verde na figura acima). Temos \(-z/y = cot \theta/2 = c\), implicando que \(y = -z/c\). Como o ponto pertence ao plano de corte near, teremos \(z = -n\) e, portanto, \(y = n/c\) (considere a altura do triângulo formado pelo topo da pirâmide). Além disso, se assumirmos que o ponto está no canto superior direito (em relação ao observador), então \(x = ay = an/c\). Assim, as coordenadas homogêneas do ponto no canto superior no plano de recorte near (ponto verde) são \((an/c, n/c, -n, 1)^T\). Aplicando a transformação sobre esse ponto temos:

\(M \begin{pmatrix}an/c \\ n/c \\ -n \\ 1\end{pmatrix} = \begin{pmatrix}n \\ n \\ \frac{-n(f+n)}{n-f} + \frac{2fn}{n-f} \\n\end{pmatrix} \sim \begin{pmatrix}1 \\ 1 \\ \frac{-(f+n)}{n-f} + \frac{2f}{n-f} \\1\end{pmatrix} = \begin{pmatrix}1 \\ 1\\ -1\\ 1\end{pmatrix}\).

Note que esse ponto corresponde ao canto superior direito do volume de visualização canônico no plano near (\(z=-1\)).

Da mesma forma, considere um ponto que se encontra na parte inferior do frustum (ponto vermelho na figura). Temos \(-z/(-y) = cot \theta/2 = c\), implicando que \(y = z/c\). Se tomarmos o ponto como estando no plano far, então temos \(z = -f\), e então \(y = -f/c\). Além disso, se assumirmos que o ponto está no canto inferior esquerdo do frustum (em relação à posição do observador), então \(x = -af/c\). Assim, as coordenadas homogêneas do canto inferior no plano de recorte far (ponto vermelho) são \((-af/c, -f/c, -f, 1)^T\). Aplicando a transformação sobre esse ponto temos:

\(M \begin{pmatrix}-af/c \\ -f/c \\ -f \\ 1\end{pmatrix} = \begin{pmatrix}-f \\ -f \\ \frac{-f(f+n)}{n-f} + \frac{2fn}{n-f} \\f\end{pmatrix} \sim \begin{pmatrix}-1 \\ -1 \\ \frac{-(f+n)}{n-f} + \frac{2n}{n-f} \\1\end{pmatrix} = \begin{pmatrix}-1 \\ -1\\ 1\\ 1\end{pmatrix}\).

Que corresponde ao canto inferior esquerdo do volume de visualização canônico no plano far (\(z = 1\)).

14.7. Onde estamos e para onde vamos?

Vimos que a projeção perspectiva na verdade é uma transformação não linear que não possui uma forma matricial direta para ser calculada. Mas aplicando os fundamentos de geometria projetiva introduzidos na última aula vimos que é possível construir uma matriz para aplicar a projeção perspectiva e que, após a divisão perspectiva, obtemos as coordenadas projetadas sobre o plano da imagem. Essa transformação no entanto elimina a informação de profundidade dos vértices, dificultando o desenho das partes visíveis e/ou remoção das partes ocultas por oclusão dos objetos que estão mais próximos à câmera.

Para resolver isso, modificamos a matriz de transformação perspectiva para incluir também informação de profundidade que possa ser utilizada para ordenar os objetos segundo sua profundidade com relação à câmera. Para isso, utilizamos um frustum definido por quatro parâmetros: fovy, a (razão de aspecto),e os planos near e far. Na prática, podemos utilizar a função perspective(fovy, a, near, far) para calcular a matriz de projeção perspectiva com profundidade.

Na próxima aula, vamos ver alguns exemplos de aplicação dessa matriz no WebGL.

14.8. Para saber mais

• Capítulo 5 do livro “Interactive Computer Graphics”, 8a edição, de Edward Angel e Dave Shreiner.
• Aula 10 das notas de aula do Prof. Dave Mount.