Livro-texto: Não há um livro-texto no sentido formal. Os mais utilizados neste curso serão os três primeiros itens da bibliografia abaixo.

Bibliografia:

• J. Milnor, Dynamics in One Complex Variable, 3^rd edition, Annals of Mathematics Studies 160, Princeton University Press, 2006.
• E. de Faria & W. de Melo, Mathematical Tools for One-Dimensional Dynamics, Cambridge Studies in Advanced Mathematics 115, Cambridge University Press, 2008.
• L. Carleson & T. Gamelin, Complex Dynamics, Undergraduate Texts in Mathematics, Springer-Verlag, 1993.
• A. Beardon, Iteration of Rational Functions, Graduate Texts in Mathematics 132, Springer-Verlag, 1991.
• C. McMullen, Complex Dynamics and Renormalization, Annals of Mathematics Studies 135, Princeton University Press, 1994.
• S. Morosawa, Y. Nishimura, M. Tanuguchi & T. Ueda, Holomorphic Dynamics, Cambridge Studies in Advanced Mathematics 66, Cambridge University Press, 2000.

Horário e local das aulas: Segundas e Quintas, das 14:00 às 16:00, sala 243 do IME-Bloco A.

Programa resumido do curso:

1. Preliminares: Funções Holomorfas e Superfícies de Riemann
   • Lemas de Schwarz e Schwarz-Pick.
   • Automorfismos complexos; Aut(D), Aut(ℂ), Aut().
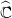   • Superfícies de Riemann: definição e exemplos.
   • Recobrimentos holomorfos; teorema da uniformização (enunciado).
   • Superfícies hiperbólicas; métrica de Poincaré; lema de Ahlfors-Schwarz-Pick.
   • Famílias normais e teorema de Montel.
2. Dinâmica de Transformações Holomorfas
   • Propriedades básicas: valores singulares e críticos, Teorema de Riemann-Hurwitz.
   • Tipos de pontos periódicos e suas dinâmicas locais.
   • Dinâmica em superfícies hiperbólicas.
   • Conjuntos de Fatou e Julia: propriedades gerais, exemplos, conjuntos de Julia hiperbólicos.
   • Os casos de polinômios, de funções racionais e de funções inteiras.
3. Métodos quase-conformes
   • Homeomorfismos quase-conformes.
   • Teorema de Ahlfors-Bers; extensão de Beurling-Ahlfors.
   • Não-existência de domínios errantes: teorema de Sullivan para funções racionais.
   • Transformações do tipo polinomial: straightening theorem de Douady-Hubbard.
   • Cirurgia quase-conforme.
4. Tópicos Opcionais¹
   • Funções inteiras e domínios de Baker.
   • Demonstração do teorema de Ahlfors-Bers.
   • Movimentos holomorfos: o λ-lema de Mañé-Sad-Sullivan.
   • Estabilidade estrutural em famílias holomorfas de aplicações racionais.
   • Polinômios quadráticos: o conjunto de Mandelbrot; conectividade e conectividade local; os teoremas de Douady-Hubbard e de Yoccoz.
   • Aspectos ergódicos da iteração de funções racionais ou transcendentes.
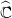