O que é E8?

Veja a seguinte reportagem onde você pode encontrar informação geral sobre este grupo.

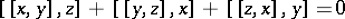
Descrição: O tema principal de estudo desta disciplina são grupos de Lie e álgebras de Lie. Grupos de Lie podem ser pensados como “simetrias globais”, enquanto que “simetrias infinitesimais” dão origem às álgebras de Lie. As ferramentas principais que usaremos são topologia, geometria diferencial e álgebra. Os assuntos abordados neste curso fornecem ferramentas que permitem entender problemas que aparecem em diversas áreas da matemática, por exemplo: invariantes, simetrias de equações diferenciais, teoria de números, análise harmônica, sistemas dinâmicos, entre outros. Além disso, grupos de Lie e suas álgebras de Lie aparecem de maneira natural em mecânica clássica, teorias de calibre, teoria de cordas, etc.

Os pré-requisitos para esta disciplina são: Topologia geral, Teoria de Grupos, Geometria Diferencial. 

Aulas: Terças e Quintas 10:30-12:00 no Anfiteatro A.

Atendimento a alunos: Sexta-feira às 17:00 após os Seminários de Geometria e Álgebra.

Avaliação: Listas de exercício. Uma prova escrita que será realizada na quinta-feira 17 de novembro às 10:30. Além disso o aluno deverá elaborar um projeto escrito a ser apresentado no curso. O projeto deve desenvolver um tema, de interesse do aluno (aprovado pelo professor), relacionado com a disciplina. Algumas sugestões de projeto podem ser encontradas em projeto.pdf.

Programação das apresentações:

1. • 06 de dezembro - 10:00-10:50: “Extensões centrais de álgebras de Lie” (Mayumi)
   

                              - 11:00-11:50: “Espaços homogêneos e órbitas coadjuntas” (Lilian)

1. • 08 de dezembro -10:00-10:50: “Representações do grupo de Heisenberg” (Yohny)
   

                              -11:00-11:50: “Ações isométricas e esferas exóticas” (Andrés)

1. • 13 de dezembro -10:00-10:50: “Geodésicas em grupos de Lie compactos” (William)
   

                               -11:00-11:50: “Recobrimentos de SO(n)” (Fernando)

1. • 15 de dezembro -10:00-10:50: “Grupos algébricos” (Cristian)
   

                               -11:00-11:50: “Espaço de moduli de representações de quivers” (Germán)

Ementa: Os tópicos que abordaremos incluem:

1. 1. Conceitos básicos de variedades diferenciáveis: variedades, subvariedades, fibrado tangente, campos de vetores, colchete de Lie de campos, Teorema de Frobenius (enunciado).
   

2. 2. Grupos de Lie, subgrupos, homomorfismos.
   

3. 3. Grupos de Lie clássicos.
   

4. 4. Álgebras de Lie, subálgebras, homomorfismos.
   

5. 5. Álgebras de Lie clássicas.
   

6. 6. Teoremas fundamentais da Teoria de Lie.
   

7. 7. Ações de grupos de Lie.
   

8. 8. Representações de grupos e álgebras de Lie.
   

9. 9. Grupos de Lie compactos: Toros maximais, Grupo de Weyl, subgrupos de Cartan.
   

10. 10. Sistemas de raízes: câmaras de Weyl, Diagramas de Dynkin, sistemas de raízes de grupos clássicos.
    

11. 11. Tópicos adicionais.
    

Bibliografia: O curso será baseado em alguns dos seguintes livros. Todos contêm bastante informação sobre grupos de Lie e álgebras de Lie.

1. 1. Duistermaat, J. J., Kolk, J., Lie Groups, Universitext - Springer Verlag.
   

2. 2. Fulton, W., Harris, J., Representation Theory, GTM - Springer Verlag.
   

3. 3. Humprheys, J., Introduction to Lie algebras and Representation Theory, GTM - Springer Verlag.
   

4. 4. San Martin, L., Álgebras de Lie, Editora Unicamp.
   

5. 5. Spivak, M., A comprehensive introduction to differential geometry, Vol. 1.
   

6. 6. Varadarajan, V. S., Lie groups, Lie algebras and their representations, GTM - Springer Verlag.
   

7. 7. Warner, F., Foundations on differentiable manifolds and Lie groups, GTM - Springer Verlag.
   

Listas:

1. 1. Lista1.pdf
   

2. 2. Lista2.pdf  (Entregar dia 27/09 no horário de aula)
   

3. 3. Lista3.pdf  (Entregar dia 11/10 no horário de aula)
   

4. 4. Lista4.pdf  (Entregar dia 25/10 no horário de aula)
   

5. 5. Lista5.pdf  (Entregar dia 17/11 no horário de aula)