Descrição: Esta disciplina é fundamental na formação de cientistas, em particular na formação de Físicos. O Cálculo é uma ferramenta que permite estudar fenómenos que dependem do tempo numa escala infinitesimal. Nesta disciplina existem dois conceitos muito importantes: derivada e integral. Ambos os conceitos são muito úteis em Física, e.g. a velocidade instantânea de uma partícula que anda em linha reta pode ser calculada derivando a posição da partícula, ou o trabalho de uma força é uma medida obtida calculando uma integral. Os conceitos de derivada e integral interagem através do Teorema Fundamental do Cálculo. O objetivo desta disciplina consiste em introduzir os conceitos de derivada e integral, estudando tanto os fundamentos teóricos como as técnicas de derivação e integração. Ao longo do curso, discutiremos vários exemplos de interesse físico.

Aulas: Terças e Sextas das 7:30 às 9:30 na sala PA03

Observação: No período compreendido entre 05-09 de novembro, as aulas serão ministradas pelos professores Carlos H. dos Santos e Eduardo Hoefel. No período compreendido entre 26 de novembro e 01 de dezembro o Prof. Eduardo Hoefel realizará as aulas.

Aviso: Na sexta-feira dia 16 de novembro, teremos aulas normalmente.

Atendimento a alunos: Quarta-feira das 17:00 às 18:00 na minha sala no Departamento de Matemática.

Avaliação: 3 provas cujas datas são as seguintes:

Prova 1: 18 de dezembro de 2012. Notas aqui

As notas da prova estão prontas e serão divulgadas em breve, bem como a solução da prova. Na sexta 21 de dezembro não haverá aula.

Prova 2: 8 de fevereiro de 2013

Prova 3: 15 de março de 2013

Prova Final: 22 de março de 2013

Prova de segunda chamada conforme às regras da universidade. É responsabilidade do aluno solicitar a segunda chamada assim como apresentar os devidos documentos comprobatórios. Não haverá prova substitutiva!

Ementa: Os tópicos que estudaremos nesta disciplina são:

Parte 1: Continuidade

1. • Funções
   

2. • Limite de funções
   

3. • Funções contínuas
   

Parte 2: Diferenciabilidade

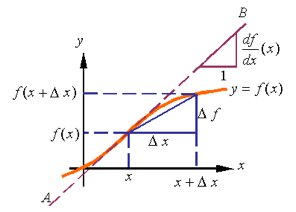
1. • Conceito de derivada
   

2. • Derivadas de ordem superior
   

3. • Fórmula da Taylor
   

4. • Pontos críticos: máximos, mínimos e pontos de inflexão
   

5. • Aplicações
   

Parte 3: Integrabilidade

1. • Conceito de integral
   

2. • Teorema fundamental do cálculo
   

3. • Métodos de integracão: integração por partes, mudança de variáveis.
   

4. • Aplicações
   

Parte 4: Séries Numéricas

1. • Convergência de séries numéricas
   

2. • Séries de potências
   

3. • Série de Taylor
   

Veja o programa oficial aqui

Referências: Algumas referências são:

1. • Guidorizzi, H.L, “Curso de cálculo - Vol1”
   

2. • Spivak, M., “Calculus”
   

Listas: Lembrem que existe horário de atendimento onde podem tirar dúvidas sobre as listas. Também podem consultar aos monitores de cálculo.

1. • Lista1
   

2. • Lista2