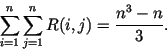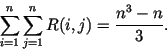Next: About this document ...
MAC-IME-USP CARLOS EDUARDO FERREIRA
SALA 297A TEL.: 3091 6140
E-MAIL cef@ime.usp.br
MAC 5711 - Análise de Algoritmos
Terceira lista de exercícios - entrega 20 de maio de 2003
- Pensando um pouco sobre árvores de busca binária formulei a seguinte
proposição. Suponha que ao buscar um elemento
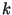 numa árvore de busca
binária, a busca termina numa folha
numa árvore de busca
binária, a busca termina numa folha 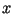 . Considere os conjuntos:
. Considere os conjuntos: 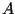 (os elementos à
esquerda do caminho da raiz até
(os elementos à
esquerda do caminho da raiz até 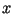 ),
), 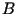 (os elementos no caminho da raiz a
(os elementos no caminho da raiz a
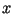 ) e
) e 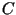 (os elementos à direita do caminho). Então, para todo elemento
(os elementos à direita do caminho). Então, para todo elemento
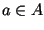 ,
, 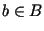 e
e 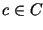 vale que
vale que 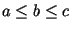 . Dê um contra-exemplo
que seja o menor possível para essa proposição.
. Dê um contra-exemplo
que seja o menor possível para essa proposição.
- Qual é o maior número possível de nós internos numa árvore rubro-negra
de altura
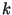 ? E o menor número possível?
? E o menor número possível?
- Descreva uma árvore rubro-negra com
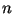 elementos (folhas nil não
contam) em que a razão entre o número de nós vermelhos e o número de nós
pretos internos seja a maior possível. Qual é o valor dessa razão? O mesmo
para a menor razão possível.
elementos (folhas nil não
contam) em que a razão entre o número de nós vermelhos e o número de nós
pretos internos seja a maior possível. Qual é o valor dessa razão? O mesmo
para a menor razão possível.
- Seja
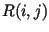 o número de vezes que uma entrada da matriz
o número de vezes que uma entrada da matriz ![$opt[i,j]$](img12.png) é
referenciada no algoritmo que acha a solução ótima do problema de
multiplicação de cadeia de matrizes. Mostre que o número de referências para a
tabela inteira é
é
referenciada no algoritmo que acha a solução ótima do problema de
multiplicação de cadeia de matrizes. Mostre que o número de referências para a
tabela inteira é
Você pode usar o seguinte fato:
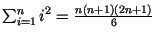 .
.
- Uma triangulação de um polígono convexo é uma subdivisão do seu interior
por diagonais que não se cruzam em regiões triangulares. Prove que toda
triangulação de um polígono convexo de
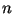 vértices usa
vértices usa 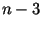 diagonais e
divide o polígono em
diagonais e
divide o polígono em 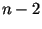 triângulos.
triângulos.
- Escreva um algoritmo que recebe como entrada os vértices de um polígono
convexo (dados em ordem ``contra o sentido dos ponteiros do relógio'') e
encontra uma triangulação deste polígono que tenha custo mínimo. O custo de
uma triangulação é dado pela soma dos custos dos triângulos que a compõem e o
custo de um triângulo é igual à soma dos comprimentos de seus lados.
- Considere o seguinte problema. Um ladrão entrou em um salão com uma
mochila capaz de carregar
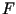 quilos. Neste salão, cada um dos vários itens
que ele poderia roubar tem peso
quilos. Neste salão, cada um dos vários itens
que ele poderia roubar tem peso 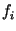 e valor
e valor 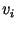 . O ladrão resolveu seguir
uma estratégia gulosa, roubando os itens de maior valor até que nada mais
coubesse na sua mochila.
. O ladrão resolveu seguir
uma estratégia gulosa, roubando os itens de maior valor até que nada mais
coubesse na sua mochila.
a. Mostre que a estratégia do ladrão não produz a solução ótima para toda
instância de entrada possível.
b. Construa uma instância com 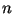 itens em que a estratégia do ladrão é
ótima.
itens em que a estratégia do ladrão é
ótima.
c. É possível garantir que se 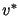 é o valor do melhor roubo possível com
aquela mochila, existe uma constante
é o valor do melhor roubo possível com
aquela mochila, existe uma constante
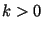 tal que a estratégia do ladrão produz uma
solução de valor maior ou igual a
tal que a estratégia do ladrão produz uma
solução de valor maior ou igual a 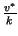 . Justifique detalhadamente
sua resposta.
. Justifique detalhadamente
sua resposta.



Next: About this document ...
Carlos Eduardo Ferreira
2003-04-30