Next: About this document ...
![]()
![]()
![]()
Next: About this document ...
MAC-IME-USP CARLOS EDUARDO FERREIRA
SALA 297A TEL.: 818 6140
E-MAIL cef@ime.usp.br
Primeira Prova
Esta prova será resolvida em duas partes. A primeira parte se encerra em duas horas, e a esta parte será atribuída uma nota . Você poderá entregar uma nova versão da prova até o dia 30 de setembro, às 14 horas. As questões que você não deseja alterar devem ser indicadas nesta segunda parte. A segunda parte receberá uma nota . A nota final da prova será dada por .
para at'e faça para at'e faça para at'e faça se então .
Ajuda: .

 .
.Mostre que, para todo , existe uma árvore geradora mínima que contém .
Usando uma formulação do problema como um Problema de Transporte encontre condições necessárias e suficientes (se possível, uma que seja necessária e suficiente ao mesmo tempo) para que um vetor não seja um vetor de pontuação.
Em uma iteração do método simplex para redes tem-se uma solução árvore viável correspondente à árvore desenhada abaixo. Sabe-se que o arco está em . Complete as tabelas abaixo após incluir o arco na árvore e retirar algum arco usando a regra de Cunningham para evitar ciclagem (todos os arcos têm custo igual a 1):

| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| pred | - | 1 | 1 | 3 | 4 | 5 | 5 | 7 | 7 | 5 | 3 | 11 | 12 | 13 | 12 |
| suc | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 1 |
| y | 0 | ||||||||||||||
| 0 |
| arcos | (3,4) | (4,5) | (7,5) | (7,9) | (12,11) | (3,11) | (12,9) | outros |
| x | 5 | 5 | 5 | 6 | 8 | 5 | 0 | 5 |
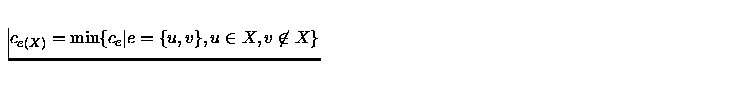 e o correspondente problema perturbado
,
e o correspondente problema perturbado
,
 onde dado um
,
para a raiz e
para todo
.
onde dado um
,
para a raiz e
para todo
.
Mostre que
a. Toda solução árvore viável de é não degenerada.
b. Uma árvore é viável em se e só se é fortemente viável em .
Carlos Eduardo Ferreira