DCC-IME-USP CARLOS EDUARDO FERREIRA JOSÉ COELHO DE PINA

SALA 297A TEL.: 818 6140 SALA 164B TEL.: 818 6295

E-MAIL cef@ime.usp.br E-MAIL coelho@ime.usp.br

MAC-115 - Introdução à Computação

INSTITUTO DE QUÍMICA - PRIMEIRO SEMESTRE DE 2000

Exercício-Programa 1 Entrega: 27 de abril de 2000

A mesma química do Exercício-Programa 1 (ela novamente ...), professora do IQ-USP, deseja obter a curva de calibração do composto secreto blá-blá-blá. Ela preparou várias amostras com concentrações diferentes de blá-blá-blá e leu as absorbâncias de cada amostra em um espectrofotômetro, no comprimento de onda de máxima absorbância deste composto. As concetrações e as respectivas absorbâncias foram colocadas em uma tabela e digitadas por um estagiário (quem mais ...) em um arquivo. Sabendo que no intervalo estudado a relação entre as concentrações das amostras e as absorbâncias é linear, a tal professora deseja um programa que determine a equação da reta y=mx +b que melhor aproxima os dados colhidos, onde o eixo y das ordenadas representa a absorbância e o eixo x das abscissas representa a concetração das amostras.

Preocupada em ter certeza de obter um programa confiável e muito bem feito, a professora resolveu ordenar que os alunos de MAC-115 façam um programa que recebe uma seqüência de pares de pontos e determina a reta que mais se aproxima desses pontos, utilizando o método dos mínimos quadrados, que está descrito logo a seguir.

Método dos mínimos quadrados

Nosso objetivo é aproximar uma função f, para a qual só conhecemos os valores em alguns pontos, por uma reta utilizando o método dos mínimos quadrados. Este caso particular da aplicação do método é conhecido pelo nome de regressão linear.

A função f será dada através de uma tabela de pontos $(x_1,y_1), (x_2,y_2), \ldots, (x_n,y_n)$ do seu gráfico (ou seja, y_i = f(x_i) $(i=1,\ldots,n)$).

Aproximar uma função f tabelada nos pontos $x_1,\ldots,x_n$ pelo método dos mínimos quadrados significa determinar os parâmetros m e b da reta y = mx + b de modo que a soma das distâncias dos pontos dados até a reta obtida seja mínima. A Figura 1 mostra a reta y = 1.1x - 0.2 que aproxima a função f dada através dos pontos (0,0), (1,1), (2,1), (3,4), (4,4).

Figure: Aproximação de um conjunto de pontos por uma reta.

O chamado coeficiente angular m e coeficiente linear b da reta y =mx + b que melhor aproxima os pontos $(x_1,y_1),\ldots,(x_n,y_n)$ podem ser obtidos resolvendo-se o seguinte sistema de equações lineares:

$$\begin{array}{lclcl} b \times n &+& m \times (\sum_{i=1}^n ... ...s (\sum_{i=1}^n x_i^2) & = & \sum_{i=1}^n x_i y_i \end{array}$$

Pela regra de Cramer sabemos que a solução do sistema acima é dada por:

$$\begin{eqnarray*} b & = & \frac{(\sum_{i=1}^n y_i) \times (\sum_{i=1}^n x_i^2) ... ...{i=1}^n x_i^2) - (\sum_{i=1}^n x_i) \times (\sum_{i=1}^n x_i)} \end{eqnarray*}$$

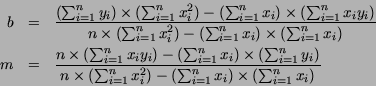
Para o exemplo da Figura 1 temos que

$$\begin{array}{c\vert ccccc} x~\mbox{(concentração)} & 0 & 1 ... ... \hline y~\mbox{(absorbância)} & 0 & 1 & 1 & 4 & 4 \end{array}$$

e portanto

$$\begin{eqnarray*} \sum_{i=1}^n x_i & = & 0 + 1 + 2 + 3 + 4 = 10 \\ \sum_{i=1}^n... ...16 = 30 \\ \sum_{i=1}^n x_i y_i & = & 0 + 1 + 2 + 12 + 16 = 31 \end{eqnarray*}$$

Finalmente, usando as fórmulas acima obtemos

$$\begin{eqnarray*} b & = & \frac{10 \times 30 - 10 \times 31}{5 \times 30 - 10 \... ...0 \times 10}{5 \times 30 - 10 \times 10} = \frac{11}{10} = 1.1 \end{eqnarray*}$$

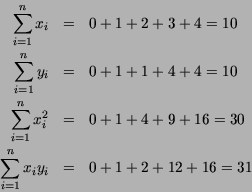
O quê o seu programa deve fazer

O seu programa deverá ler um seqüência de pontos de um arquivo, como descrito abaixo, e calcular os coeficientes m e b da reta y = mx + b que melhor aproxima os pontos dados.

Exemplo de entrada para o seu programa (conteúdo do arquivo de dados):

 
0  0 
1  1
2  1
3  4
4  4

Exemplo de saída fornecida pelo programa para os dados acima:

Aproximacao de uma reta pelo métodos dos mínimos quadrados

Entre com o nome do arquivo de dados: dados.txt
x1 =   0.000 y1 =   0.000
x2 =   1.000 y2 =   1.000
x3 =   2.000 y3 =   1.000
x4 =   3.000 y4 =   4.000
x5 =   4.000 y5 =   4.000


[      5   10.000] b = [ 10.000]
[ 10.000   30.000] m = [ 31.000]

denominador =  50.000.

A equacao da reta e' y = (  1.100) x + ( -0.200).

Esqueleto do seu programa

Para ler os dados de um arquivo use o seguinte `esqueleto' de programa

#include <stdio.h>

#define TAM_NOME 100

int main(void) {
  FILE *arqentrada;
  char nome[TAM_NOME];
  double x, y, m, b;

  /* outras declaracoes que voce julgar necessarias */
  [ ... ]

  printf("\n\nAproximacao de uma reta pelo metodos dos minimos quadrados\n\n");
  printf("Entre com o nome do arquivo de dados: ");
  scanf("%s", nome);

  if ((arqentrada = fopen(nome,"r")) == NULL) {
    printf("Arquivo %s nao foi encontrado\n\n", nome);
return 1;
  }

  while (!feof(arqentrada)) {
    /* leitura do proximo ponto */ 
    fscanf(arqentrada,"%lf %lf ", &x, &y); /* importante: deixar espaco
em branco apos %lf */
printf("x = %7.3f y = %7.3f\n", x, y);

    /* trecho do seu programa */
    [ ... ]
  } 

  /* trecho do seu programa */
  [ ... ] 

  printf("A equacao da reta e' y =(%7.3f) x + (%7.3f).\n\n\n", m, b); 

  fclose(arqentrada); 
  return 0;
}