


Next: About this document ...
MAC-IME-USP CARLOS EDUARDO FERREIRA
SALA 297A TEL.: 818 6140
E-MAIL cef@ime.usp.br
Geometria Computacional
Terceira Lista de Exercícios - Entrega 24 de novembro de 1999
- 1.
- No problema de determinar o fecho convexo de n pontos dados
on line, os pontos são dados um a um, sem uma ordem
pré-estabelecida. Deseja-se a cada ponto dado calcular o fecho convexo
do conjunto até então. Descreva um algoritmo para resolver esse
problema e faça uma análise da complexidade desse algoritmo.
- 2.
- Descreva um algoritmo linear que receba dois polígonos convexos
(não necessariamente disjuntos) e calcula o seu fecho convexo.
- 3.
- Descreva um algoritmo
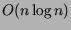 que receba dois polígonos
convexos com n e m vértices (
que receba dois polígonos
convexos com n e m vértices (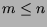 )
e verifica se os polígonos
são disjuntos. [Dá para fazer em tempo linear]
)
e verifica se os polígonos
são disjuntos. [Dá para fazer em tempo linear]
- 4.
- Descreva um algoritmo que receba um poliedro convexo no espaço,
através de sua lista de faces, e um ponto p e verifica se esse
ponto está no interior ou exterior desse poliedro.
- 5.
- Considere um poliedro representado por uma estrutura
winged-edge.
a. Escreva um algoritmo que, dada uma face F, obtém todos os vértices desta
face em tempo linear no número de vértices de F.
b. Escreva um algoritmo que, dado um vértice v, obtém todos os vértices
adjacentes a v em tempo linear no número de arestas incidentes a v.
- 6.
- Considere um tetraedro representado pela estrutura winged-edge
como feito em sala de aula, e mostre o resultado de inserir uma aresta ligando
dois vértices já existentes no poliedro (e, portanto, criando uma nova face).
- 7.
- Descreva um algoritmo linear que dada a triangularização de Delaunay
para um conjunto de pontos S, constrói o diagrama de Voronoi para este
conjunto de pontos.
- 8.
- Descreva um conjunto S de n pontos (arbitrário) que não contenha
quatro pontos cocirculares tal que a triangularização de Delaunay tem um
vértice de grau n-1.
- 9.
- Seja S um conjunto de pontos no plano e S1 e S2 uma partição de
S, ou seja,
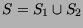 e
e
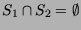 .
Prove que se uv
é um segmento de menor comprimento entre os segmentos que têm uma ponta em
cada conjunto (ou seja,
.
Prove que se uv
é um segmento de menor comprimento entre os segmentos que têm uma ponta em
cada conjunto (ou seja,
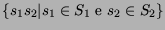 ),
então uv é uma aresta da triangularização de Delaunay.
),
então uv é uma aresta da triangularização de Delaunay.



Next: About this document ...
Carlos Eduardo Ferreira
1999-10-20