Combinatória, Problema dos Caminhos e Caixa de Galton

Leônidas de Oliveira Brandão (DCC - IME - USP)

Resumo

Esta é uma versão digital da apostila sobre o problema dos caminhos/caixas de Galton utilizada em cursos do LEM desde 1996. Nela são abordados vários tópicos (como Triângulo de Pascal e produtos notáveis) e por isso sugerimos ao professor (ou ao leitor interessado) que selecione apenas os itens necessários para o trabalho com sua turma. Destacamos que em 2023 implementamos também um simulador para as caixas de Galton, implementando uma versão digital do dispositivo físico.

1 Objetivos

Esta apostila é dirigida a professores de matemática do Ensino Médio interessados em ensinar Matemática a partir de problemas. O problema central é a Caixa de Galton, estudado por Francis Galton (1822 1911) [1, 2, 3, 4], o qual, para ser resolvido deve ser considerado o problema dos caminhos, envolvendo conceitos básicos de combinatória. A meta principal é despertar o interesse do aluno pela matemática e desenvolver sua capacidade resolver problemas.

Desse modo, apresentamos o assunto de modo construtivo, sugerindo caminhos para que o professor ajude seus alunos na resolução dos problemas a partir de uma metodologia participativa. Como resultado esperamos que o aluno aprenda também o que são e para que servem incógnitas, hipóteses, conjecturas, teoremas, demonstrações e contra-exemplos.

Tópicos Matemáticos discutidos: O que são conjectura, contra-exemplo, demonstração e torema; Combinatória; Triângulo de Pascal; Recorrência; Fatorial; e Caixa de Galton (Francis Galton, 1822-1911).

2 Introdução

Um interessante dispositivo (ilustrado na figura 1) foi proposto por Francis Galton [3], nele bolas são lançadas do topo do dispositivo, contendo fileiras de pinos centrados, sendo que ao bater em um pino tem igual probabilidade de cair em direção ao seu pino imediatamente abaixo pela esquerda ou pela direita. A partir disso Galton observou uma distribuição na forma de sino, com mais bolas caindo nas caixas centrais.

O problema é determinar a probabilidade da bola cair em cada uma das caixas na parte inferior do dispositivo. Entretanto, iniciar por este problema pode ser bastante difícil, então propomos iniciar com sub-problemas que ajudam a resolver o problema das Caixas de Galton [5].

Desse modo, apresentamos inicialmente o problema dos caminhos na seção 3 e discutiremos nas seções 4 e 5, então apresentamos o problemas das Caixas de Galton, mais brevemente, na seção 6, sendo que, para resolvê-lo é necessário saber resolver o primeiro. Com o segundo problema, esperamos exercitar a capacidade de abstração e síntese dos alunos, pois a dificuldade maior está em relacioná-lo com o primeiro.

Na seção 3 daremos uma descrição sucinta do Problema dos Caminhos: em um reticulado, qual o número de caminhos distintos, com distância mínima, entre dois pontos? Na seção 4 discutiremos a metodologia e daremos algumas dicas para quando os alunos não conseguirem avançar na resolução do problema proposto na seção 3. Na seção 5 apresentaremos duas formulações para o problema, abordaremos o princípio multiplicativo e usando-o, proporemos deduções para fórmulas de permutação, de arranjo e de combinação. Na seção 6 apresentaremos o segundo problema (caixa de Galton) e exploraremos outros aspectos importantes no desenvolvimento da matemática. Este problema pode ser assim resumido: em um tabuleiro triangular, com hastes uniformemente distribuídas e aparadores na base, quais as probabilidades de uma bola lançada no topo cair em cada um dos aparadores?

3 Problema

O problema que consideraremos aqui tem a seguinte característica: um enunciado simples e, como veremos na seção 5, envolve vários tópicos matemáticos de segunda grandeza. Resumidamente o problema é: qual o número de caminhos mínimos entre dois pontos num reticulado?

Uma apresentação didática: “Em uma cidade planejada, onde todos os quarteirões são quadrados, e de mesmas dimensões , as ruas numeradas de acordo com um plano cartesiano, de quantas maneiras possíveis podemos ir de uma esquina fixa (origem), até outra esquina qualquer, usando apenas os caminhos mais curtos?”

4 Desenvolvimento da atividade

O professor deve apresentar o problema verbalmente, sem qualquer desenho ou informação extra, dividir a classe em grupos e deixá-los iniciar a busca por soluções. Será tarefa dos alunos encontar uma representação para o problema.

Devido a complexidade do problema, sugerimos que a cada 10 minutos o professor se dirija aos grupos, indagando-os sobre os resultados já obtidos, os quais serão anotados na lousa. O objetivo destas rodadas de divulgação é permitir que a atividade seja mais rápida e que os grupos percebam outras formas de atacar o problema. Após os resultados serem anotados na lousa, pode existir intervalo para discussão, às vezes obrigatório, por exemplo, quando surgirem resultados contraditórios.

O professor poderá fazer algumas observações nos intervalos de discussão, preferencialmente indagações sobre o que já foi obtido ou qual seu significado para a resolução do problema. A seguir apresentamos algumas observações possíveis.

Para que o professor entenda melhor o que estamos propondo nesta atividade, apresentaremos nesta seção uma série de perguntas, respeitando uma “ordem cronológica” na resolução do problema, que o professor poderá utilizar nos momentos em que os alunos se sentirem “perdidos”. Além disto, para seguir de guia ao professor, apresentamos respostas a estas questões.

4.1 Como representar o problema?

Uma etapa muito importante na resolução de problemas é a representação dos mesmos. No caso que estamos considerando, a representação é praticamente a tradução do enunciado, o desenho de um reticulado numerando linha/coluna, como a representação do plano cartesiano. É importante ressaltar a necessidade de numeração linhas/colunas para podermos identificar os diferentes nós (esquinas).

Se os alunos fizeram a representação por meio do desenho acima, ou outro semelhante, parabenize-os: “Vocês acabaram de responder a primeira pergunta quando se tenta resolver um problema.” Se apareceram diferentes numerações (crescente de baixo-esquerda para cima-direita ou o uso de letras, como no jogo batalha naval), é essencial fixar um padrão para que todos “falem a mesma língua”. Sugerimos adotar o padrão acima, por ser o que utilizamos nesta apostila. A questão natural agora é:

4.2 Qual é a esquina origem?

Esta questão não tem uma resposta propriamente dita, mas deve despertar o aluno para a necessidade de se fixar um ponto (esquina) para servir como origem. Por razões de simplicidade, fixe o ponto (0,0).

4.3 Como são os caminhos mínimos (ou mais curtos)?

Pode ser que os alunos não entendam esta questão, neste caso apresente uma alternativa: qual o comprimento de um caminho? É necessário saber distinguí-los e podemos fazer isso contanto o número de nós pelo qual o caminho passa.

Usando a geometria plana, podemos pensar que existem apenas dois tipos de movimentos: para cima/baixo ou para esquerda/direita. Assim podemos enunciar a definição de caminho mínimo contando o número de nós (as "esquinas") pela qual o caminho passa: C é um caminho mínimo entre os pontos/nós A e B <=> qualquer outro caminho de A até B tem tantos ou mais nós que o caminho C.

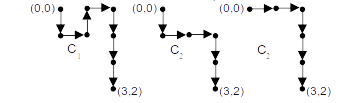
Por exemplo, para um caminho mínimo iniciando em A=(0,0) e finalizando em B, então não deve haver movimento nem para cima e nem para baixo, pois sempre seria possível fazer um sem tais movimentos, reduzindo o tamanho do caminho.

Caminho mínimo a partir de (0,0) não tem movimentos para cima (com em C1) Se o caminho inicia em (0,0), qualquer movimento para cima impede o movimento de ser mínimo, como em C1. Já os caminhos C2 e C3 tem 2 nós a menos.

Caminho mínimo a partir de (0,0) não tem movimentos para esquerda (como em C1) Se o caminho inicia em (0,0), qualquer movimento para esquerda impede o movimento de ser mínimo, como em C1, que tem 7 nós. Já os caminhos C2 e C3 tem 2 nós a menos.

4.4 Quais são os nós (esquinas) até os quais vocês já conhecem o número de caminhos "mais curtos"?

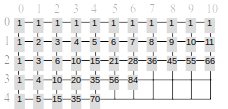
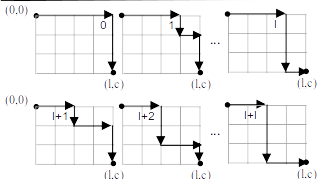
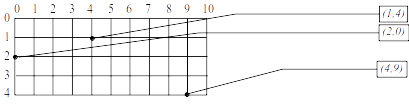
Este é outro ponto inicial na resolução de um problema: resolver na “força bruta” alguns exemplos, sentir a dificuldade e tentar sintetizar propriedades/relações. Os alunos notarão a dificuldade em se calcular o número de caminhos para nós (esquinas) “distantes” da origem A=(0,0) (ambas as componentes, digamos, maiores que 5), como por exemplo, para os pontos B=(4,4) e C=(2,9): total de caminhos até B são 70 e até C são 55 caminhos distintos (vide figura abaixo, na direita).

Nesta etapa podem surgir divergências sobre a quantidades de caminhos distintos até alguns nós (esquinas), principalmente para os pontos “distantes”. Anote em cores diferentes os valores “polêmicos”, para que posteriormente os alunos detectem os valores “corretos”.

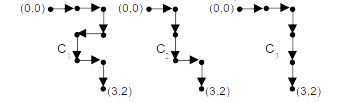
A fim de fixarmos notação denominaremos a tabela abaixo por tabela de caminhos. Sugerimos que use este nome em sua exposição. Para construir tal tabela usamos as propriedades em 4.3, sintetizadas na sequinta propriedade (teorema, que pode ser demonstrado): se C e D são os nós vizinhos de B (respectivamente, acima e esquerda de B), então o total de caminhos de A até B é soma dos caminhos de A até C e de A até D. Isso é ilustrado na figura à esquerda abaixo e na direita, usando tal propriedade construimos o total de caminhos mínimos a partir do nó (0,0).

Todos os caminhos mínimos de A até B (último passo tem que ser via nó C ou nó D)

Tabela com total de caminhos mínimos desde o ponto (0,0), considerando apenas aqueles com menos de 100 possibilidades distintas.

4.5 Qual ou quais são as variáveis deste problema?

Possivelmente os alunos já responderam a esta questão, implicitamente, no ítem anterior. Em geral eles saberão respondê-la mas provavelmente não se preocuparam com a mesma por ser “óbvia”: são os índices de linha coluna do nó (esquina). Como nosso objetivo é desenvolver a capacidade e interesse por pesquisa matemática (mais modestamente, por resolução de problemas matemáticos), é importante fazê-los perceber a relevância da questão, sem a qual não teriam chance sequer de distinguir os pontos.

4.6 Quais são as incógnitas do problema?

Falta aos alunos identificarem exatamente o que procuram responder: determinar os valores da tabela de caminhos. Informalmente isto também já foi respondido no ítem 4.3, porém desejamos “matematizar o problema” (e com isto termos chance de obter mais propriedades), logo é necessário identificar os valores da tabela.

Em outras palavras, estamos em busca de uma função que descreva o número de caminhos (mínimos) para cada par de naturais (nó),

C(m,n) = número de caminhos mais curtos distintos de (0,0) até (m,n)

Comente que neste momento isto pode parecer um detalhe irrelevante, mas pode ajudar em desenvolvimentos futuros. Mais ainda, a situação ideal é obtermos uma expressão fechada para C(m,n), como por exemplo, C(m,n)=m+n ou C(m,n)=mxn (certifique-se que entenderam: se conhecemos a fórmula fechada para calcular C(10,31), por exemplo, basta efetuar uma conta e não um exaustivo trabalho usando o método da “força bruta”, como no item 4.4).

4.7 É coincidência a simetria na reta l = c ?

Se os alunos calcularam corretamente a tabela de caminhos, para um reticulado não muito pequeno, ficará claro uma simetria na reta l = c, ou seja, C(l,c) = C(c,l), para todo par de naturais (l,c).

Se eles sugerirem tal relação merecem seus cumprimentos, pois acabaram de “conjecturar”. É importante dizer-lhes que isto é apenas uma conjectura, ou seja, só se transformará em um teorema após a sua demonstração rigorosa.

Outra possibilidade é procurar por contra-exemplos (explique contra-exemplo a um resultado ou conjectura é um exemplo no qual o resultado ou conjectura não valem, isto é, se mostrem falsos). Qualquer uma destas duas possibilidades é fazer matemática, ressalte isto. A sub-seção seguinte deve ser desenvolvida se alguns alunos acreditarem que a conjectura de 4.7 é falsa.

4.8 Consegue um contra-exemplo?

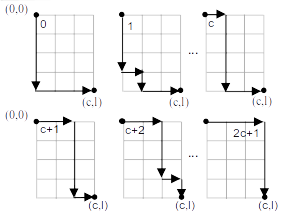
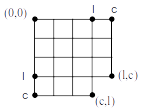
Alguns alunos poderão pensar ter conseguido um contra-exemplo para a simetria em relação à reta l=c, neste caso será necessário fazer na lousa, com calma, para convencê-los que o contra-exemplo não é válido. Se os pontos forem “perto” da origem será fácil verificar o erro. Se estes pontos, (l,c) e (c,l), forem distantes da origem (l ou c “grandes”), a tarefa de encontrar o erro será difícil. Tente sistematiziar a contagem, como no gráfico a seguir, fazendo:

• no caso de (l,c): avançar a contagem da esquerda para a direita, após uma linha inteira avançando para seguinte
• no caso de (c,l): avançar a contagem de cima para baixo, após uma coluna inteira avançando para a seguinte.

A contagem de modo sistemático é ilustrado nas figuras a seguir, estando do lado esquerdo a contagem de (0,0) até o nó (l,c) e do lado direito, os caminhos distintos desde (0,0) até o nó (c,l)

Contagem sistemática de (0,0) para (l,c)

Contagem sistemática de (0,0) para (c,l)

Uma vez entendido o processo de contagem, sugira aos alunos contabilizarem construindo a tabela ao lado. É importante perceber que o número de caminhos de (0,0) até (l,c), será o mesmo que o número de caminhos de (0,0) até (c,l), com em 4.9.

Durante o processo de contagem para exemplos grandes, é possível que os alunos percebam alguma outra propriedade, como a indicada no item 4.10, ou que percebam intuitivamente a validade da conjectura.

4.9 Como provar a simetria?

Inicialmente, apresente o argumento de contagem do item anterior. Assim os alunos “acreditarão” na validade da conjectura. Não avance muito na formalização desta demonstração, pois para fazer isto seria necessário apresentar outros resultados, como os explorados nas seções 5.1 e 5.2.

Utilize o seguinte raciocíonio (sempre usando gráficos):
· considere um caminho qualquer até (l,c) (ou até (c,l)), diremos que o “inverso” deste caminho é aquele com igual número de passos, porém invertendo os passos para direita por passos para baixo e vice-versa;
· um caminho tem um e só um “inverso”;
· se S1 é o conjunto de caminhos até (l,c) e S2 até (c,l), para todo caminho de S1 existe um “inverso” em S2 e do mesmo modo, todo caminho de S2 tem um correspondente em S1, logo #S1 = #S2 (use os gráficos anteriores para justificar).

Nota: usamos o símbolo # para indicar a cardinalidade de conjuntos finitos enumeráveis (basicamente, subconjuntos finitos dos naturais). Por exemplo: #{0,1,2}=3; #{20,12.2}=2; #{a,b,e,2,4}=5; #{♠,♥,♣,♦}=4; e #{α,β,γ,δ,ε,ζ,θ}=7.

4.10 C(m,n) = C(m-1,n) + C(m,n-1) sempre?

Durante as tentativas de busca por resposta para os ítens anteriores, principalmente durante a montagem da tabela, é possível que algum aluno perceba a ocorrência da relação (recorrente) C(m,n)=C(m-1,n)+C(m,n-1), e postule esta importante conjectura. Se algum grupo a propôs chame a atenção da classe para esta sensacional descoberta: uma incrível relação (no caso de a provarem posteriormente) ou, ao menos, uma incrível coincidência (no caso de posteriormente apresentarem um contra-exemplo).

Deixe-os pensar bastante a respeito, tentando provar ou apresentar contra-exemplo. A demonstração desta conjectura é simples, como vemos a seguir.

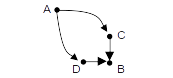
Teorema 1 Para todo par (m,n)¹(0,0), C(m,n)=C(m-1,n)+C(m,n-1). Demonstração Como discutido na seção 4.3, se o caminho é mínimo então não pode haver passos para trás ou para cima, para cada par (m,n), só existem dois tipos de caminhos até (m,n), aqueles que passam pelo vizinho superior de (m,n), o nó (m-1,n), e aqueles que passam pelo vizinho à esquerda de (m,n), o nó (m,n-1). Seja C1 um caminho do primeiro tipo e C2 do segundo:

C1 = Conjuntos dos caminhos mínimos de (0,0) até (m-1,n) e C2 = Conjuntos dos caminhos mínimos de (0,0) até (m1,n-1).

Logo, C(m,n) = #C1 + #C2 ,

mas, por definição de C(m-1,n) e de C(m,n-1), #C1 + #C2 = C(m-1,n) +C(m,n-1), completando a demonstração.

5 Formulação

As respostas às questões 4.9 e 4.10 permitem dois tipos distintos e complementares de demonstrações que apresentaremos nas próximas sub-seções. Usaremos a seguinte notação:
  b = representará um movimento para baixo;
  f = representará um movimento para direita.

5.1 Relação recorrente

Na sub-seção 4.10, foi deduzida a relação recorrente (no lado direito da definição da função aparece ele mesma, como a função fatorial: f(n) = nxf(n-1), se n>0 ou f(n) = 1, se n=0), C(m,n) = C(m-1,n) + C(m,n-1). Funções recorrentes têm uma desvantagem prática, para computar a função em um ponto qualquer necessitamos computá-la para vários outros pontos.

Se a escola dispõe de alguns microcomputadores e de um programa como o Pari-GP (https://pari.math.u-bordeaux.fr) ou Octave (https://octave.org), ambos gratuitos, seria muito interessante que o professor desafiasse os alunos para que eles calculem a tabela de caminhos, para um (m,n) grande, usando esses programas ou outro semelhante.

Veremos na sub-seção 5.3, como encontrar uma forma fechada para C(m,n) e que a tabela de movimento está relacionada com o Triângulo de Pascal.

5.2 Relação derivada da simetria

Na tentativa de demonstrar esta simetria, talvez os alunos percebam a seguinte relação, que deve ser exposta pelo professor para servir como exemplo. Alguns alunos podem argumentar que tal resultado não necessitaria de uma demonstração: explique que algumas vezes a intuição engana, uma demonstração serviria para evitar estes enganos.

Lema 1. Qualquer que seja o caminho até (m,n), o número de passos para baixo e para direita são sempre os mesmos.
Demostração. A cada passo uma das componentes é acrescida de uma unidade. Como não existe passo que decresça a primeira ou segunda componentes, de (0,0) até (m,n) precisamos de exatamente m passos para baixo e n para direita, completando a demonstração. O lema 1 é ilustrado na figura abaixo: os 3 caminhos apresentados, todos eles, tem 2 passos para baixo e 4 passos para a direita.

Uma vez demonstrado o lema acima (o nome lema é utilizado normalmente para resultados não definitivos, ou seja, que servem para demonstrar outros resultados), fica mais fácil responder a questão da simetria (tente fazer a demonstração abaixo requerendo sugestões dos alunos).

Teorema 2. C(m,n) = C(n,m), para quaisquer m e n naturais.
Demostração. Sendo Cx,y o conjunto dos caminhos de (0,0) até (x,y), do lema anterior sabemos que o número m de passos para baixo em qualquer caminho de C_m,n é igual ao número de passos para direita em qualquer caminho de Cn,m. O mesmo vale para os passos a baixo de Cn,m e à direita de C_m,n. Logo, se c∈C_m,n e D é o “caminho inverso de c”, construído a partir de c, trocando os passos para baixo por passos à direita e vice-versa, então D∈Cn,m . Do mesmo modo, se c∈Cn,m e D é o inverso de c, então D∈C_m,n. Portanto, a cardinalidade de C_m,n é igual à de Cn,m (#C_m,n =#C_n,m), completando a demonstração.

A próxima sub-seção talvez seja a mais difícil, pois nela apresentaremos uma para a forma fechada (não recorrente) de C_m,n. Cabe ao professor decidir se usará esta dedução com seus alunos (para este “exercício” não se estender muito mais, sugerimos que o professor apenas a apresente, sem muita participação dos alunos).

5.3 Fórmula fechada para C(m,n)

Já temos dois resultados importantes: no primeiro uma fórmula recorrente (4.10) e no segundo uma propriedade aparentemente não aproveitada (4.7, 4.8 e 4.9).

Nesta sub-seção usaremos estes dois resultados para obter uma fórmula fechada para C(m,n). Se os alunos não obtiverem estes resultados, sugerimos que o professor apresente os mesmos com cuidado, tentando fazer com que os alunos participem desta demonstração. Se os alunos já tiverem conseguido os resultados, caberá ao professor, eventualmente, sistematizá-los de modo que toda a classe compreenda o processo de dedução.

Etapa 1: O problema de decisão

Com a finalidade de tornar a demonstração mais “suave”, consideremos um problema equivalente, que chamaremos de problema de decisão. Em um caminho para (m,n) teremos que tomar m+n decisões (lema anterior): a cada esquina decidimos ir para baixo ou para direita. Portanto um problema equivalente à determinação do número de caminhos distintos até (m,n) é o problema de decisão: para chegarmos até (m,n) qual o tamanho (cardinalidade) do conjunto de decisões (m+n decisões) que podemos tomar?

Etapa 2: Decisões para direita definem o caminho

No caminho para (m,n), m+n decisões serão tomadas sendo que n delas deverão ser para direita. Assim, se alguém contar onde foram tomadas as decisões para direita (d) o caminho estará definido, como ilustrado abaixo.

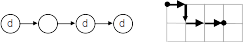
Portanto, podemos novamente mudar o enunciado de nosso problema para a seguinte forma equivalente: determinar quantos são os caminhos distintos para k decisões, onde n delas devem ser para direita (k=m+n).

Etapa 3: Fundamentos

A fim de ilustrar o tipo de problema que temos, o professor pode definir o Princípio Multiplicativo: Sejam A e B eventos distintos. Se A pode produzir m diferentes “valores” e B n “valores”, então o evento (AB) pode produzir m x n valores diferentes.

Exemplo: Apresente o número de diferentes senhas bancárias usando apenas 3 dígitos.
Os eventos são: A1 (primeiro dígito), A2 (segundo dígito) e A3 (terceiro).

Possibilidades são: #A1 x #A2 x #A3 = 10 x 10 x 10 = 103.

No exemplo acima, para se obter o total de eventos existentes, usa-se a propriedade multiplicativa: se dois eventos A e B são independentes (o que ocorre em um não pode alterar o outro), então o número total de eventos (A,B) é #A x #B. E se os eventos não forem independentes, o que muda ?

Para seus alunos entederem estes cálculos de número de eventos, proponha-lhes o seguinte problema:

Exercício: Se você dispõe de 4 diferentes caminhos, cada um em uma das 4 direções cardeais, quantos são os diferentes caminhos que pode seguir ?
Solução: (Deixe os tentarem, depois formalize na lousa o que conseguiram, intervindo quando necessário.)

Seja d1, d2, d3 e d4, a representação dos caminhos (poderia ser N, S, L e O, mas usaremos algo parecido com a primeira representação, assim dê preferência a ela). Sejam A1, A2, A3 e A4 os instantes em que se decide a direção a ser tomada .

Portanto, podemos novamente mudar o enunciado de nosso problema para a seguinte forma equivalente: determinar quantos são os caminhos distintos para k decisões, onde n delas devem ser para direita (k=m+n).

Etapa 3: Fundamentos

A fim de ilustrar o tipo de problema que temos, o professor pode definir o Princípio Multiplicativo: Sejam A e B eventos distintos. Se A pode produzir m diferentes “valores” e B n “valores”, então o evento (AB) pode produzir m x n valores diferentes.

Exemplo: Apresente o número de diferentes senhas bancárias usando apenas 3 dígitos.
Os eventos são: A1 (primeiro dígito), A2 (segundo dígito) e A3 (terceiro).

Possibilidades são: #A1 x #A2 x #A3 = 10 x 10 x 10 = 103.

No exemplo acima, para se obter o total de eventos existentes, usa-se a propriedade multiplicativa: se dois eventos A e B são independentes (o que ocorre em um não pode alterar o outro), então o número total de eventos (A,B) é #A x #B. E se os eventos não forem independentes, o que muda ?

Para seus alunos entederem estes cálculos de número de eventos, proponha-lhes o seguinte problema:

Exercício: Se você dispõe de 4 diferentes caminhos, cada um em uma das 4 direções cardeais, quantos são os diferentes caminhos que pode seguir ?
Solução: (Deixe os tentarem, depois formalize na lousa o que conseguiram, intervindo quando necessário.)

Seja d1, d2, d3 e d4, a representação dos caminhos (poderia ser N, S, L e O, mas usaremos algo parecido com a primeira representação, assim dê preferência a ela).
Sejam A1, A2, A3 e A4 os instantes em que se decide a direção a ser tomada .

A1 : No início do caminho nenhuma direção ainda foi usada, logo podemos usar cada uma delas, resultando em 4 possibilidades, ou seja, #A1=4. A2 : No segundo passo dispomos de 3 direções, uma vez que uma já foi usada no passo 1, logo #A2=3. A3 : No terceiro passo dispomos de 2 direções ainda não usadas, assim, #A3=3. A4 : No último passo não resta opção além de uma restante, assim, #A4=1.

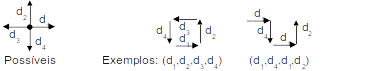
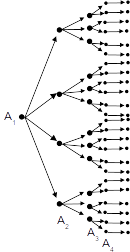
Logo, o número total de caminhos possíveis é

#A1 x #A2 x #A3 x #A3 = 4 x 3 x 2 x 1 = 4 ! = 24.

O que acaba de ser explorado é o conceito de permutação: é possível listar n elementos distintos, de n!=nx (n-1) x... x 2 x 1 maneiras distintas.

Etapa 4: O Problema dos Caminhos e Arranjos

À luz dos resultados explorados, o que podemos fazer a respeito de nosso problema de distribuição das direções à direita? Ou seja, qual o total de caminhos distintos para chegar ao nó/ponto (m,n)?

Dispomos de k=m+n decisões (frente ou direita). Em exatamente n delas devemos nos dirigir para a direita.

Denotaremos as direções por f1, f2 até fn, cada fi deveria ser d=direita ou f=frente, mas para o raciocínio inicial pensaremos que cada uma pode ser diferente umas das outras. Vamos contar de quantas maneiras diferentes podemos listá-las (ordem das decisões). Usando a represenção gráfica abaixo, com caixas 1 até k, contaremos o número de diferentes listas que podemos produzir “jogando” as direções f1 até fn nas k caixas, nessa sequência.

Assim, para

f1 dispomos de k posições	qualquer uma das k esquinas do caminho (esquinas ocupadas: 0)
f2 dispomos de k-1 posições	qualquer das k esquinas, excetuando-se aquela que f1 já “ocupa”
f3 dispomos de k-2 posições	todas as esquinas, excetuando-se as já ocupadas por f1 e f2
· · ·	· · ·
fn-1 dispomos de k-(n-2)	até aqui já estão ocupadas n-2 esquinas
fn dispomos de k-(n-1)	já temos n-1 esquinas ocupadas, portanto restam apenas k-(n-1)

Portanto, usando o princípio multiplicativo, temos k x (k-1) x ... x (k-n+2) x (k-n+1), que pode ser colocado em uma forma matemática mais sucinta, multiplicando-se por (k-n)! e dividindo pelo mesmo fator, assim obtemos

k x (k-1) x... x (k-n+2)x (k-n+1)x (k-n)! / (k-n)! = k! / (k-n)!.

Acabamos de computar o número de arranjos possíveis com k elementos, tomados em grupos de n (n≤k): podemos listar

Etapa 5: O Problema dos Caminhos e Combinações

O que obtivemos na etapa anterior ainda não é a forma (final) que procuramos. Indague aos alunos: Por que ?
Ainda não deve ser explorado com eles o conceito de combinação, mas basicamente, a resposta a esta pergunta é a essência da diferença entre arranjo e combinação: arranjos fornecem a quantidade de listas diferentes, nas quais a ordem é importante, em nosso problema a ordem não importa. Vamos exemplificar para k=n=2. Na fórmula anterior, A2,2 resultaria 2: { (f1,f2), (f2,f1) }.

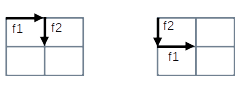
No entanto, em nosso problema ambos os caminhos levariam ao mesmo ponto, ou seja, a ordem das direções é irrelevante. Isso está ilustrado na imagem. Portanto, estamos interessados em contar não quantas listas diferentes podemos formar com k elementos tomados n a n, mas sim em contar a quantidade de diferentes conjuntos que podemos formar com k elementos tomados n a n.

Vejamos como podemos computar o número desejado a partir do que já conseguimos:

• Vamos agrupar (particionar) as listas de acordo com as posições ocupadas pelas decisões ir para a direita em conjuntos {Ai}i. Assim, por exemplo, para o caso k=5 e n=3, as listas (-,f1,-,f2,f3), (-,f1,-,f3,f2), (-,f2,-,f1,f3), (-,f2,-,f3,f1), (-,f3,-,f1,f2) e (-,f3,-,f2,f1) dariam origem a um conjunto com 3! elementos.
• Quantos elementos tem cada conjunto Ai? Em um vetor com k posições, n delas serão ocupadas pelos {f1, f2, ... , fn}, assim Ai tem n! elementos (vide etapa 3).
• Suponhamos que neste processo surjam a conjuntos Ai, desde A1 até Aa, então a fórmula final é

Após os alunos entenderem o exposto acima, formalize. Acabamos de discutir combinação simples: em um conjunto de k elementos é possível formar C_k,n conjuntos distintos, cada um destes com n elementos. Outra notação para combinação simples é

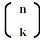
Resumo:
· Uma palavra que caracteriza arranjo é lista, pois em arranjos a ordem importa;
· A palavra que caracteriza combinação é conjunto, pois neste caso a ordem é irrelevante; e
· Permutação é um caso particular de arranjo, pois permutação é uma lista, só que tomando-se todos os elementos.

Etapa 6: Verificação dos Resultados

Nesta etapa apresentamos o seguinte desafio (a ser feito aos estudantes): Muito bem, parece que resolvemos o problema, mas será que não erramos em algum lugar? Será que o que fizemos é coerente com os resultados iniciais? A fórmula obtida produz a mesma tabela de caminhos?

Comente com seus alunos que esta é uma etapa comum na pesquisa: verificação dos resultados obtidos. Portanto não serviria como demonstração dos resultados mas apenas um teste.

· C(m,n) = C_m+n,n (Triângulo de Pascal)

Lembrando que o número de caminhos até a esquina (m,n), em nossa notação inicial, é C(m,n) e na notação de combinação simples é C_k,n, onde k=m+n (isto é resultado da etapa 2). Faça com os alunos os cálculos para as esquinas computadas na tabela de caminhos. Isto deverá ser igual, caso contrário, peça aos alunos para identificarem onde está o erro. Lembre-os da convenção (ou defina) 0!=1.

Comente que estas tabelas são muito conhecidas, em uma forma ligeiramente diferente, ela é conhecida como Triângulo de Pascal. Nos gráficos acima, o Triângulo de Pascal é obtido de “nossa tabela” através das diagonais (vide setas).

· C_k,n = C_k-1,n + C_k-1,n-1 (Relação de Stifel)

Para demonstrarmos a validade da relação de Stifel, basta fazermos algumas contas, como indicado abaixo (ou usando o resultado C(m,n)=C_m+n,n e o teorema 1, na página 6, segue o resultado)

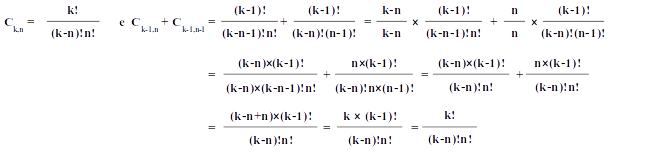
Note que usamos o truque de multiplicar e dividir por um mesmo valor duas vezes (por k-n e por n) e depois usamos a definição de fatorial para simplificar ((k-n)×(k-n-1)! = (k-n)!; n×(n-1)! = n!; e k×(k-1)! = k!).

Argumento direto de porque vale a relação de Stiefel: (sugerimos um caso concreto para explicar aos alunos) Seja S um conjunto com n elementos distintos, contendo a letra α. Defina por Sn,k o conjunto de todos os subconjuntos de S com k elementos distintos. Podemos particionar Sn,k em dois conjuntos complementares (com interseção vazia e união formando Sn,k)

• S1 = {todos subconjuntos de Sn,k, onde não aparece α}
• S2 = {todos subconjuntos de Sn,k, onde aparece α}

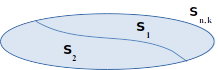
Devemos notar que (abaixo o símbolo \ significa menos aplicado à conjuntos: A\B = conjunto dos elementos de A que não estão em B):

• #S1 = C_n-1,k, pois tomamos todos os subconjuntos com k elementos distintos de S que não contém o elemento α, logo tomamos todas as combinações de n-1 elementos de S \{α}, k-a-k;
• #S2 = C_n-1,k-1, pois tomamos todos os subconjuntos de S\{α}, k-1 a k-1, anexando-se sempre o α.

Logo,

Cn,k = #Sn,k = #S1 + #S2= C_n-1,k + C_n-1,k-1.

Etapa 7: Uma aplicação para o Triângulo de Pascal (fórmula do binômio de Newton3)

Os coeficientes do produto notável (a+b)n , com a¹0 e b¹0, é o n-ésima linha do Triângulo de Pascal.

(a+b)⁰ = 1
(a+b)¹ = 1 a¹ b⁰ + 1 a⁰ b¹
(a+b)² = 1 a² b⁰ + 2 a¹ b¹ + 1 a⁰ b²
(a+b)³ = 1 a³ b⁰ + 3 a² b¹ + 3 a¹ b²+ 1 a⁰ b³
em geral,
(a+b)ⁿ = C_n,0 aⁿ b⁰ + C_n,1 a^n-1 b¹ + C_n,2 a^n-2 b²+ . . . + C_n,n a⁰ bⁿ.

Porque vale a última relação? (pode-se usar este exemplo para ilustrar a demonstração do item anterior)
Seja

(a+b)ⁿ = C(n,0) aⁿ b⁰ + C(n-1,1) a^n-1 b¹ +...+ C(n-(n-1),n-1) a¹ b^n-1 + C(0,n) a⁰ bⁿ.
Vamos identificar as posições p1, p2, ... , pn dos termos (a+b), como indicado na figura abaixo. Portanto em cada posição ou aparece a ou aparece b.

Assim, C(n-i,i) equivale ao número de diferentes posições (dentre p1,...,pn) para n-i letras a’s (ou, i letras b’s). Logo,

Ao apresentar esta demonstração seja cuidadoso, principalmente no argumento de que está transformando o problema inicial (binômio) em outro mais “simples”: contar como distribuir n-i letras a’s (e consequentemente, i letras b’s) em n compartimentos, pois no binômio, cada um dos n termos contribui com exatamente uma letra e como estamos interessados em contar o número de parcelas an-i bi, devemos computar todas as combinações (sequências) formadas n-i letras a’s (ou equivalentemente, como pode ser percebido na equação acima, i letras b’s - sobre esta equivalência vide raciocínio análogo ao final da seção 6).

6 Mais um problema: Caixa de Galton

Nesta seção vamos propor um outro problema a ser desenvolvido com os alunos, nos mesmos moldes do anterior. Uma vez resolvido o problema anterior, este será muito mais simples. Nele, o que estaremos exercitando mais é a capacidade do aluno de abstrair ou relacionar conceitos. Seria interessante que este fosse desenvolvido, digamos, na semana seguinte ao término do anterior.

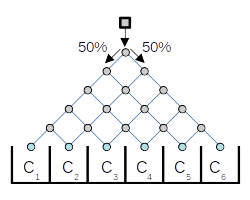
Problema: Considerando o tabuleiro ao lado, no qual lançamos uma bola na posição 0 (topo) e que, após bater em um pino (os círculos cinzas), segue para esquerda ou para a direita com igual probabilidade (50%).

Após lançar a bola um número grande de vezes, em média, quantas bolas cairão em cada caixas (C1, C2, C3, C4, C5, C6 e C7) ?

Deixe os alunos trabalhar em grupo, após algum tempo coloque na lousa o que conseguiram e junto com a classe complete a demonstração. A seguir uma sugestão de apresentação.

Solução: O cálculo de média deve levar em consideração um número grande lançamentos, e estes números refletem, aproximadamente, as probabilidades. Esta é a lei dos grandes números: a frequência se aproxima da probabilidade (se tiver dúvidas verifique em qualquer texto introdutório de Estatística). Dê um exemplo simples: se você jogar uma moeda, não viciada, 100 vezes, aproximadamente 50 dos lançamentos resultarão cara e 50 coroa.

Deste modo, devemos calcular a probabilidade da bola cair em cada uma das caixas. Para uma breve recordação (ou introdução) do conceito de probabilidade: No caso discreto (os eventos são enumeráveis), seja A o conjunto total dos eventos e B ⊆ A o conjunto que chamamos de favoráveis.
Se cada elemento de A é equiprovável (mesma probabilidade de ser sorteado),

Pr[selecionar um elemento de B] = #B/#A = (número de eventos favoráveis) / (número total de eventos)
Portanto, o mais difícil neste problema é: determinar como contar o número de eventos. Se algum aluno conseguir identificar isto, ele merece elogios, pois resolveu a parte mais complicada do problema (supondo já saberem o Problema dos Caminhos).

Para podermos contar o número de eventos precisamos inicialmente caracterizar estes eventos. Sempre que uma bola atinge uma haste, ela vai para a direita (d) ou para a esquerda (e), assim para que uma bola caia em uma determinada caixa, digamos Ci é necessário a ocorrência de uma sequência de e e d´s tais que resulte na posição da caixa Ci. Por exemplo, para a bola cair na caixa C7 só existe uma possibilidade, (d,d,d,d,d,d), já a caixa C2 tem seis caminhos, a saber, (d,e,e,e,e,e), (e,d,e,e,e,e), (e,e,d,e,e,e), (e,e,e,d,e,e), (e,e,e,e,d,e), (e,e,e,e,e,d).

Portanto, a resposta à questão acima é:

#{bola cair na caixa Ci} = número de caminhos distintos de 0 até Ci.

Se os alunos não conseguiram chegar sozinhos nesta caracterização, após esta ser exposta, eles deverão perceber a relação com o problema anterior. Usando a notação do exercício anterior,

C1=C(6,0)   |   C2=C(5,1)   |   C3=C(4,2)   |   C4=C(3,3)   |   C5=C(2,4)   |   C6=C(1,5)   |   C7=C(0,6)

Logo, considerando T= C(6,0) + C(5,1) + C(4,2) + C(3,3) + C(2,4) + C(1,5) + C(0,6), temos

Pr[bola cair na caixa (m,n)] = C(m,n)/T = C_m+n,n / T

E se desejarmos, também um caso geral para este problema, isto é, o tabuleiro não é mais fixo com 6 fileiras de hastes, mas arbitrário K? O mais difícil aqui é computar T, que neste caso seria

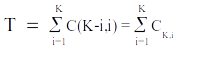
Parece difícil calcular este valor. Na verdade, nesta forma, é muito difícil computar T. No entanto utilizando outro raciocínio é possível obter este “rapidamente” resultado (comente que em Matemática isto ocorre com frequência: um problema aparentemente difícil pode ser facilmente resolvido se utilizarmos o “caminho” / “ferramenta” adequados).

Basicamente o que desejamos é: computar todos os possíveis caminhos (utilizando d e e) de comprimento K.

Portanto, podemos mais uma vez pensar em decisões: um caminho qualquer é formado por K decisões, onde cada uma delas ou é para a direita (d) ou é a esquerda (e).

Assim, o número total de caminhos é igual ao número de sequências de comprimento K (K letras), formadas pelas letras {d, e} e utilizando o princípio multiplicativo, obtemos que

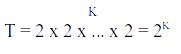
ou seja,

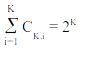
e

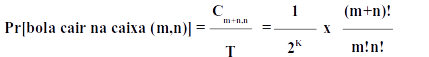
7 Referências bibliográfica

• [1] História da Matemática, Carl B. Boyer (trad. profa. Elza F. Gomide), Ed. Edgard Blucher, 1974.
• [2] The MacTutor History of Mathematics archive, URL: https://mathshistory.st-andrews.ac.uk/HistTopics/, última consulta em 01/03/2023.
• [3] The MacTutor History of Mathematics archive, URL: https://mathshistory.st-andrews.ac.uk/Biographies/Galton/, última consulta em 01/03/2023.
• [4] Sir Francis Galton (16 February 1822 - 17 January 1911), URL: https://en.wikipedia.org/wiki/Francis_Galton, última consulta em 01/03/2023.
• [5] iGalton: simulador para o problema das Caixas de Galton, URL: https://www.matematica.br/igalton, última consulta em 01/03/2023.