Código de correção - código de Hamming

Num código de deteção, como paridade, o erro de 1 bit é detectado. Mas não se sabe onde está o erro, ou seja, qual o bit errado. O dado precisa ser lido (ou retransmitido, no caso de comunicação de dados) de novo.

Num código de correção, sabe-se onde está o erro, de modo que é possível corrigi-lo.

Vejamos o código de Hamming para dados de 4 bits. Vamos acrescentar nesse caso mais 3 bits adicionais. Primeiro um exemplo.

Seja o dado 1101. Para obter os 3 bits extras, vamos inicialmente encarar 1101 como os bits nas regiões de interseção $AB, AC, BC, ABC$, onde $A, B, C$ são diagramas de Venn.

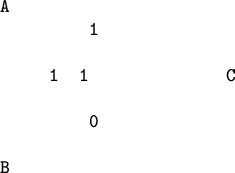
Agora vamos acrescentar um bit de paridade em cada uma das 3 regiões vazias acima para dar paridade par em $A, B$, e $C$.

Erro de 1 bit (qualquer um dos 7 bits) pode ser localizado.

Tal erro pode ser detectado de modo simples, como se segue:

• região $A$: paridade errada

• região $B$: paridade OK

• região $C$: paridade errada

• Conclusão: regiao $AC$ errada. Logo o bit daquela região devia ser 1.

Agora vamos rever o método:

Sejam os $n$ (igual a 4) bits do dado original

$$m_1 m_2 m_3 m_4 = 1101$$

Vamos acrescentar $k$ (igual a 3) bits extras e produzimos o seguinte código de $n+k$ (igual a 7) bits

$x_{1} = m_{1} \oplus m_{2} \oplus m_{4}$	1
$x_{2} = m_{1} \oplus m_{3} \oplus m_{4}$	0
$x_{3} = m_{1}$	1
$x_{4} = m_{2} \oplus m_{3} \oplus m_{4}$	0
$x_{5} = m_{2}$	1
$x_{6} = m_{3}$	0
$x_{7} = m_{4}$	1

Ao ler a memória desses 7 bits, suponhamos o seguinte resultado de leitura (com erro de 1 bit):

$$\begin{eqnarray*} y_{1} & = & 1 \\ y_{2} & = & 0 \\ y_{3} & = & 1 \\ y_{4... ...{ (erro: devia ser 1)} \\ y_{6} & = & 0 \\ y_{7} & = & 1 \\ \end{eqnarray*}$$

Calculamos os valores $k_{3} k_{2} k_{1}$:

$k_{3} = y_{4} \oplus y_{5} \oplus y_{6} \oplus y_{7}$	1
$k_{2} = y_{2} \oplus y_{3} \oplus y_{6} \oplus y_{7}$	0
$k_{1} = y_{1} \oplus y_{3} \oplus y_{5} \oplus y_{7}$	1

Temos $k_{3} k_{2} k_{1} = 101.$

Se $k_{3} k_{2} k_{1} = 000$ então não há erro. Caso contrário, $k_{3} k_{2} k_{1}$ fornecerá o valor binário de $j$ do bit errado $y_{j}$.

No nosso caso, $k_{3} k_{2} k_{1} = 101$ indica que $y_{5}$ está errado. Logo, $y_{5}$ deve ser 1 ao invés de 0.

A tabela baixo mostra o número de bits adicionais para vários tamanhos de palavras:

Palavra	Extras	Total	``overhead''
$n$ bits	$k$ bits
8	4	12	50 %
16	5	21	31
32	6	38	19
64	7	71	11
128	8	136	6
256	9	265	4