Algoritmo de Ford-Fulkerson para fluxo máximo num grafo

Um pseudocaminho num grafo é uma sequência de vértices dotada da seguinte propriedade: para cada par v w de vértices consecutivos,

No primeiro caso, dizemos que v–w é um arco direto (= forward arc) do pseudocaminho. No segundo caso, dizemos que w–v é um arco reverso (= backward arc) do pseudocaminho. Um pseudocaminho sem arcos reversos é um caminho.

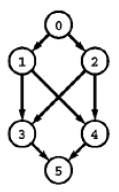
Exemplo A. Considere o grafo definido pelo conjunto de arcos 0-1 0-2 1-3 1-4 2-3 2-4 3-5 4-5. A sequência de vértices 0 2 3 1 4 5 é um pseudocaminho. Ele pode ser indicado assim:

Pseudocaminhos aumentadores

Suponha dado um grafo capacitado e um fluxo que respeita as capacidades dos arcos. Dizemos que um arco v–w está cheio se o fluxo no arco é igual à capacidade do arco. Dizemos que um arco v–w está vazio se o fluxo no arco é nulo.

Em relação a esse fluxo, um pseudocaminho é aumentador (= augmenting) se vai do vértice inicial ao final do grafo e tem as seguintes propriedades:

Dado um pseudocaminho aumentador relativo a um fluxo f, a operação de enviar ε unidades de fluxo ao longo do pseudocaminho consiste em calcular um novo fluxo da seguinte maneira:

É fácil verificar que o resultado dessa operação é um fluxo. Ademais, a operação acrescenta ε à intensidade do fluxo. A operação de envio de ε unidades de fluxo ao longo de um pseudocaminho aumentador é análoga à operação M⊕P usada para aumentar um emprelhamento num grafo não-dirigido bipartido.

Exemplo B. Considere o grafo capacitado definido pela tabela abaixo (o mesmo do exemplo A). A segunda linha da tabela dá as capacidades dos arcos e a terceira define um fluxo (com - no lugar de 0). O vértice inicial é 0 e o final é 5.

A sequência 0-2-3=1-4-5 é um pseudocaminho aumentador. Se enviarmos 10 unidades de fluxo ao longo desse pseudocaminho, teremos um novo fluxo:

Exercícios 1

Mostre que o envio de ε unidades de fluxo ao longo de um pseudocaminho aumentador produz um novo fluxo.

Capacidade residual de um pseudocaminho

Suponha dado um grafo capacitado com vértice inicial e vértice final. Seja f um fluxo no grafo que respeita a capacidade c. Suponha dado um pseudocaminho aumentador relativo a f. A capacidade residual de um arco direto v–w do pseudocaminho é a diferença

sendo c_vw a capacidade e f_vw o fluxo no arco v–w. A capacidade residual de um arco reverso w–v do pseudocaminho é

A capacidade residual do pseudocaminho todo é a menor das capacidades residuais dos seus arcos. É claro que a capacidade residual de um pseudocaminho aumentador é estritamente positiva.

Digamos que δ é a capacidade residual de um pseudocaminho aumentador P e ε é um número entre 0 e δ. Se enviarmos ε unidades de fluxo ao longo de P, produziremos um novo fluxo que respeita as capacidades dos arcos. A intensidade do novo fluxo será ε unidades maior que a intensidade do fluxo original.

Exemplo C. Considere o grafo capacitado definido pela tabela (o mesmo dos exemplos A e B). O vértice inicial é 0 e o final é 5. A segunda linha da tabela dá as capacidades dos arcos e a terceira define um fluxo.

As capacidades residuais dos arcos do pseudocaminho aumentador 0-2-3=1-4-5 estão indicadas a seguir:

Exercícios 2

★ Considere o grafo capacitado definido pela tabela abaixo, com as capacidades dadas na segunda linha da tabela. Seja 0 o vértice inicial e 3 o vértice final. O fluxo dado na terceira linha respeita as capacidades? Qual a intensidade desse fluxo? Calcule a capacidade residual do pseudocaminho aumentador 0-2=1-3. Use o pseudocaminho para encontrar um novo fluxo. Qual a intensidade do novo fluxo?
```
0-1 0-2 1-2 1-3 2-3 
 20  20  20  20  20
 20   -  20   -  20 
```

O algoritmo de Ford-Fulkerson

O algoritmo de Ford-Fulkerson, também conhecido como algoritmo dos pseudocaminhos aumentadores, resolve o problema do fluxo máximo. [!]

Cada iteração começa com um fluxo f que respeita as capacidades dos arcos. A primeira iteração começa com o fluxo nulo. O processo iterativo consiste no seguinte: enquanto existe pseudocaminho aumentador,

Por incrível que pareça, esse simples algoritmo produz um fluxo de intensidade máxima! A prova desse fato, será discutida na próximo capítulo, depois que tivermos introduzido o conceito de capacidade de um corte.

Eis uma propriedade importante do algoritmo: se as capacidades dos arcos são números inteiros, o fluxo em cada arco também permanecerá inteiro ao longo da execução do algoritmo.

Exemplo D. Calculemos um fluxo máximo no grafo capacitado descrito a seguir tomando 0 como vértice inicial e 5 como vértice final.

Comece com fluxo nulo. Considere o pseudocaminho aumentador 0-1-3-5 , que tem capacidade residual 20. Envie 20 unidades de fluxo ao longo do pseudocaminho para obter um segundo fluxo:

Agora considere o pseudocaminho aumentador 0-2-4-5 relativo ao segundo fluxo. Esse pseudocaminho tem capacidade residual 10. Envie 10 unidades de fluxo ao longo desse pseudocaminho para obter um terceiro fluxo:

Agora considere o pseudocaminho aumentador 0-2-3=1-4-5 relativo ao terceiro fluxo. Esse pseudocaminho tem capacidade residual 10. Envie 10 unidades de fluxo ao longo desse pseudocaminho para obter um quarto fluxo:

Exemplo E. Veja outra sequência de pseudocaminhos aumentadores (coluna direita da tabela abaixo) para o grafo capacitado do exemplo D. Cada um dos pseudocaminhos aumentadores tem capacidade residual 10. A sequência transforma um fluxo inicial de intensidade 0 em um fluxo final de intensidade 40 (parte esquerda da tabela):

Note que todos os fluxos da sequência respeitam as capacidades. O último fluxo é máximo pois não há pseudocaminho aumentador para ele.

Exercícios 3

Para que serve o algoritmo de Ford-Fulkerson? Que problema resolve? Quais são os dados desse problema?
★ Como começa uma iteração genérica do algoritmo de Ford-Fulkerson? (Cuidado! Não quero uma descrição das ações que ocorrem no início de uma iteração! Quero saber, isto sim, quais as informações disponíveis no início de uma iteração genérica, antes que a execução da iteração comece.)
Encontre um fluxo máximo no grafo capacitado definido pela tabela abaixo. Suponha que o vértice inicial é 0 e o final é 3. Comece com um fluxo ao longo do caminho 0-1-2-3.
```
0-1 0-2 1-2 1-3 2-3 
 12  15  20  19  11 
```
Encontre um fluxo máximo no grafo capacitado da figura. Suponha que o vértice inicial é 9 e o final é 6.
★ Fluxo inteiro. Suponha que todas as capacidades de um grafo capacitado são números inteiros. Mostre que o fluxo em cada arco permanece inteiro ao longo da execução do algoritmo de Ford-Fulkerson.
★ Caminhos aumentadores. Um caminho aumentador é um pseudocaminho aumentador sem arcos reversos. Mostre que o algoritmo de Ford-Fulkerson pode não produzir um fluxo máximo se usar apenas caminhos aumentadores.

Desempenho do algoritmo

O consumo de tempo do algoritmo de Ford-Fulkersonal é proporcional ao número de iterações. Tudo se reduz, portanto, à seguinte questão: Quantos pseudocaminhos aumentadores são necessários para produzir um fluxo máximo a partir do fluxo nulo?

Prova: Como as capacidades dos arcos são números inteiros, o fluxo em cada arco é um número inteiro. Portanto, ao longo da execução do algoritmo, a capacidade residual de cada arco em qualquer pseudocaminho aumentador é um número inteiro positivo. Logo, cada pseudocaminho aumentador tem capacidade residual pelo menos 1 e assim aumenta em pelo menos 1 a intensidade do fluxo.

Resta apenas mostrar que não existe fluxo de intensidade maior que V M. Como não temos arcos paralelos, o número de arcos que saem do vértice inicial é menor que V. Portanto, qualquer fluxo tem intensidade menor que V M. (Esse raciocínio é um caso particular da delimitação superior por capacidade de cortes que veremos adiante.)

Essa estimativa do número de pseudocaminhos aumentadores não é excessivamente pessimista: existem grafos capacitados (veja o exemplo abaixo) em que o número de pseudocaminhos aumentadores chega muito perto de V M.

Como o número de pseudocaminhos aumentadores depende das capacidades dos arcos, o algoritmo não pode ser considerado satisfatório: a mera multiplicação de todas as capacidades por 100, por exemplo, pode multiplicar o consumo de tempo por 100. (Em linguagem técnica, diz-se que o algoritmo é apenas fracamente polinomial.) Para obter um desempenho que não dependa das capacidades será preciso escolher os pseudocaminhos aumentadores de maneira mais cuidadosa. É o que faremos nos próximos capítulos.

Exemplo G. Considere o seguinte grafo capacitado com vértice inicial 0 e vértice final 3:

Começando com fluxo nulo, tome a seguinte sequência periódica de pseudocaminhos aumentadores:

O fluxo tem intensidade 2M e o número de iterações é 2M. Como V = 4, o número de iterações é (V-2)M. Esse exercício mostra que o número de pseudocaminhos aumentadores no algoritmo de Ford-Fulkerson pode chegar muito perto de VM.

(É bem verdade que poderíamos atingir o fluxo máximo em apenas duas iterações se os pseudocaminhos aumentadores fossem escolhidos de maneira diferente. Mas a versão do algoritmo dada acima não ensina como escolher bons pseudocaminhos aumentadores.)

Exercícios 4

Um caminho aumentador é um pseudocaminho aumentador sem arcos reversos. É verdade que existe uma sequência de caminhos aumentadores que leva do fluxo nulo ao fluxo máximo?
[Sedgewick 22.21] Considere o grafo capacitado abaixo, com vértice inicial 0 e vértice final 5. Mostre, no estilo do exemplo E, uma sequência de pseudocaminhos aumentadores que leva a um fluxo máximo. Mostre outra sequência, diferente da primeira. Mostre mais uma, diferente das anteriores.
```
0-1 0-2 0-3 1-2 1-3 1-4 2-4 2-5 3-4 3-5 4-5 
  2   3   2   1   1   1   1   2   2   3   2  
```
[Sedgewick 22.41] Considere o grafo capacitado abaixo, com vértice inicial 0 e vértice final 5. Dê uma sequência de pseudocaminhos aumentadores que produza um fluxo com ciclo (ou seja, um fluxo cuja decomposição em caminhos e ciclos tenha um ciclo). Cada um dos pseudocaminhos aumentadores deve ser simples (ou seja, não pode ter vértices repetidos).
```
0-1 0-2 0-3 1-3 1-4 2-1 2-5 3-4 3-5 4-2 4-5 
  2   3   2   1   1   1   2   2   3   1   2  
```
Emparelhamento em grafo não-dirigido bipartido. Como o algoritmo de Ford-Fulkerson pode ser usado para encontrar um emparelhamento máximo num grafo não-dirigido bipartido? (Será preciso modificar o grafo antes de aplicar o algoritmo.) Aplique sua técnica ao grafo não-dirigido bipartido a seguir. Um dos lados do grafo consiste nos vértices 0 1 2 3 4 e outro consiste nos vértices 5 6 7 8 9 .
```
0-5 0-6 1-5 1-6 2-5 2-6 3-5 3-7 3-8 3-9 4-6 4-7 4-8 4-9
```
Capacidades nos vértices. Seja G um grafo com vértice inicial e vértice final e com capacidades nos vértices (mas sem capacidades nos arcos). Como calcular um fluxo máximo dentre os que respeitam as capacidades?

Exercícios 5

★ Implementação com matriz. É difícil implementar o algoritmo de Ford-Fulkerson porque é difícil calcular pseudo caminhos, especialmente em grafos representados por listas de adjacência. A dificuldade é menor se o grafo é representados por matriz de adjacência. Suponha então que nosso grafo é representado por uma matriz de capacidades cap[][] que substitui a matriz de adjacência: para cada par v w de vértices, cap[v][w] > 0 se e somente se v-w é um arco. Um fluxo no grafo pode ser representado por uma matriz f[][] com linhas e colunas indexadas pelos vértices. Para procurar um pseudocaminho aumentador, basta fazer uma busca em largura ligeiramente modificada: para examinar os arcos que saem de v, percorra a linha v de cap[][], e para examinar os arcos que entram em v (arcos reversos do pseudocaminho), percorra a coluna v de cap[][]. Use essas ideias para implementar o algoritmo de Ford-Fulkerson.