Cliques e conjuntos estáveis em grafos

Uma clique em um grafo não-dirigido é um conjunto de vértices dois a dois adjacentes. Em outras palavras, um conjunto C de vértices é uma clique se tiver a seguinte propriedade: para todo par (v, w) de vértices distintos em C, existe uma aresta com pontas v e w.

Exemplo: para qualquer vértice v, o conjunto { v } é uma clique. Outro exemplo: se o grafo tem alguma aresta com pontas v e w então o conjunto { v, w } é uma clique.

Uma clique C é maximal se não existe clique C' que seja superconjunto próprio de C. Uma clique C é máxima se não existe clique C' que seja maior que C. Encontrar uma clique maximal é fácil (veja próxima seção); encontrar uma clique máxima é mais difícil.

Esse problema aparece naturalmente em muitas aplicações práticas. Às vezes é conveniente reformulá-lo assim:

Problema da Clique Grande: Dado um grafo e um número natural k, encontrar uma clique com k ou mais vértices.

É claro que esta segunda versão do problema pode não ter solução (por exemplo, se o grafo todo tem menos que k vértices).

Exercícios 1

Escreva uma função C que verifique se um dado conjunto de vértices é ou não uma clique. (A presença de laços é irrelevante.) Suponha que o conjunto é dado por meio de um utility field: vmarca ≡ 1 se e só se v está no conjunto.
Encontre uma clique máxima no grafo product (circuit (5), circuit (3), 2, 0). As funções product e circuit estão definidas nos blocos 94 e 7 do módulo GB_BASIC. Faça uma figura do grafo. (Sugestão: use uma adaptação da tarefa de programação A para ver o grafo.)

Cliques maximais

O problema de calcular cliques maximais é muito fácil e não deveria merecer muita atenção. Ainda assim, vamos discutir um pouco o assunto.

O seguinte processamento sequencial (você tem um nome melhor?) dos vértices é trivial mas útil. Suponha dada uma ordenação dos vértices do grafo, ou seja, uma sequência v₀, v₁, … , v_n−1 em que cada vértice aparece uma e uma só vez. (Essa permutacão não tem relação alguma com a ordem em que os vértices aparecem no vetor gvertices na estrutura de dados do SGB.) Para encontrar uma clique maximal C a partir dessa ordenação, basta fazer

C = { v₀ }

para k = 1 até n−1 faça

se v_k é vizinho de todos os vértices em C

então C = C ∪ { v_k }

Observe que, no início de cada iteração, C é uma clique e faz parte do conjunto { v₀, v₁, … , v_k−1 }.

Exercícios 2

Mostre que o processamento sequencial dos vértices produz uma clique maximal, qualquer que seja a ordenação v₀, v₁, … , v_n−1 adotada.
Escreva uma função C que implemente o processamento sequencial usando a ordenação dos vértices dada pelo vetor vertices: v₀ ≡ gvertices, v₁ ≡ gvertices + 1, etc. A função pode devolver a clique maximal por meio de um utility field: vclq vale 1 se v está na clique e 0 em caso contrário. A função pode também devolver o tamanho da clique maximal encontrada.
Escreva uma função C que implemente o processamento sequencial a partir de uma ordenação arbitrária dos vértices. A função recebe um vértice v e a ordenação v, vprox, vproxprox, etc. dos vértices. A função pode devolver a clique maximal por meio de um utility field: vclq vale 1 se v está na clique e 0 em caso contrário.
Escreva uma função C que receba um grafo g e um vértice v e encontre uma clique maximal que contenha v.
É verdade que todas as cliques maximais de um grafo têm o mesmo tamanho?
Discuta o seguinte algoritmo que encontra uma clique máxima: faça uma lista de todas cliques maximais e escolha a maior. Mais detalhes: faça uma lista de todos os subconjuntos do conjunto de vértices; descarte os conjuntos que não são cliques; escolha o maior dos que sobrarem. (Para economizar espaço, podemos representar cada conjunto de vértices por um vetor de bits.)

Cliques máximas

Infelizmente, não sei encontrar, de maneira eficiente, uma clique máxima em um grafo não-dirigido arbitrário. Mas sei resolver o problema em certos grafos especiais, como os grafos de intervalos que estudaremos num próximo capítulo.

Exercícios 3

Dê exemplos para mostrar que a diferença entre os tamanhos de uma clique máxima e uma clique maximal pode ser arbitrariamente grande. Em outros palavras, para cada k, dê um grafo (de preferência conexo) que tenha uma clique com k ou mais vértices e uma clique maximal com apenas 2 vértices.
Coloque os vértices do seu grafo em ordem decrescente de grau: g(v₀) ≥ g(v₁) ≥ … Aplique o processamento sequencial de vértices discutido na seção anterior. A clique resultante é máxima? E se os vértices estiverem em ordem crescente de grau?
Mostre que todo grafo admite uma ordenação v₀, v₁, … , v_n−1 dos vértices para a qual o processamento sequencial discutido na seção anterior produz uma clique máxima.
Implemente o seguinte algoritmo para encontrar uma clique máxima: para cada vértice v, faça uma lista de todos os subconjuntos do conjunto de vizinhos de v; descarte os subconjuntos que não são cliques; escolha o maior dos que sobrarem. O algoritmo é eficiente? Em que condições ele é razoável?
Encontre a maior clique que puder no grafo games (120, 0, 0, 1, 2, 0, 0, 0) definido no módulo GB_GAMES do SGB. Cada vértice desse grafo é um de 120 times de football americano; dois vértices são adjacentes se os correspondentes times se enfrentaram na temporada de 1990.
Encontre a maior clique que puder no grafo book ("jean", 0, 0, 1, 356, 0, 0, 0) definido no módulo GB_BOOKS do SGB. Cada vértice desse grafo é um personagem do livro Os miseráveis de Victor Hugo. Dois vértices são adjacentes se os correspondentes personagens se encontram durante a trama do livro.

Conjuntos estáveis

Um conjunto de vértices em um grafo não-dirigido é estável (= stable) ou independente se seus elementos são dois a dois não-adjacentes. Em outras palavras, um conjunto E de vértices é estável se não existe aresta com ambas as pontas em E.

Exemplo: Para qualquer vértice v, o conjunto { v } é estável se não existe laço da forma vv. Outro exemplo: se v e w são vértices distintos e não existe aresta com pontas v e w então o conjunto { v, w } é estável.

Conjuntos estáveis estão intimamente relacionados com cliques: um conjunto E de vértices é estável em um grafo (estamos supondo implicitamente que nosso grafo não tem laços) se e só se E é uma clique no grafo complementar.

Um grafo G é complementar a outro H se ambos têm o mesmo conjunto de vértices e existe uma aresta com pontas v e w em G se e só se não existe uma tal aresta em H. A propósito, o bloco 73 do módulo GB_BASIC do SGB define uma função complement que recebe um grafo e devolve o seu complemento. (Você deve dizer complement (g, 0, 1, 0) para obter o complemento de g.)

Conjuntos estáveis maximais e máximos são definidos da maneira óbvia. Dado um algoritmo para encontrar uma clique maximal é fácil transformá-lo em um algoritmo que encontra um conjunto estável máximal; e vice-versa. Afimação análoga vale para cliques máximas e conjuntos estáveis máximos. Portanto, os problemas abaixo são equivalentes ao problema da clique máxima:

Problema: Dado um grafo e um número natural k, encontrar um conjunto estável com k ou mais vértices.

Exercícios 4

Escreva uma função C que verifique se um dado conjunto de vértices é ou não estável. Suponha que o conjunto é dado por meio de um utility field: vmarca ≡ 1 se e só se v está no conjunto.
Mostre um exemplo simples em que um conjunto estável maximal não é máximo.
Suponha que um certo conjunto de eventos quer usar um centro de convenções. Cada evento tem uma data de início e uma data de fim. O centro não pode atender dois eventos simultâneos. Encontrar um conjunto máximo de eventos que o centro de convenções pode atender.
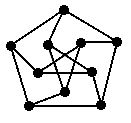Faça uma lista de todos os conjuntos estáveis maximais no grafo da figura. Esse é o famoso grafo de Petersen. Para o SGB, esse grafo é disjoint_subsets (5, 2). A função disjoint_subsets está definida no bloco 36 do módulo GB_BASIC.
Faça uma lista de todos os conjuntos estáveis maximais no grafo board (5, 5, 0, 0, 1, 0, 0). A função board está definida no bloco 6 e seguintes do módulo GB_BASIC do SGB. Faça uma figura do grafo. (Sugestão: use uma adaptação da tarefa de programação A para ver o grafo.)
Encontre um conjunto estável máximo no grafo product (circuit (5), circuit (3), 2,0). As funções product e circuit estão definidas nos blocos 94 e 7 do módulo GB_BASIC. Faça uma figura do grafo. (Sugestão: use uma adaptação da tarefa de programação A para ver o grafo.)

Coberturas

Uma cobertura (= vertex cover) de um grafo não-dirigido é um conjunto K de vértices dotado da seguinte propriedade: cada aresta do grafo tem pelo menos uma ponta em K.

A relação entre coberturas e conjuntos estáveis é muito simples: num grafo com conjunto de vértices V, se K é uma cobertura então V−K é um conjunto estável. Reciprocamente, se S é um conjunto estável então V−S é uma cobertura. Segue daí imediatamente um conjunto estável S é máximo se e só se a cobertura V−S é mínima. Conclusão: Encontrar um conjunto estável máximo é o mesmo que encontrar uma cobertura mínima.

Exercícios 5

É verdade que um conjunto K de vértices é uma cobertura se e só se cada vértice v em K é ponta inicial de um arco do grafo?
Suponha que G é um grafo não-dirigido com conjunto de vértices V. Seja K uma cobertura mínima e C uma clique máximo. É verdade que C ≡ V − K?
O seguinte algoritmo faz uma lista de todas coberturas minimais para mais tarde escolher uma mínima. Digamos que os vértices do grafo são v₀, v₁, … , v_n−1. Para cada i, seja S_i a estrela de v_i, isto é, o conjunto formado por v_i e todos os seus vizinhos. No começo de uma iteração genérica, o algoritmo já tem uma lista de todas coberturas minimais do grafo induzido por S₀ ∪ … ∪ S_i−1. Durante essa iteração, o algoritmo troca cada elemento K da lista por dois conjuntos:
K ∪ { v_i } e K ∪ (S_i − { v_i }).
No fim da última iteração, o algoritmo retira da lista todos os conjuntos não minimais. Prove que a lista final tem todas as coberturas minimais do grafo. Em que condições essa algoritmo pode ser útil na prática?