Description
The problem of estimating the thickness and the optical constants
of thin films using transmission data only is very challenging from
the mathematical point of view, and has a technological and an
economic importance. In many cases it represents a very
ill-conditioned inverse problem with many local-nonglobal
solutions. In a recent publication, we proposed nonlinear
programming models for solving this problem. Well-known software
for linearly constrained optimization was used with success for
this purpose.
In this page, we describe very briefly, how to install and use the
software PUMA which implements an
unconstrained formulation of the nonlinear programming model, which
solves the estimation problem using a method based on repeated
calls to a recently introduced unconstrained minimization
algorithm. Numerical experiments on computer-generated films show
that the new procedure is reliable.
This page is organized as follows:
Conditions of use
PUMA is free for non-commercial use
only. It may be distributed within a "Research Group" but not
distributed to third parties without the developer's
authorization. The code must not be included in any commercial package
without previous agreement. Every published work that uses PUMA must cite:
E. G. Birgin, I. Chambouleyron, and J. M. Martínez,
Estimation of
optical constants of thin films using unconstrained optimization,
Journal of Computational Physics 151, pp. 862-880, 1999.
(See also other PUMA's related works.)
Download
This section guides you on how to download PUMA. People interested in downloading PUMA are kindly requested to fill-in the boxes
below. The information is confidential and it will just be used for
academic purposes. PUMA is available at no
cost, provided that simple
conditions-of-use are obeyed. A potential user must read and
accept these before downloading the software.
Problems downloading PUMA? Please,
write to egbirgin@ime.usp.br.
Installation
Sequential version (recommended for one-film systems)
To proceed installation in a SUN, Solaris or
Linux platform, just follow these steps:
- To compile (install) the software, you have to have installed the
GCC compiler (compiler of
C from GNU, freely distributed at GNU
Project Page) or any other compatible compiler.
- Once you have the appropriate compiler, you can compile it by
writing in a terminal the following command line:
gcc -O4 -lm puma.c -o puma
This will produce a binary file puma, that is the file
actually used.
To proceed installation in a Windows platform, just follow these steps:
- To compile (install) the software, you have to have installed the
Dev-C++ compiler (C/C++
compiler for Windows,
freely distributed at Bloodshed
Software) or any other compatible compiler.
- Once you have the appropriate compiler, you can compile it
by clicking in the menu item COMPILE and then in the menu item
RUN.
This will produce a binary file puma.exe, that is the file
actually used.
If you managed to do this, you successfully installed
PUMA.
Parallel version (recommended for systems with two or more films)
To proceed installation in a SUN, Solaris or
Linux platform, just follow these steps:
- To compile (install) the software, you have to have installed the
MPICC compiler (wrapper to the
GNU C compiler for MPI applications, freely available with major MPI
implementations like, for example,
LAM/MPI) or any other compatible
compiler.
- Once you have the appropriate compiler, you can compile it by
writing in a terminal the following command line:
mpicc -O4 -lm puma-par.c -o puma-par
This will produce a binary file puma-par, that is the file
actually used.
If you managed to do this, you successfully installed
PUMA.
How to Use
To run PUMA for estimating the thickness and
the optical constants of a one-film system just type in a terminal the
following sequence
puma FNAME NLAYERS SLAYER SUBSTRATE DATATYPE NOBS LAMBDAmin
LAMBDAmax maxIT QUAD INIT THICKNESSmin THICKNESSmax THICKNESSstep INFLEmin
INFLEmax INFLEstep N0ini N0fin N0step NFini NFfin NFstep K0ini K0fin K0step
where the capitalized words are parameters, described by
FNAME is a string (without blanks)
representing the name of the film being studied. The input data
file name must be in the format FNAME-dat.txt
(the output file name will be automatically created adding
"-inf.txt", so that is looks like
FNAME-inf.txt). The input file should be
structured as follows (see the example below):
a) the first line must contain the number of observations. If for
example, you have 100 observations, the whole input file will have
101 lines.
b) from the second to the last line, it must contain, in each
line, the wavelength and the transmittance (reflectance or
both). This means that, from the second to the last line, there
have to be either 2 or 3 numbers.
c) the observed data. i.e., transmittance (reflectance or both)
has to be given in fractions, ranging from 0 up to 1. In
this way, you must divide the measured data by 100 if they are
given in percentages, ranging from 0 up to 100.NLAYERS is the number of layers of
the whole system, that is, the films, the substrate
and the initial and final air layers. The present version
works with only four layers, that is, one film. For systems with more
than one film, see the parallel version
of PUMA.SLAYER is the number of the layer
that corresponds to the substrate. For systems composed, from top
to bottom, first air layer (layer 0), film (layer 1), substrate
(layer 2) and last air layer (layer 3) set SLAYER
equal to 2.SUBSTRATE is a number describing the
substrate. Use 10 for Corning 7059 glass substrate,
20 for crystalline silicon substrate, 30 for
crystalline quartz substrate, 40 for glass slides substrate
and 50 for borosilicate substrate.DATATYPE is a character describing the data
type. Use T for transmittance data, R for
reflectance data and B for both.NOBS is the number of points used in
the optimization process. They are equally spaced points,
interpolated inside the interval given by the parameters
LAMBDAmin and LAMBDAmax (see
below). This parameter is
independent of the number of points furnished by the input
file (FNAME-dat.txt).We strongly
recommend you to use 100 points if you have not experience or are
uncertain about this parameter.LAMBDAmin is the left bound of the
interval in which the optical constants will be estimated
(LAMBDAmin must be greater than or equal to the
smallest wavelength for which the measured data is provided in
FNAME-dat.txt file).LAMBDAmax is the right bound of the
interval in which the optical constants will be estimated
(LAMBDAmax must be smaller than or equal to the
greatest wavelength for which the measured data is provided in
FNAME-dat.txt file). Note that
LAMBDAmax >= LAMBDAmin is
mandatory.MAXIT is the maximum number of
iterations for the optimization solver. For each combination of
fixed THICKNESS and
INFLEPOINT (as determined in items 10 and 13) a
nonlinear optimization problem is solved to estimate the optical
constants 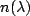 and
and 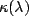 . We recommend you to use
3000 for the first trial, 5000 for the second trial, and 50000 for
the last one.
. We recommend you to use
3000 for the first trial, 5000 for the second trial, and 50000 for
the last one.QUAD is the quadratic error of the
best optical constants estimation you have. Only quadratic error
values smaller than QUAD are saved. In the
first trial, we recommend to use a big number, such as
1e+100. When using the previous best estimation as the initial
guess for a new trial, if may happen that, in this new trial, no
better estimation is found. In this case, the returned
retrieved thickness is zero.INIT is an integer for choosing
between either perform the initial estimative (in this case use
0), or use previous estimation as initial guess (in this
case use 9). In the last case, i.e., when using the
previously estimated optical constants to guide a new trial
(INIT=9), the remaining parameters
N0ini, N0fin, N0step,
NFini, NFfin, NFstep,
K0ini, K0fin and K0step are
ignored.THICKNESSmin is the trial
thicknesses lower bound. This parameter, together with the next
one must define an interval
[THICKNESSmin,THICKNESSmax] inside of
which you know that the real thickness you are trying to retrieve
is. So, some kind of a priori knowledge of the thickness
of the material is necessary to set this parameters.THICKNESSmax is the trial
thicknesses upper bound. Note that THICKNESSmax
>= THICKNESSmin is mandatory. Using
THICKNESSmax = THCIKNESSmin means that
you know the real thickness and that just the optical constants
will be retrieved. In this case (in which
THICKNESSmin=THICKNESSmax), the
THICKNESSstep is ignored.THICKNESSstep is the trial
thicknesses step. When trying to retrieve the real thickness
inside the interval
[THCIKNESSmin,THICKNESSmax], all the
values given by
THICKNESS =
THICKNESSmin + w *
THICKNESSstep,w = 0, 1, 2, ...
INFLEmin is the attenuation
coefficient inflection point lower bound. In the PUMA
approach, the attenuation coefficient
function 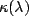 is approximated
by a function, which is concave in the interval
[
is approximated
by a function, which is concave in the interval
[LAMBDAmin,INFLEPOINT] and
convex in the interval [INFLEPOINT,LAMBDAmax].
This
parameter, together with the next one must define an interval
[INFLEmin,INFLEmax] inside of which the
real inflection point is. If you have not any
a priori knowledge of where it is, use
INFLEmin=LAMBDAmin.INFLEmax is the attenuation
coefficient inflection point upper bound. Note that
INFLEmax >= INFLEmin is
mandatory. If you have not any
a priori knowledge of where it is, use
INFLEmax=LAMBDAmax. Using
INFLEmax = INFLEmin means that you know
where the inflection point is. For example, if you know that in
the interval [LAMBDAmin,LAMBDAmax] 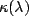 is a convex function, then set
is a convex function, then set
INFLEmin=LAMBDAmin and
INFLEmax=LAMBDAmin. In this case (in
which INFLEmin=INFLEmax), the
INFLEstep is ignored.INFLEstep is the attenuation
coefficient inflection point step. When trying to retrieve the
real inflection point inside the interval
[INFLEmin,INFLEmax], all the values
given by
INFLEPOINT =
INFLEmin + w * INFLEstep,w
= 0, 1, 2, ...
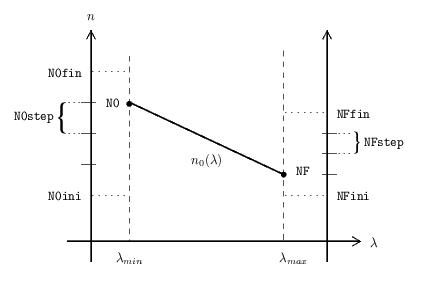
N0ini, N0fin,
N0step, NFini, NFfin,
NFstep refer to the initial estimative of the
refractive index 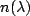 (see
figure below). The initial estimates of the refractive index are
the strictly decreasing linear functions which values vary between
(see
figure below). The initial estimates of the refractive index are
the strictly decreasing linear functions which values vary between
N0ini and N0fin with step
N0step at LAMBDAmin and between
NFini and NFfin with step NFstep
at LAMBDAmax. So, the strictly decreasing linear
functions used as initial estimates of 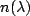 are the linear functions which pass through
the pairs:
are the linear functions which pass through
the pairs:
(LAMBDAmin,N0), (LAMBDAmax,NF)
with
N0 =
N0ini + u * N0step,
u = 0, 1, 2, ...
NF =
NFini +
v * NFstep, v = 0, 1, 2, ...
N0 in
[N0ini,N0fin], NF in
[NFini,NFfin], and N0 > NF.
An a priori knowledge of the refractive index of the
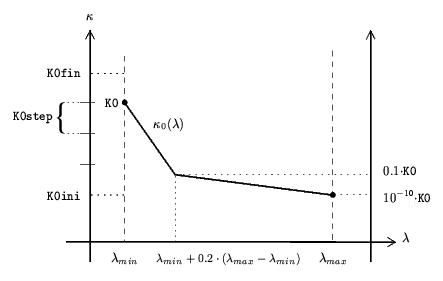
material is needed to set these parameters.K0ini, K0fin,
K0step refer to the initial estimates of the
attenuation coefficient 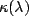 (see figure below). In this case, we used a piecewise linear
function, the values of which are
(see figure below). In this case, we used a piecewise linear
function, the values of which are K0 at
LAMBDAmin, 0.1*K0 at
LAMBDAmin+0.2*(LAMBDAmax-LAMBDAmin)
and 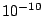 *
*K0 at LAMBDAmax,
where K0 takes on the values
| K0 = K0ini
+ z * K0step,z = 0, 1, 2,
...
|
inside the interval
[K0ini,K0fin].
Remark: Parameters described in 18 and 19 are meaningful only if you
want to perform an initial estimative (when you set INIT=0);
otherwise, they must be omitted. For systems with two or more films,
if INIT=0 then parameters described from 12 to 19 must be
repeated for each film. For systems with two or more films, if
INIT=9 then parameters described from 12 to 17 must be
repeated for each film.
One-film system example
As explained above, you can call PUMA
either performing an initial estimative or using a previous
estimate as initial guess, calling PUMA one,
two, three or more times, as long
as you find it necessary. This fact, combined with some clever
choice of the input parameters in the sequence of calls, gives
PUMA a good degree of
flexibility.
Because, most of the time, it is enough to make three calls,
we recommend, as a default procedure, to perform three calls,
as follows.
- In the first trial, chose an interval for the trial thicknesses
around some value. Set the thickness step. Choose the attenuation
coefficient inflection point interval to be the same of the
spectrum interval.
- Narrow the trial thicknesses interval around the previous
retrieved thickness. Decrease the thickness step. Do the same for
the attenuation coefficient inflection point. Increase the maximum
number of iterations.
- Fix the thickness as the previous retrieved thickness. Do the same
for the inflection point. Once again, increase the maximum number
of iterations.
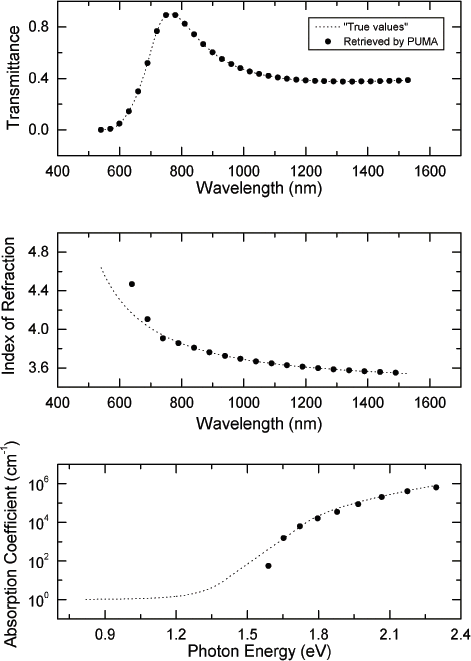
As an example, suppose we have the gedanken film A of
[1] (to reproduce this example in your computer,
copy the input data file sigl0097t-dat.txt in the same
directory where PUMA was installed). The
trial sequence is as follows.
First Call
For the first trial, we have
puma sigl0097t 4 2 10 T 100 0540 1530 3000 1e+100 0
0010 0200 10 0540 1530 100 3 5 1 3 5 1 0.10 0.10 0.05
In this statement, we used
FNAME: sigl0097t. This film was generated
using gedanken constants and simulates an a a-Si:H thin
film deposited on a glass substrate with thickness of 97nm (see
the file sigl0097t-dat.txt).NLAYERS: 4 (first air layer + 1 film +
substrate + last air layer)SLAYER: 2 (the first air layer is called layer 0,
the film is layer 1, the substrate is layer 2 and the last air
layer is layer 3)SUBSTRATE: 10 (Corning 7059 glass).DATATYPE: T (transmittance).NOBS: 100 (as recommended).LAMBDAmin: 540 and LAMBDAmax:
1530. Note that the in the input file, the smallest wavelength is
1 and the greatest one is 5000.MAXIT: 3000QUAD: 1e+100INIT: 0. That means we are running the initial
estimative.THICKNESSmin: 10, THICKNESSmax: 200 and
THICKNESSstep: 10INFLEmin: 540 , INFLEmax: 1530 and
INFLEstep: 100N0ini: 3, N0fin: 5, N0step:
1, NFini: 3, NFfin: 5,
NFstep: 1K0ini: 0.10, K0fin: 0.10,
K0step: 0.05
You can see the first output file
sigl0097t-inf.txt or the
terminal output during this run. The
retrieved thickness was 100nm, the retrieved attenuation
coefficient inflection point was 540nm and the retrievals of the
refractive index and the attenuation coefficient at
the end of this run, were
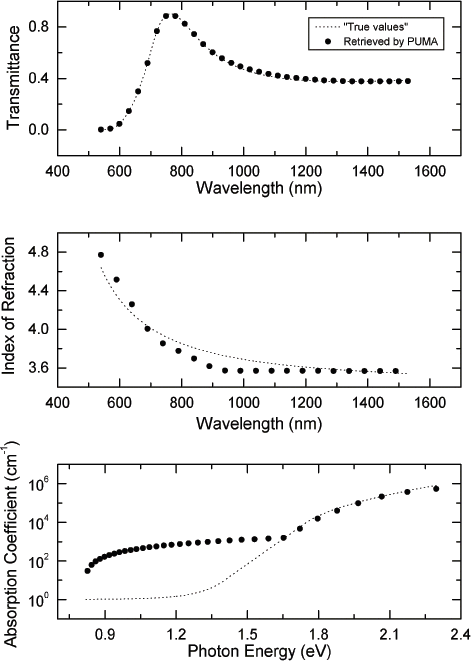
Second Call
Once the first trial is finished, you can go to the second
trial. If you look at the output file sigl0097t-inf.txt of the first call,
you can see that the retrieved thickness was 100nm, the retrieved
inflection point was 540nm and the quadratic error was
6.342857e-03. This last value may vary slightly from machine to
machine, so do not expect to reproduce it exactly. With this
at hand, we can go to the second trial:
puma sigl0097t 4 2 10 T 100 0540 1530 5000
6.342857e-03 9 0050 0150 01 0540 0540 100
where the bold font means which parameters were changed from the
first call. Their meanings are
- We increased the number of iterations from 3000 to 5000.
- We made
QUAD="previous quadratic error"=
6.342857e-03. This means that only thicknesses and constant
estimations with a quadratic error smaller than this one will be
saved.
- As we are using the previously estimated optical constants to
guide this new trial, we must set
INIT=9.
- For the new thickness interval, we choose the one centered at 100
(obtained previously), with +/- 50 of amplitude. Also, we
decreased the step to 1.
- As the retrieved value for the inflection point is considered
good, we fixed it at 540 by making
INFLEmin =
INFLEmax = 540. In this case the
INFLEstep is not considered at all and it can take
any value).
- The remaining parameters
N0ini, N0fin,
N0step,NFini, NFfin,
NFstep, K0ini, K0fin, and
K0step (which were only needed at the first call) must
be omitted.
You can see the second output file sigl0097t-inf.txt or the terminal output during this run. The
retrieved thickness was 97nm and the retrievals of the
refractive index and the attenuation coefficient at
the end of this run, were
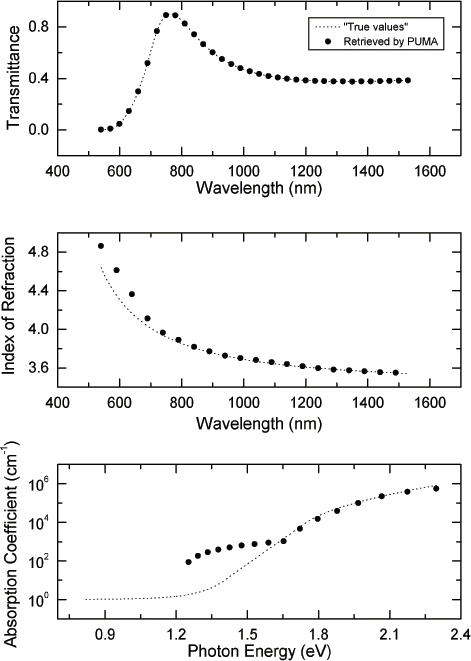
Third Call
Finally, you can go to the third and last trial. If you look at the
output file sigl0097t-inf.txt of
the second call, you can see that the retrieved thickness is 97nm
and the best quadratic error decreased to 1.773782e-04 (remember
that the inflection point was fixed at 540nm). With this at hand,
you can go the third and last trial:
puma sigl0097t 4 2 10 T 100 0540 1530 50000
1.773782e-04 9 0097 0097 01 0540 0540 100
where the bold font means, as before, which parameters were
changed from the previous call. Their meanings are
- We increased the number of iterations from 5000 to 50000.
- We made
QUAD="previous quadratic error"=
1.773782e-04. This means that only thicknesses and constant
estimations with a quadratic error smaller than this one will be
saved.
- We considered the thickness as retrieved, with value 97nm. So we
fix it by making
THICKNESSmin =
THICKNESSmax = 97. In this case the
THICKNESSstep is not considered at all and it can
take any value).
You can see the last output file
sigl0097t-inf.txt or the
terminal output during this run. The
retrievals of refractive index and the attenuation
coefficient at the end of this run, were
Two-films system example
As a second example, suppose we have the gedanken film AgB of
[7] (to reproduce this example
in your computer, copy the input data file
AgB01000600t-dat.txt in the same
directory where PUMA was installed). The trial
sequence is as follows. Before running the parallel version of PUMA
do not forget to start up your MPI Grid.
First Call
First of all, copy the executable file puma-par and the data file
AgB01000600t-dat.txt to all
the nodes of your MPI Grid.
For the first trial, submit to your MPI Grid, the following:
puma-par AgB01000600t 5 2 10 T 100 631 1621 5000 1e+100 0 50 150 10 631 631 1 3.5 4.5 0.5 3 4 0.5 0.5 0.5 1 550 650 10 631 631 1 3.5 4.5 0.5 3 4 0.5 0.5 0.5 1
In this statement, we used
FNAME: AgB01000600t. This film was generated using gedanken
constants and simulates an a-Si:H thin film with tickness of 100nm deposited on
one side of a glass substrate and an a-Si:H thin film with thickness of 600nm
deposited on the other side of the glass substrate (see the file
AgB01000600t-dat.txt).NLAYERS: 5 (first air layer + film A +
substrate + film B + last air layer)SLAYER: 2 (the first air layer is called layer 0,
the first film is layer 1, the substrate is layer 2, the second
film is layer 3 and the last air layer is layer 4).SUBSTRATE: 10 (Corning 7059 glass).DATATYPE: T (transmittance).NOBS: 100 (as recommended).LAMBDAmin: 631 and LAMBDAmax:
1621.MAXIT: 5000QUAD: 1e+100INIT: 0. That means we are running the initial
estimative.Parameters related to the first film (Film A):
THICKNESSmin: 50, THICKNESSmax: 150 and
THICKNESSstep: 10INFLEmin: 631 , INFLEmax: 631 and
INFLEstep: 1N0ini: 3.5, N0fin: 4.5, N0step:
0.5, NFini: 3, NFfin: 4,
NFstep: 0.5K0ini: 0.50, K0fin: 0.50, K0step: 1Parameters related to the second film (Film B):
THICKNESSmin: 550, THICKNESSmax: 650 and
THICKNESSstep: 10INFLEmin: 631 , INFLEmax: 631 and
INFLEstep: 1N0ini: 3.5, N0fin: 4.5, N0step:
0.5, NFini: 3, NFfin: 4, NFstep: 0.5K0ini: 0.50, K0fin: 0.50,
K0step: 1
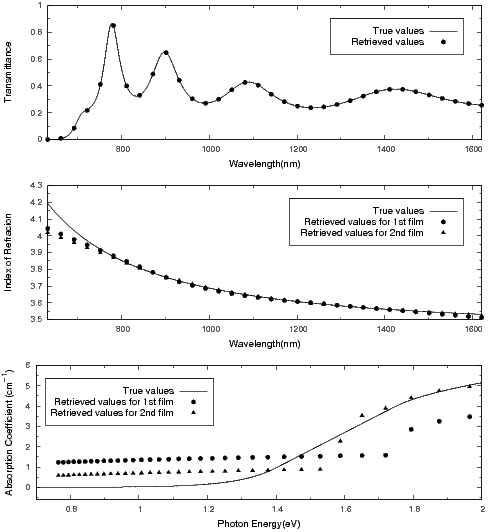
You can see the first output file
AgB01000600t-inf.txt or the
terminal output during this run
(note that because of the nondeterministic order of execution of the
subproblems, your output lines may be in a different order). The
retrieved thicknesses were 100nm and 600nm for the first and the second film,
respectively; while the retrievals of the refractive indexes and the
attenuation coefficients at the end of this run, were
Second Call
First of all, copy file AgB01000600t-sol.txt (generated by the
previous call to PUMA) to all the nodes of
your MPI Grid.
Once the first trial is finished, we can go to the second
trial. If you look at the output file
AgB01000600t-inf.txt
of the first call,
you can see that the retrieved thicknesses were 100nm and 600nm
for the first and the second film, respectively;
while the quadratic error was 3.744793e-04. This last value may vary
slightly from machine to machine, so do not expect to reproduce
it exactly. With this at hand, we can go to the second trial.
For the second trial, submit to your MPI Grid, the following:
puma-par AgB01000600t 5 2 10 T 100 631 1621 100000 3.744793e-04 9 50 150 1 631 631 1 550 650 1 631 631 1
where the bold font means which parameters were changed from the
first call. Their meanings are
- We increased the number of iterations from 5000 to 100000.
- We made
QUAD="previous quadratic error"=
3.744793e-04. This means that only thicknesses and constant
estimations with a quadratic error smaller than this one will be
saved.
- As we are using the previously estimated optical constants to
guide this new trial, we must set
INIT=9.
- For the new thicknesses intervals, we choose the ones centered
at the previously obtained values, with +/- 50 of amplitude
(no changes from last run). Also, we
decreased the step to 1.
- The remaining parameters (for both films)
N0ini,
N0fin, N0step,NFini,
NFfin, NFstep, K0ini,
K0fin, and K0step (which were
needed at the first call) must be omitted.
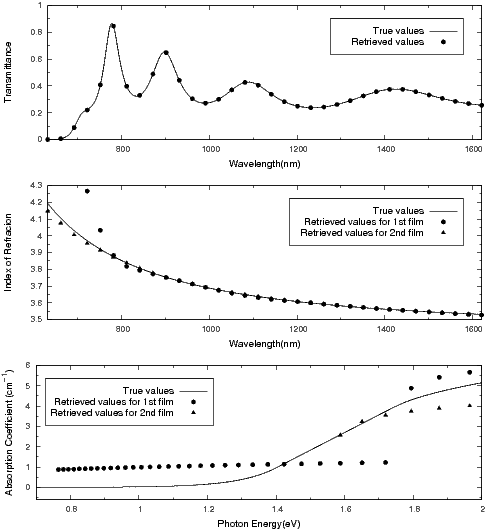
You can see the second output file
AgB01000600t-inf.txt or the
terminal output during this run
(note that because of the nondeterministic order of execution of the
subproblems, your output lines may be in a different order). The
retrieved thicknesses were 100nm and 600nm for the first and the second
film, respectively; the retrievals of the
refractive indexes and the attenuation coefficients at
the end of this run, were
Third Call
First of all, copy file AgB01000600t-sol.txt (generated by the
previous call to PUMA) to all the nodes of
your MPI Grid.
Finally, we can go to the third and last trial. If you look at the
output file
AgB01000600t-inf.txt of
the second call, you can see that the retrieved thicknesses are 100nm
and 600nm for the first and the second film,
respectively; the best quadratic error decreased to 3.800786e-05.
With this at hand, you can go the third and last trial.
For the third trial, submit to your MPI Grid, the following:
puma-par AgB01000600t 5 2 10 T 100 631 1621 1000000 3.800786e-05 9 100 100 1 631 631 1 600 600 1 631 631 1
where the bold font means, as before, which parameters were
changed from the previous call. Their meanings are
- We increased the number of iterations from 100000 to 1000000.
- We made
QUAD="previous quadratic error"=
3.800786e-05. This means that only thicknesses and constant
estimations with a quadratic error smaller than this one will be
saved.
- We considered the thicknesses as retrieved, with values 100nm and 600nm
for the first and the second film, respectively.
So we fix it by making
THICKNESSmin =
THICKNESSmax = 100, for the first film, and
THICKNESSmin = THICKNESSmax = 600, for the second film.
In this case, the THICKNESSstep is not considered at all
and it can take any value.
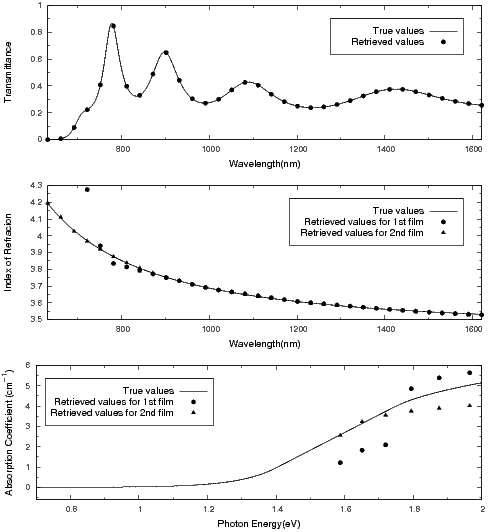
You can see the third output file
AgB01000600t-inf.txt3 or the
terminal output during this run.
The retrievals of the refractive indexes and the attenuation
coefficients at the end of this run, were
Remarks
The transmission T of the thin absorbing film deposited on a thick
transparent substrate must be a rate stated as a proportion of one
(something between zero and one) and not a percentage (between zero
and one hundred).
The transmission formula being used assumes that the substrate is
perfectly transparent. As a consequence of this limitation, the useful
spectral ranges 350-2000nm for glass, 1250-2600nm for crystalline silicon,
200-1500nm for crystalline quartz, 360-800nm for glass slides and
300-2600nm for borosilicate substrates must be retained in the
numerical experiments.
Everything we did in the examples above for transmittance,
can be repeated for reflectance data and for both
data (where both means to use transmittance and reflectance
simultaneously). The analogous input files to the ones used in the
one-film system example are
sigl0097r-dat.txt (for
reflectance data) and
sigl0097b-dat.txt (for
transmittance and reflectance data).
Related publications
- E. G. Birgin, I. Chambouleyron, and J. M. Martínez,
Estimation of optical constants of thin films using
unconstrained optimization, Journal of Computational Physics
151, pp. 862-880, 1999.
[pdf]
[ps]
The problem of estimating the thickness and
the optical constants of thin films using transmission data only
is very challenging from the mathematical point of view, and has a
technological and an economic importance. In many cases it
represents a very ill-conditioned inverse problem with many
local-nonglobal solutions. In a recent publication we proposed
nonlinear programming models for solving this problem.Well-known
software for linearly constrained optimization was used with
success for this purpose. In this paper we introduce an
unconstrained formulation of the nonlinear programming model and
we solve the estimation problem using a method based on repeated
calls to a recently introduced unconstrained minimization
algorithm. Numerical experiments on computer-generated films show
that the new procedure is reliable.
- M. Mulato, I. Chambouleyron, E. G. Birgin and J. M.
Martínez, Determination of thickness and optical
constants of a-Si:H films from transmittance data, Applied
Physics Letters 77, pp. 2133-2135, 2000.
[pdf]
[ps]
This work presents the first application of a
recently developed numerical method to determine the thickness and
the optical constants of thin films using experimental
transmittance data only. The new method may be applied to films
not displaying a fringe pattern and is shown to work for a-Si:H
layers as thin as 100 nm. The performance and limitations of the
method are discussed on the basis of experiments performed on a
series of six a-Si:H samples grown under identical conditions, but
with thickness varying from 98 nm to 1.2 mu m.
- I. Chambouleyron, S. D. Ventura, E. G. Birgin, and J.
M. Martínez, Optical constants and thickness
determination of very thin amorphous semiconductor films,
Journal of Applied Physics 92, pp. 3093-3102, 2002.
[pdf]
[ps]
This contribution addresses the relevant
question of retrieving, from transmittance data, the optical
constants and thickness of very thin semiconductor and dielectric
films. The retrieval process looks for a thickness that, subject
to the physical input of the problem, minimizes the difference
between the measured and the theoretical spectra. This is a
highly underdetermined problem but, the use of approximate -
though simple - functional dependences of the index of refraction
and of the absorption coefficient on photon energy, used as an a
priori information, allows surmounting the ill-posedness of the
problem. The method is illustrated with the analysis of
transmittance data of very thin amorphous silicon films. The
method allows retrieving physically meaningful solutions for films
as thin as 300 A. The estimated parameters agree well with known
data or with optical parameters measured by independent
methods. The limitations of the adopted model and the shortcomings
of the optimization algorithm are presented and
discussed.
- E. G. Birgin, I. Chambouleyron, and J. M. Martínez,
Optimization problems in the estimation of parameters of
thin films and the elimination of the influence of the
substrate, Journal of Computational and Applied Mathematics
152, pp. 35-50, 2003.
[pdf]
[ps]
In a recent paper, the authors introduced a
method to estimate optical parameters of thin films using
transmission data. The associated model assumes that the film is
deposited on a completely transparent substrate. It has been
observed, however, that small absorption of substrates affect in a
nonnegligible way the transmitted energy. The question arises of
the reliability of the estimation method to retrieve optical
parameters in the presence of substrates of different thicknesses
and absorption degrees. In this paper, transmission spectra of
thin films deposited on non-transparent substrates are generated
and, as a first approximation, the method based on transparent
substrates is used to estimate the optical parameters. As
expected, the method is good when the absorption of the substrate
is very small, but fails when one deals with less transparent
substrates. To overcome this drawback, an iterative procedure is
introduced, that allows one to approximate the transmittance with
transparent substrate, given the transmittance with absorbent
substrate. The updated method turns out to be almost as efficient
in the case of absorbent substrates as it was in the case of
transparent ones.
- E. G. Birgin, I. Chambouleyron, J. M. Martínez, and
S. D. Ventura, Estimation of optical parameters of very
thin films, Applied Numerical Mathematics 47, pp. 109-119,
2003.
[pdf]
[ps]
In recent papers, the problem of estimating
the thickness and the optical constants (refractive index and
absorption coefficient) of thin films using only transmittance
data has been addressed by means of optimization
techniques. Models were proposed for solving this problem using
linearly constrained optimization and unconstrained
optimization. However, the optical parameters of "very
thin" films could not be recovered with methods that are
successful in other situations. Here we introduce an optimization
technique that seems to be efficient for recovering the parameters
of very thin films.
- S. Ventura, E. G. Birgin, J. M. Martínez and
I. Chambouleyron, Optimization techniques for the estimation
of the thickness and the optical parameters of thin films using
reflectance data, Journal of Applied Physics 97, 043512, 2005.
[pdf]
[ps]
The present work considers the problem of estimating the thickness
and the optical constants (extinction coefficient and refractive
index) of thin films from the spectrum of normal reflectance
R. This is an ill-conditioned highly underdetermined inverse
problem. The estimation is done in the spectral range where the
film is not opaque. The idea behind the choice of this particular
spectral range is to compare the film characteristics retrieved
from transmittance T and from reflectance data. In the first part
of the paper a compact formula for R is deduced. The approach to
deconvolute the R data is to use well known information on the
dependence of the optical constants on photon energy of
semiconductors and dielectrics and to formulate the estimation as
a nonlinear optimization problem. Previous publications of the
group on the subject provide the guidelines for designing the new
procedures. The consistency of the approach is tested with
computer generated thin films and also with measured R and T
spectral data of an a-Si:H film deposited onto glass. The
algorithms can handle satisfactorily the problem of a poor
photometric accuracy in reflectance data, as well as a partial
linearity of the detector response.
- R. Andrade, E. G. Birgin, I. Chambouleyron, J. M. Martínez
and S. D. Ventura, Estimation of the thickness and the
optical parameters of several superimposed thin films using
optimization, Applied Optics 47, pp. 5208-5220, 2008.
[pdf]
[ps]
The Reverse Engineering problem addressed in the present research
consists in estimating the thicknesses and the optical parameters
of two thin films deposited on a transparent substrate using only
transmittance data through the whole stack. To the present author's
knowledge this is the first report on the retrieval of the optical
constants and the thickness of multiple film structures using
transmittance data only. The same methodology may be used if the
available data correspond to normal reflectance. The software used
in this work is freely available through the PUMA Project web page
(http://www.ime.usp.br/~egbirgin/puma/).




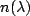 and
and 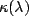 . We recommend you to use
3000 for the first trial, 5000 for the second trial, and 50000 for
the last one.
. We recommend you to use
3000 for the first trial, 5000 for the second trial, and 50000 for
the last one.






