


Next: Bibliografia
Up: MAC 747 Geometria Computacional
Previous: Critério de avaliação
Alguns dos tópicos que pretendemos cobrir nesta disciplina são:
fechos convexos; problemas de proximidade; partições convexas; busca
geométrica; e problemas de intersecção.
Abaixo encontra-se uma breve descrição de alguns problemas que
estudaremos nesta disciplina.
O Problema do par mais próximo (The closest pair problem)
Dados n pontos queremos encontrar dois cuja distância entre eles é mínima.
Uma aplicação prática deste problema é em controle de tráfego aéreo: os dois
aviões que estão em maior perigo de colisão são aqueles que estão mais
próximos. Este problema pode ser resolvido facilmente em O(dn2) onde d é
a dimensão do espaço. O problema do par mais próximo pode ser resolvido por
um algoritmo do tipo divisão-e-conquista em tempo 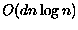 (cf. Capítulo
5 de [19]) .
(cf. Capítulo
5 de [19]) .
Fecho convexo de um conjunto de pontos
Dados n pontos queremos encontrar o fecho convexo desses pontos. Uma
aplicações práticas deste problema se encontra em robótica. Se o
fecho convexo de um robô não colide com obstáculos então o robô também
não colide. Segundo O'Rourke (cf. [17], pg. 80) talvez o
primeiro artigo na área de geometria computacional tenha sido sobre
fechos convexos.
Nos anos 60 uma aplicação da Bell Labs necessitava computar o fecho convexo
de aproximadamente 10.000 pontos no plano e os algoritmos de
complexidade de tempo O(n2) eram muito lentos. Tendo esse problema
como motivação, no começo do anos 70, Graham [10] desenvolveu
o primeiro algoritmo de complexidade de tempo 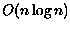 .
O fecho
convexo também pode ser construído em
.
O fecho
convexo também pode ser construído em 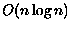 por um algoritmo de
divisão-e-conquista (cf. Capítulo 3 de [PreSha]).
por um algoritmo de
divisão-e-conquista (cf. Capítulo 3 de [PreSha]).
Triangularização de polígonos
Dado um polígono P queremos adicionar
o maior número possível de diagonais (que não se cruzem) a P de tal
forma que o interior do polígono fique particionado em triângulos.
Chazelle [1] desenvolveu um algoritmo linear para
este problema.
Um algoritmo para triangularizar polígonos pode ser utilizado em
problemas do tipo Art Gallery (cf. [16]). Imagine
que as salas de uma galeria de arte formem um polígono. Qual é o menor
número de guardas que são necessários para tomarem conta das salas.
Estamos consideramos que cada guarda fique parado em um local da
galeria.
Partição de polígonos
Além de algoritmos eficientes para
particionar um polígono em triângulos, também é de interesse o
desenvolvimento de algoritmos
que particionem um polígono em (digamos) polígonos monótonos,
trapezóides e polígonos convexos. Uma motivação para particionar um
polígono em polígonos convexos é reconhecimento de caracteres: um
caractere pode ser representado como um polígono particionado em
partes convexas.
Diagramas de Voronoi
Dado um conjunto S de n pontos no plano queremos
determinar para cada ponto p em S qual é a região V(p) dos
pontos do plano que estão mais perto de p do que de qualquer outro
ponto em S. As n regiões V(p) formam uma partição do plano
chamada de Diagrama de Voronoi.
Imagine uma vasta floresta contendo vários pontos de observação de
incêndio. O conjunto das árvores que estão mais próximas de um
determinada posto p determina a região V(p) das árvores que são de
responsabilidade de ponto p.
O diagrama de Voronoi de um conjunto de n pontos pode ser contruído
em 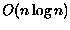 por um (complicado) algoritmo do tipo
divisão-e-conquista (cf. [21]). Em 1985,
Fortune [9] desenvolveu um algoritmo de varredura
(plane-sweep algorithm) muito elegante e simples cuja
complexidade de tempo é
por um (complicado) algoritmo do tipo
divisão-e-conquista (cf. [21]). Em 1985,
Fortune [9] desenvolveu um algoritmo de varredura
(plane-sweep algorithm) muito elegante e simples cuja
complexidade de tempo é 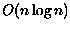 .
.
Triangularização de Delaunay
O dual geométrico (usando retas) de
um diagrama de Voronoi para um conjunto S de pontos forma uma
triangularização do conjunto S, chamada de triangularização
de Delaunay. A triangularização de Delaunay tem várias
propriedades geométricas interessantes, por exemplo, ela contém todas as ``árvores
geradoras mínimas'' de S (cf. Capítulo 6 de [19]).



Next: Bibliografia
Up: MAC 747 Geometria Computacional
Previous: Critério de avaliação
1999-04-26