MAC 499 Trabalho de Formatura Supervisionado

A disciplina MAC 499 - Trabalho de Formatura Supervisionado é disciplina obrigatória do currículo novo do BCC, com 16 créditos-trabalho. A disciplina tem como pré-requisitos duas disciplinas entre MAC422 Sistemas Operacionais, MAC426 Bancos de Dados, MAC332 Engenharia de Software, MAC328 Algoritmos em Grafos. Não será permitido ao aluno fazer as disciplinas sem possuir os pré-requisitos, nem mesmo cursá-los em paralelo.

O aluno poderá escolher entre um dos seguintes modos de trabalho de formatura:

Estágio supervisionado
Iniciação científica

O aluno matriculado em MAC499 deve procurar no início do semestre um professor para ser seu supervisor.
Estou disposto a supervisionar ambos os modos de trabalho. Abaixo encontra-se uma listas de possíveis temas de iniciação científica que gostaria de supervisionar. A medida que eu me lembrar ou me vierem a cabeça outros temas eu escreverei nesta página.
Por favor, se você deseja que eu supervisione o seu estágio ou estiver interessado em saber mais sobre algum dos temas abaixo me procure ou mande um mail .
Para aqueles que estiverem interessados em fazer pós-graduação gostaria de avisar que alguns dos temas abaixo podem ser, no final da iniciação, facilmente trasformados em um projeto de dissertação mestrado.
[Especificação do trabalho de formatura - MAC499, Programa de MAC 499]

Caminhos mínimos em grafos não-dirigidos

M. Thorup desenvolveu um algoritmo liner O(m) para o problema do caminho mínimos em grafos não-dirigidos. O problema do caminho consiste (the single source shortest paths problem): dados: um grafo não-dirigido G=(V,E) com comprimentos positivos em suas arestas e um vértice s; encontrar: caminhos mínimos entre s e cada um dos vértices de G (uma árvore de caminhos mínimos com raiz s).

Desde 1959 todos os desenvolvimentos teóricos para o problema do caminho mínimo para grafos dirigidos e não dirigidos foram baseados no Algoritmo de Dijkstra: visitar os vértices em ordem decrescente de distância tentativa até s. Portanto, qualquer implementação do Algoritmo de Dijkstra ordena os vértices de acordo com as suas distâncias até s. Entretanto, não sabemos ordenar em tempo linear.

M. Thorup propôs uma algoritmo determinístico que em tempo e espaço linear resolve o problema do caminho mínimo para grafos não-dirigidos com comprimentos inteiros positivos em suas arestas. O algoritmo evita o gargalo de ordenação através da construção de uma estrutura de dados especial.

Eu gostaria de estudar este algoritmo e se possível ver uma implementação dele. A implementação poderá envolver CWEB, SGB e LEDA:

D.E. Knuth, The Stanford GraphBase: A platform for combinatorial computing, Addison Wesley, New York, 1993.
D.E. Knuth, and Silvio Levy, The CWEB System of Structured Documentation, Addison Wesley, Reading, Massachusetts, 1994.
K. Mehlhorn and St. Näher, The LEDA Platform of Combinatorial and Geometric Computing, Cambridge Press, 2000.

M. Thorup, Undirected single source shortest paths with positive integer weight in linear time (postscript), manuscrito, 1999.

Algoritmos probabilísticos

Eu tenho um livro que estou com muita vontade de estudar:

Randomized Algorithms
by Rajeev Motwani and Prakhabar Raghavan
Cambridge University Press, 1995

Vamos traduzir Randomized Algorithms para "algoritmos probabilísticos", já que em português "algoritmos aleatórios" tem um ar de "algoritmos feitos-nas-coxas".

Existe uma coisa chamada análise probabilística de algoritmos, que, tipicamente e grosseiramente, consiste em pegarmos um algoritmo que desejamos analisar e supormos uma distribuição de probabilidade sobre o conjunto de possíveis instâncias para o problema que este algoritmo resolve. Depois disto podemos, por exemplo, começar a falar do `tempo esperado' (ou `tempo médio') gasto pelo algoritmo. Talvez o exemplo mais conhecido deste tipo de análise é a análise probabilística do Quicksort, onde mostra-se que o tempo esperado gasto pelo algoritmo é O(n log n) (apesar do seu pior caso ser quadrático), o que, de certa forma, explica a eficiência do algoritmo na prática.

Em um algoritmo probabilístico existe algum passo onde `uma moeda e jogada' ou `um número é sortedado'. Novamente considere o exemplo do Quicksort, uma versão probabilística deste algoritmo poderia, no início de cada iteração, sortear o elemento pivô que será usado pelo algoritmo de partição. Já que o algoritmo tem esse componente aleatório temos que o tempo gasto pelo algoritmo ou mesmo a sua resposta passam a ser variáveis aleatórias.

Aleatorização (seja lá o que for isto) parece ser um instrumento muito poderoso para o desenvolvimento de algoritmos. Por exemplo, observe que um usuário maldoso pode construir uma instância onde o Quicksort determinístico gasta tempo quadrático. Já este mesmo usuário maldoso não tem como determinar uma instância que faz com que o Quicksort probabilístico gaste tempo quadrático.

Aleatorização também é uma ferramenta usada para tornar algoritmos mais eficientes (pelo menos probabilisticamente).

Eu gostaria de estudar este livro e, quem sabe, tentar fazer um estudo experimental de algum desses algoritmos probabilísticos.

Caminhos disjuntos em grafos não-dirigidos planares

Considere o seguinte problema:

dados:

um grafo planar G=(V,E);
pares (r₁ , s₁) , (r₂ , s₂) , ... , (r_k , s_k) , de vértices de G;

encontrar:

caminhos disjuntos nos vértices P₁ , P₂ , ... , P_k em G, onde P_i é um caminho de r_i a s_i para i=1 , 2 , ... , k.
Este problema é NP-difícil (ou seja, muita gente acredita que não existe um algoritmo de complexidade de tempo polinomial para o problema). Em alguns casos especiais, entretanto, existe um algoritmo polinomial para o problema.

A. Schrijver propôs um algoritmo polinomial para uma variante do problema acima, o chamado disjoint homotopic paths problem. A linguagem usada para descrever a variante e o respectivo algoritmo é a de homotopia (não precisa saber o que é isto, em 5 minutos é possível dar a idéia do que se trata). Eu gostaria de dar uma estuda neste algoritmo (e ver ser dar para melhorar a sua complexidade -- mas isto já é o outra coisa).

Caminhos disjuntos em grafos dirigidos planares

A. Schrijver mostrou que para k fixo o seguinte problema pode ser resolvido em tempo polinomial:

dados:

um grafo dirigido D=(V,A);
pares (r₁ , s₁) , (r₂ , s₂) , ... , (r_k , s_k) , de vértices de D;

encontrar:

k caminhos disjuntos nos vértices P₁ , P₂ , ... , P_k em D, onde P_i é um caminho de r_i a s_i para i=1 , 2 , ... , k.
Este problem é NP-difícil se não fixarmos k. Desta vez, a linguagem usada para descrever o algoritmo é a de grupos livres (seja lá o que for isto; tem algo a haver com álgebra). Tem alguém por ai que gostaria de estudar o artigo comigo ou dar uma olhada nele ;-)?

Coleção máxima de árvores geradoras disjuntas

O problema aqui é: dado: um grafo não-dirigido conexo G; encontrar: uma coleção máxima de árvores geradoras disjuntos de G (ou seja, nenhuma aresta de G pode aparecer em mais do que uma árvore da coleção e a coleção deve ter o maior número possível de árvores).

Existe um algoritmo polinomial bem pé no chão para este problema e seria muito bacana se o algoritmo fosse implementado. A implementação poderá envolver CWEB, SGB e LEDA:

Despois de implementado eu acharia muito legal ver um algoritmo polinomial para um problema que é uma extensão deste problema da coleção máxima de árvores geradoras disjuntas. Mas isto já e outra estória ...

Funções submodulares

Permitam-me eu dar mais uma voada ... Talvez seja difícil de acreditar, mas este tópico tem a haver com o tópico anterior.

Vocês devem estar se perguntando "Que katissu é uma função submodular e para que serve?".

Uma função submodular sobre um conjunto finito V é uma função f definida sobre a coleção de subconjuntos de V tal que

f(Y) + f(Z) >= f(Y intersecção Z) + f(Y união Z)
para todo Y, Z subconjuntos de V.
Submodularidade aparece em muitos teoremas e problemas em combinatória e freqüentemente tem um papel essencial em uma prova ou em um algoritmo (método guloso para encontrar uma árvore geradora mínima, por exemplo).
Muitos dos estudos em combinaória envolvendo uma função submodular seguem o seguinte padrão. Tome algum resultado clássico em teoria dos grafos (por exemplo o Teorema do Fluxo Máximo e Corte Mínimo), e troque certas funções que aparecem no problema (ou a função objetivo ou as retrições) por uma funções submodulares. Muitas vezes a general\ ização obtida do teorema original permanece válida.
Um exemplo de função submodular é a função capacidade de um corte. Seja D=(V,A) um grafo dirigido e c uma função `capacidade' dos arcos A de D nos inteiros não-negaticos. Definamos a função cap(X), para todo subconjunto X dos vértices V de D, como sendo a soma das capacidades dos arcos que vão de X para V - X. A função cap é um exemplo de função submodular.
Tem alguém por ai que gostaria de estudar essas funções e, principalmente, os algoritmos para minimizar uma função submodular? Dizemos que um subconjunto X de V minimiza uma função submodular f se

f(X) = min{ f(Y) | Y é subconjunto de V}
Por exemplo, minimizar a função cap definida acima é o mesmo que encontrar um corte de capacidade mínima no grafo D.

Triangularização de peso mínimo

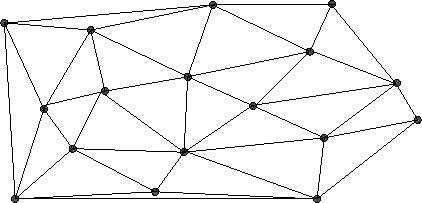
O Problema da Triangularizaçào de Peso mínimo é um exemplo de problema para o qual um algoritmo que faz decisões ótimas a cada passo (algoritmo guloso), não fornece uma solução que é ótima globalmente. Dado um conjunto de pontos no plano, uma triangularização é um conjunto maximal de segmentos de reta ligando os pontos tal que dois a dois os segmentos não se intersectam ``propriamente'' (veja Figura abaixo). O peso de uma triangularização é a soma dos comprimentos dos segmentos. Dado um conjunto de pontos no plano, o Problema da Triangularização de Peso Mínimo é o problema de encontrar, entre todas as triangularizações do conjunto de pontos dado, uma cujo peso seja mínimo.

Figura: Uma triangularização de um conjunto de pontos.
$\begin{figure} \begin{center} \epsfbox{lista5ex4.eps} \end{center}\end{figure}$

A complexidade do Problema da Triangularização de Peso Mínimo está aberta desde 1975 quando foi mencionado por Shamos e Hoey. Não se conhece algoritmo polinomial para resolver este problema e também não se sabe se o problema é NP-difícil (ou se ambos ;-)). Até bem pouco tempo o melhor algoritmo de tempo polinomial conhecido produzia uma triangularização que, no pior caso, é O(log n) vezes o peso de uma triangularização de peso mínimo. Uma triangularização gulosa (greedy) de um conjunto de pontos é uma triangularização produzida pelo seguinte algoritmo:

Algoritmo Guloso(S)
Entrada: Um conjunto finito S de pontos no plano.
Saída: Uma triangularização de S.

T := vazio;

L := o conjunto de todos os segmentos ligando pares de pontos de S;

while L é não-vazia do

Seja e um segmento em L de menor comprimento;
Remova e de L;
if (e não intersecta os segmentos em T) então Insira e em T;

endwhile

O Algoritmo Guloso escolhe uma aresta de comprimento mínimo em cada passo. (Exercício: Construa um instância S para o algoritmo tal que S tem 5 pontos e a triangularização gulosa de S não é uma triangularização de peso mínimo.)
Demonstra-se que a triangularização gulosa produz, no pior caso, uma triangularização que é "\theta(n)" vezes mais pesada que uma triangularização ótima.
Bem, vamos ao ponto. Mais recentemente, foi bolado um algoritmo que produz uma triangularização que, no pior caso, é O(1) vezes o peso de uma triangularização de peso mínimo. (Não acheia a referência, ainda preciso encontrá-la.) Eu gostaria de estudar este algoritmo e talvez implementá-lo para fazer uns testes.
O Cassio Polpo de Campos e o Eduardo Freitas andaram estudando este problema durante a iniciação científica orientada pelo Prof. Carlos Eduardo Ferreira (Carlinhos).
Mais sobre este e outros problemas em geometria computacional pode ser encontrado em Geometria Computacional no DCC-USP.

Coelho's Home Page.

Last modified: Wed Feb 16 09:58:10 BRST 2000