MAC0328 Algoritmos em Grafos

Sexto Exercício-Programa. Fluxos

Objetivos

  1. Implementar um algoritmo para o problema do fluxo máximo: método dos caminhos de aumento de Ford e Fulkerson [7].
  2. Uso de busca em largura para obtenção dos caminhos de aumento, como sugerido por Edmonds e Karp [5]. Veja também busca em largura versão 2001.

Descrição

Introdução

Este exercício-programa consiste na implementação do método dos caminhos de aumento que recebe um grafo com capacidades nos arcos e dois vértices r e s e devolve um fluxo de r a s de intensidade máxima e um separador de capacidade mínima.

O seu programa C (documento CWEB) deve chamar-se fluxo.c (fluxo.w, repectivamente). O programa deve utilizar a biblioteca do SGB para a manipulação de grafos.

Nota. A descrição do método de dos caminhos de aumento é baseada no livro:

R.E. Tarjan, Data Structures and Network Algorithms, CBMS-NSF Regional Conference Series in Applied Mathematics, Philadelphia, Pennysylvania, 1983.


Fluxos

A capacidade a->cap de um arco a de um grafo é um número inteiro não-negativo.

Sejam g um grafo com capacidades nos arcos e r e s vértices de g. Uma atribuição de um número inteiro não-negativo a->flx a cada arco a de g é um fluxo de r a s se

  1. a->flx <= a->cap para todo arco a; e
  2. v->flxs == v->flxe para todo vértice v distinto de r e s, onde v->flxs denota o somatório de a->flx para todo arco a que sai de v e v->flxe denota o somatório de a->flx para todo arco a que entra em v.
A segunda propriedade acima é conhecida pelo nome de lei de conservação do fluxo ou ainda como lei de Kirchhoff.

Um grafo com capacidades nos arcos junto com dois vértices especiais é muitas vezes chamado de uma rede (network). Em outras palavras, uma rede é um quarteto (g, cap, r, s).

A intensidade ou valor de um fluxo flx de r a s é o número

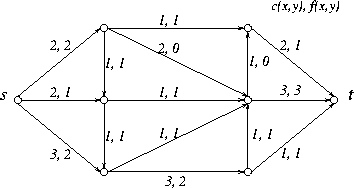
val(flx) == r->flxs - r->flxe.
Em geral, mas nem sempre, r->flxe == 0. A figura abaixo mostra um fluxo de valor 5.


  
Figura 1: Rede com um fluxo maximal de s a t. O primeiro número próximo de cada arco representa a sua capacidade e o segundo representa o fluxo neste arco. [O vértice s na figura é aquele que no texto é chamado de r e o vértice t é o vulgo s.]
\begin{figure} \begin{center} \epsfbox{fluxo1.eps} \end{center}\end{figure}

PROBLEMA (do fluxo máximo): Dado um grafo com capacidades nos arcos e vértices r e s, encontrar um fluxo de r a s de intensidade máxima.

Separadores

O principal resultado em Ford e Fulkerson [7] é o famoso Teorema do Fluxo Máximo e Corte Mínimo (the max-flow min-cut theorem--independentemente provado por Elias, Feinstein e Shannon [6] e Kotzig [?]). Antes de tratarmos desse teorema necessitamos alguns conceitos.

Um separador de rs é um conjunto X de vértices tal que r está em X e s está fora de X. A capacidade de um conjunto X de vértices é o número

cap(X)
que é soma das capacidades dos arcos que saem de X. [O conjunto dos arcos que saem de X é dito corte determinado por X.] Uma observação fácil de verificar é o lema a seguir.

Lema 1 (da dualidade): Se flx é um fluxo de r a s e X é um separador de rs, então

val(flx) <= cap(X).
Ademais, se val(flx) == cap(X), então flx é um fluxo de intensidade máxima e X é um separador de capacidade mínima.

Demonstração. Pela definição de valor de um fluxo tem-se que 

         val(flx) == flxs(r) - flxe(r) 
                  == flxs(r) - flxe(r) + flxs(X-{r}) - flxe(X-{r})
                  == flxs(X) - flxe(X)
                  <= flxs(X)
                  <= cap(X).
A primeira igualdade segue da lei de conservação do fluxo.

A solução do problema do fluxo máximo mostrará que a recíproca da segunda parte do lema acima também vale. O algoritmo que resolve o problema do fluxo máximo tem a seguinte especificação: ao receber vértices r e s, o algoritmo devolve

um fluxo flx e um separador X de rs tais que val(flx) == cap(X).

Grafos residuais

Seja g um grafo com capacidade nos arcos e flx um fluxo de um vértice r a um vértice s. Associamos a g e flx um grafo h com capacidade nos arcos. O grafo h é definido da seguinte maneira:

  1. h tem os mesmo vértices de g;
  2. os arcos de g são arcos de h; e
  3. para cada arco de ade g, o grafo h tem ainda um arco a->irmão tal se a vai de u a v, entao a->irmão vai de v a u.
Para cada arco a de g, se a' = a->irmão, então defina a'->irmão como sendo a. A capacidade a->res de um arco de h é
a->cap - a->flx
se a é arco de g ou
a->irmão->flx
se a->irmão é um arco de g.

O grafo h é dito grafo residual para g e flx.

Caminhos de aumento

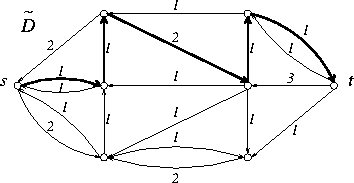
Suponha que h é o grafo residual para g e flx. A capacidade residual res(P) de um caminho P em h é a menor capacidade de um arco em P.

Um caminho em h com ponta inicial em r e de capacidade residual positiva é dito um caminho alternante. Um caminho de aumento (augmenting path) é um caminho alternante com ponta final em s.

  
Figura 2: Grafo residual para o grafo e fluxo da Figura  1. Os arcos de capacidade nula não estão sendo mostrados na figura. Um número próximo a um arco indica a sua capacidade. Os arcos mais grossos na figura mostram um caminho de aumento de capacidade residual 1.
\begin{figure} \begin{center} \epsfbox{residual.eps} \end{center}\end{figure}

Lema 2 : Seja flx é um fluxo de r a s e P é um caminho de aumento. Para cada arco a de g defina:

a->flx' := a->flx + res(P), se a é um arco em P;
a->flx' := a->flx - res(P), se a->irmão é um arco em P; e
a->flx' := a->flx, em caso contrário;
A atribuição do valor a->flx' a cada arco a de g é um fluxo de r a s de intensidade val(flx) + res(P).

Demonstração. Exercício. $\mbox{val}(f') = \mbox{val}(f) + res(P)$ . (Veja Figura  3.)

  
Figura: Grafo da Figura  1 com o fluxo flx' obtido a partir do fluxo flx e do caminho de aumento na Figura  3. O conjunto S é um separdor de capacidade mínima.
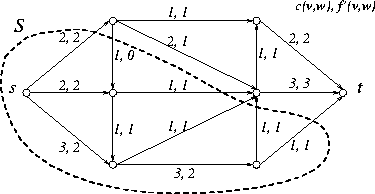\begin{figure} \begin{center} \epsfbox{fluxo2.eps} \end{center}\end{figure}

Lema 3 : Se flx é um fluxo de r a s e não existe um caminho de aumento, então existe um separador X de rs tal que

val(flx) == cap(X).

Demonstração. Seja X o conjunto do vértices que são terminos de caminhos alternantes. Como não existe caminho de aumento, r está em X e s está fora de X. Assim, X é um separador de rs. Ademais, da definição de X segue que 

        a->flx == 0                              (1)
para cada arco a que entra em X e 
        a->flx == a->cap                         (2)
para cada arco a que sai de X. Portanto, 
        val(flx) == flxs(r) - flxe(r) 
                 == flxs(r) - flxe(r) + flxs(X-{r}) - flxe(X-{r})
                 == flxs(X) - flxe(X)
                 == flxs(X)              
                 == cap(X).
A quarta igualdade é devida a (1) e a quinta igualdade é devida a (2).

Teorema do fluxo máximo e corte mínimo

O fato central desta parte da disciplina é o seguinte teorema devido a Ford e Fulkerson [7], Elias, Feinstein e Shannon [6] e Kotzig [?]. (Nesta penúltima referência os autores afirmam que o resultado era conhecido na área de communication theory.)

Teorema 1 (do fluxo máximo e corte mínimo):   A maior intensidade de um fluxo de r a s é igual a menor capacidade de um separador de rs.

Demonstração. O teorema é conseqüência dos lemas 1, 2 e 3.

Em um artigo de 1o. de janeiro de 1955, Dantzig e Fulkerson [1955] mostraram que o Teorema do Fluxo Máximo e Corte Mínimo também pode ser deduzido a partir do teorema de dualidade de programação linear e em um artigo de 1o. de abril de 1955 Fulkerson e Dantzig [1955] propuseram um método computacional simples para o problema do fluxo máximo baseado no método simplex.

Método dos caminhos de aumento (Ford e Fulkerson  [7])

O método recebe um grafo g com capacidade nos arcos e dois vértices r e s e devolve um fluxo de r a s de intensidade máxima e um separador de rs de capacidade mínima. Cada iteração começa com um fluxo de r a s. A primeira iteração começa com o fluxo zero em todos os arcos (zero flow). Cada iteração consiste em repetir o seguinte passo até obter um fluxo f sem um caminho de aumento:
PASSO DE AUMENTO (AUGMENTING STEP): Encontre um caminho de aumento P para o fluxo corrente. Aumente o valor do fluxo fornecendo res(P) unidades de fluxo `através' do caminho P.
Dado um fluxo máximo flx um corte mínimo pode ser encontrado em tempo O(n+m) fazendo-se busca no grafo residual para g e flx.

Suponha que a capacidade dos arcos é inteira. Então o método dos caminhos aumentantes aumenta o valor do fluxo de pelo menos 1 em cada iteração. Logo o método encontra um fluxo máximo depois de no máximo min{cap(X) : X é um separador de rs} passos aumentantes. Além disso o fluxo máximo devolvido pelo algoritmo será inteiro. Dizemos que um fluxo flx é inteiro se a->flx é um número inteiro para cada arco a.

Teorema 2 (da integralidade): Se a->cap é um número inteiro para cada arco a, então existe um fluxo máximo inteiro. Ademais, o método dos caminhos de aumento devolve um fluxo máximo inteiro.

O teorema da integralidade também é conseqüência do Método Simplex de Dantzig [2].

Infelizmente se as capacidades forem inteiros muito grandes o método dos caminhos aumentantes pode fazer muitos passos aumentantes. O número de passos aumentantes do método depende de

C := max{a->cap : a é um arco}
Portanto para capacidades inteiras o método é um algoritmo pseudo-polinomial. (Para ser polinomial o número de passos aumentantes necessita ser um polinômio em m, n e log(C).)
  
Figura: Um exemplo maldoso para o método dos caminhos de aumento. (a) grafo dado. (b) fluxo após aumentarmos através do caminhos (s,a,b,t). (c) fluxo após aumentarmos através do caminho (s,b,a,t). Depois de 2 milhões de passos de aumento, através dos caminhos (s,a,b,t) e (s,b,a,t) alternadamente, o fluxo será máximo.
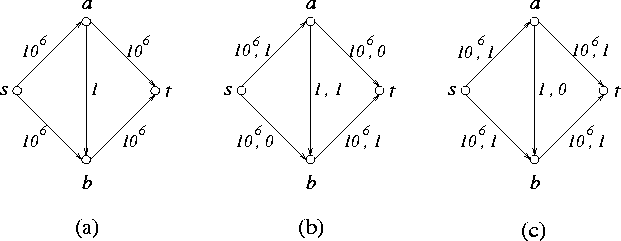\begin{figure} \begin{center} \epsfbox{pseudo.eps} \end{center}\end{figure}

É desejável um algoritmo onde o número de passos aumentantes seja uma função polinomial de n e m e não dependa de C (strongly polynomial-time algorithm). Outro método sugerido por Edmonds e Karp [5] é sempre escolher um caminho aumentante com o menor número possível de arcos. Esse método é mais eficiente se aumentarmos o fluxo através de caminhos de mesmo comprimento simultaneamente (cf. Dinits [4]).

Teorema 3 : Se os passos de aumento são feitos através de caminhos de com um número mínimo de arcos, então o método dos caminhos de aumento pára depois de (n-1)m passos de aumento e encontra um fluxo máximo em tempo O(nm2).

Observação. Se as capacidades dos arcos forem irracionais o método pode não parar. Pior que isso, pode ocorrer que a seqüência das intensidades do fluxos obtidos convirga para um valor bem diferente do valor do fluxo máximo! Note que essa seqüência certamente converge já que ela é estritamente crescente e limita; a capacidade do corte mínimo é um limitante superior. Um exemplo maldoso de onde isso ocorre pode ser encontrado em Papadimitriou e Steiglitz [10] páginas 124-128.

Comportamento do seu programa

Neste exercício-programa você implementará o método dos caminhos aumentantes de Ford e Fulkerson [7] para encontrar um fluxo máximo e um corte mínimo em uma rede dada. Os caminhos de aumento devem ser obtidos usando-se a sugestão de Edmonds e Karp [5], isto é, encontre caminhos de aumento com o menor número possível de arcos.

O programa deve receber como entrada, na linha de comando, o nome de um arquivo .gb contendo a representação de um grafo com capacidades nos seus arcos, e os nomes de dois vértices distintos origem e destino e deve fornecer como saída o valor do fluxo máximo do vértice origem ao vértice destino. A saída do seu programa deve ser enviada para a saída padrão (stdout).

meu_prompt> fluxo

Como saída o programa deverá imprimir uma mensagem explicando como o programa deve ser chamado.

meu_prompt> fluxo "nome do vértice origem" "nome do vértice destino" nome_do_grafo[.gb]

O seu programa deve determinar o fluxo de intensidade máximo no grafo nome_do_grafo do vértice de nome "nome do vértice origem" ao vértice de nome "nome do vértice destino" e um separador de capacidade mínima. Como vocês já sabem as aspas são importantes para a determinação correta dos nomes dos vértices, por exemplo
meu_prompt> fluxo  "Sorocaba, SP" "Sao Paulo, SP" cidades.gb
Opcionalmente, se o usuário usar a opção -v, o programa deve:
  1. listar o fluxo em cada um dos arcos do grafo;
  2. listar os vértices em um subconjunto X de vértices, tal que cap(X) == val(flx).
O conjunto X define um separador de rs de capacidade igual a intensidade do fluxo, provando que o fluxo é máximo e o separador tem capacidade mínima.

Exemplo: 

meu_prompt> fluxo -v "Sorocaba, SP" "Sao Paulo, SP" cidades.gb

O seu programa deve prever pelo menos os seguintes casos, informando o fato ao usuário com uma mensagem conveniente:

  1. O programa é chamado com parâmetros incorretos;
  2. O grafo não é encontrado;
  3. Algum dos vértices (origem ou destino) não é encontrado;

Detalhes de implementação

Para encontrar os caminhos de aumento, ou seja, caminhos de r a s no grafo residual para o fluxo corrente, como sugerido por Edmonds e Karp, utilize busca em largura.

O algoritmo precisa de uma estrutura de dados auxiliar que permita as operações INICIALIZA-FILA, PRIMEIRO-DA-FILA, INSIRA-NA-FILA, e REMOVA-DA-FILA. A fila deverá ser representada como uma lista linear (vetor) de apontadores para Vertex.

O campo len de cada arco a guardará a sua capacidade a->cap ou a sua capacidade residual a->res se o arco a não for um arco do grafo original g, mas apenas de grafo residual h. 

       #define cap len
Assim, a -> cap é a capacidade do arco a.

Campos de um vértice

Assim que o vértice s for alcançado por um caminho alternante P, o seu programa deverá ser capaz de determinar todos os arcos nesse caminho para que o fluxo nesses arcos e nos arcos do grafo original g, sejam alterados comvenientemente de res(P) (capacidade residual do caminho) unidades de fluxo. Para isto sugiro que cada vértices tenha os seguintes campos. 

       #define pred  z.A

v->pred é um apontador para o arco a da árvore de busca em largura tal que a->tip == v. 

       #define cap_res y.I

v->cap_res é a menor capacidade residual de uma arco no caminho de r a v na árvore de busca em largura. Isto significa que quando um caminho de aumento P é encontrado vale que 

       res(P) == s->cap_res.

Campos de um arco

Podemos representar ambos, o grafo dado g e o grafo residual h para g e flx, em um mesmo grafo no SGB.

Para cada arco do grafo original crie um arco reverso e chame estes dois arcos de irmãos. Assim, se a é um arco de u a v então a->irmão é um arco de v a u. Exatamente um dentre a e a->irmão é arco do grafo g e ambos são arcos no grafo residual h. (que também pode ser arco do grafo residual, dependendo se cap - fluxo é ou não maior que zero) e o outro é um arco apenas do grafo residual (com capacidade residual possívelmente nula).

Para cada arco nós necessitamos de:

  1. um campo indicando o fluxo no arco, caso o arco seja um arco do grafo g;
  2. um campo do arco que aponta para o seu arco irmão;
  3. um campo que aponta para o vértice de onde este arco está saindo.

Sugiro que façamos o seguinte (estou apenas sugerindo...).

  1. Usemos o campo a.I de cada arco para guardar o fluxo no arco e determinar se o arco é um arco do grafo original. 
           #define flx  a.I
    a->fluxo guarda o fluxo corrente no arco a, caso a seja um arco do grafo g. Se a for apenas um arco do grafo h, então a->flx guarda, digamos, -1.
  2. Usemos o campo a.A de cada arco para apontar para o seu arco irmão. 
          #define irmão b.A
    a->irmão aponta para o arco irmão do arco a. Portanto, a->irmão->irmão é um apontador para o próprio arco a.
  3. Para saber de qual vértice um arco a está saindo podemos `perguntar' ao seu irmão. 
          #define início irmão->tip
    a->início aponta para o vértice de onde o arco a está saindo. Portanto, a->início e a->tip são as pontas do arco a.

Perguntas e respostas

Pergunta. Como saber se um arco a é um arco do grafo g?

Resposta. Se a->flx é maior ou igual a zero, então a é um arco do grafo g.

Pergunta. Como saber a capacidade a->res de um arco a do grafo residual h?

Resposta. O valor de a->res é mantido implicitamente. Existem duas possibilidades:

  1. a->flx é maior ou igual a zero. Neste caso a é um arco do grafo g e 
         a->res == a->cap - a->flx
    Assim, a->res indica a quantidade de fluxo que ainda pode ser enviada através de a.
  2. a->flx é negativo. Nesta caso sabemos que a não é um arco do grafo g. O arco a pertence apenas grafo residual h (como foi definido na parte teórica) e portanto 
         a->res == a->irmão->flx

Você deve considerar as respostas às perguntas acima para adaptar a busca em largura que será feita no grafo h. Bem, acho que por enquanto é só.

Divirtam-se!

Grafo de cidades brasileiras

O professor José Augusto fez programas para criar grafos (.gb) de cidades brasileiras. Veja os dados, grafos e os programas em http://www.ime.usp.br/~coelho/grafos/sgb/cidades/. Você pode usar este grafo de cidades brasileiras para brincar com o seu programa.

Módulo GB_MILES

O módulo GB_MILES (gb_miles.w) do SGB contém a subrotina miles que você pode usar para testar e brincar com o seu programa bellman.

Copiado do arquivo gb_miles.w:

The subroutine call

miles(n,north_weight,west_weight,pop_weight,max_distance,max_degree,seed)

constructs a graph based on the information in miles.dat. Each vertex of the graph corresponds to one of the 128 cities whose name is alphabetically greater than or equal to `Ravenna, Ohio' in the 1949 edition of Rand McNally & Company's Standard Highway Mileage Guide. Edges between vertices are assigned lengths representing distances between cities, in miles. In most cases these mileages come from the Rand McNally Guide, but several dozen entries needed to be changed drastically because they were obviously too large or too small; in such cases an educated guess was made. Furthermore, about 5% of the entries were adjusted slightly in order to ensure that all distances satisfy the ``triangle inequality'': The graph generated by miles has the property that the distance from u to v plus the distance from v to w always exceeds or equals the distance from u to w.

The constructed graph will be ``complete''---that is, it will have edges between every pair of vertices---unless special values are given to the parameters max_distance or max_degree. If max_distance!=0, edges with more than max_distance miles will not appear; if max_degree!=0, each vertex will be limited to at most max_degree of its shortest edges.

Um exemplo de uso da função miles pode ser encontrado no módulo MILES_SPAN (miles_span.w), como mostrado abaixo. 

#include "gb_miles.h" /* the |miles| routine */
[...]
main(argc,argv)
  int argc; /* the number of command-line arguments */
  char *argv[]; /* an array of strings containing those arguments */
{@+unsigned long n=100; /* the desired number of vertices */
  unsigned long n_weight=0; /* the |north_weight| parameter */
  unsigned long w_weight=0; /* the |west_weight| parameter */
  unsigned long p_weight=0; /* the |pop_weight| parameter */
  unsigned long d=10; /* the |max_degree| parameter */
  long s=0; /* the random number seed */
  unsigned long r=1; /* the number of repetitions */
  char *file_name=NULL; /* external graph to be restored */
  @;
  while (r--) {
    if (file_name) g=restore_graph(file_name);
    else g=miles(n,n_weight,w_weight,p_weight,0L,d,s);
    if (g==NULL || g->n<=1) {
      fprintf(stderr,"Sorry, can't create the graph! (error code %ld)\n",
               panic_code); /* panic_code is set nonzero if graph
                             * generator panics. 
                             * panic_code indica o problema que ocorreu,
                             * veja gb_graph.w
                             */
      return -1; /* error code 0 means the graph is too small */
    }

Módulo GB_RAND

Copiado do arquivo módulo GB_RAND (gb_rand.w):

This GraphBase module provides two external subroutines called random_graph and random_bigraph, which generate graphs in which the arcs or edges have been selected ``at random.'' A third subroutine, random_lengths, randomizes the lengths of the arcs of a given graph. The performance of algorithms on such graphs can fruitfully be compared to their performance on the nonrandom graphs generated by other GraphBase routines.

[...]

The procedure

random_graph(n,m,multi,self,directed,dist_from,dist_to, min_len,max_len,seed)

is designed to produce a pseudo-random graph with n vertices and m arcs or edges, using pseudo-random numbers that depend on seed in a system-independent fashion. The remaining parameters specify a variety of options:
multi!=0 permits duplicate arcs;
self!=0 permits self-loops (arcs from a vertex to itself);
directed!=0 makes the graph directed; otherwise each arc becomes an undirected edge;
dist_from and dist_to specify probability distributions on the arcs;
min_len and max_len bound the arc lengths, which will be uniformly distributed between these limits.

If dist_from or dist_to are NULL, the probability distribution is uniform over vertices; otherwise the dist parameter points to an array of n nonnegative integers that sum to 230, specifying the respective probabilities (times 230) that each given vertex will appear as the source or destination of the random arcs.

[...]

Sugestão

Brinque com o seu programa, brinque muito. Aplique-o ao grafo de cidades brasileiras e a vários grafos do Stanford GraphBase (use as funções miles e random_graph. Durante a fase de testes, use grafos pequenos. Faça um desenho do grafo num pedaço de papel para conferir a resposta do seu programa.

Uso de WEB

Gostaria de destacar que o uso do WEB, segundo o seu criador D. Knuth, tem as seguintes finalidades de

Como conseqüência, Knuth comenta que fica mais divertido escrever programas.

Mudando de assunto, um comentário sobre comentários: ``Antes de cada função [e bloco] diga o que a função [e bloco] faz. Procure responder as perguntas que um usuário faria: que dados essa função recebe? que suposições faz sobre esses dados? que resultados devolve? Não perca tempo tentando dizer como a função faz o que ela faz.''(Paulo Feofiloff) Se o tamanho de seus blocos é razoavelmente pequeno, como deve ser, o conselho é extremamente útil.

Observação. Cópiei o comentário acima da página de grafos do prof. José Augusto

Entrega e Prazos

  1. Este exercício-programa vale 20 pontos.
  2. Como sempre, somente entregue seu programa se o mesmo não apresentar erros de compilação. O processo de compilação aqui deve ser entendido como todo o processo cweave, latex, ctangle (se você fez em CWEB) e gcc.
  3. Junto com o seu programa você deve entregar um Makefile de tal forma que
    meu_prompt> make fluxo.tex
    gere o documento fluxo.tex correspondente ao seu EP6,
    meu_prompt> make fluxo.dvi
    produza o fluxo.dvi correspondente ao seu EP6,
    meu_prompt> make fluxo.c
    crie o arquivo fluxo.c correspondente ao seu EP6, e
    meu_prompt> make fluxo
    produza o executável de nome fluxo correspondente ao seu EP6.
  4. O Panda não costuma aceitar a entrega de vários arquivos. Por isto, você deve criar um arquivo ep6.tar.gz com todo o seu trabalho. Espera-se que
    meu_prompt>tar -xvf ep6.tar
    crie um diretório que tenha o seu login na rede Linux como nome. Neste diretório devem estar todos os arquivos do seu EP6, inclusive o Makefile que você usou. Se você achar necessários coloque junto um arquivo 00-leia-me, onde você descreve algo que achar necessário: como limitações e bugs no seu programa.
  5. O seu EP6 deve ser depósitado no panda até o 24:00 do dia 07 JUL 2003.
[ Página principal de algoritmos em grafos. | Exercícios-programas]
Last modified: Fri Jun 20 14:29:46 EST 2003