TRABALHO DE GEOMETRIA COMPUTACIONAL
Professor: José Coelho de Pina
Índice
Planejamento de Movimento de Robôs
OBSERVAÇÃO: Em função de incompatibilidade das versões dos browsers, alguns símbolos podem aparecer distorcidos, entre eles, a intersecção.
MOTIVAÇÃO
Um dos objetivos atuais na robótica é fazer o design de robôs autônomos, ou seja, robôs que precisam, somente, saber O QUE fazer, sem que você precise contar COMO fazer. Entre outras coisas, isso significa que um robô tem de ser capaz de ´planejar´ seu próprio deslocamento.
Para planejar seu deslocamento, o robô deve ter conhecimento dos locais por onde está se movendo, dos obstáculos existentes e de objetos móveis que podem cruzar seu caminho (pessoas, outros robôs, etc). É necessária a colocação de sensores.
Utilizando informações sobre seu ambiente (ex.: planta do andar) e seus sensores, o robô consegue atingir seu destino sem que haja colisão.
O problema do deslocamento de robôs consiste em encontrar um caminho da origem ao destino, sem que o robô colida com objetos.
Para este problema, precisaremos fazer algumas simplificações. Para ter mais informações, veja em [1].
ESPAÇO DE TRABALHO E ESPAÇO DE CONFIGURAÇÃO
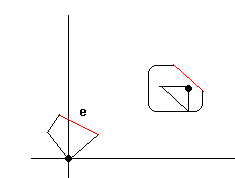
Definimos o robô de R, o espaço de trabalho, de S = {p1,..., pt}, onde pi (i=1,...,t) são os obstáculos. Assumimos que R é um polígono simples e vamos trabalhar, inicialmente, em 2-D (que é o espaço de trabalho). A localização (ou configuração) do robô pode ser especificada por um vetor de translação, cuja notação é R(x,y). Exemplo: se o robô é o polígono com vértices (1, -1), (1,1), (0,3), (-1,1) e (-1,-1), então os vértices de R(6,4) são (7,3), (7,5), (6,7), (5,5) e (5,3).
Outra maneira de denotar o movimento robótico pode ser através do ´ponto de referência´. É mais intuitivo se a origem (0,0) está no interior de R(0,0). Por definição, este é chamado o ponto de referência do robô. Em geral, o ponto de referência não precisa estar dentro do polígono determinado pelo robô, mas pode estar fora, e podemos imaginá-lo estar ´linkado´ com o robô por uma ligação invisível. Por definição, este ponto é a origem R(0,0).
ROTAÇÃO
Agora suponha que o robô possa sofrer rotação, ao redor do seu ponto de referência. Desta forma, é necessário um parâmetro extra, que vamos chamar de f , para especificar a orientação da rotação (mais precisamente, ângulo). Assim, R(x, y, f ) especifica o ponto de referência em (x, y) e rotação segundo um ângulo de f .
A localização de um robô é especificada por um número de parâmetros que correspondem ao número de graus de liberdade do robô. Este número é dois para robôs planares, os quais somente podem sofrer translação. Três para robôs planares que podem sofrer translação e rotação. Já para 3-D, em sendo o espaço maior, um robô que sofre somente translação tem 3 graus de liberdade. Um robô em 3-D que também sofre rotação tem 6 graus de liberdade.
Espaço de configuração da rotação
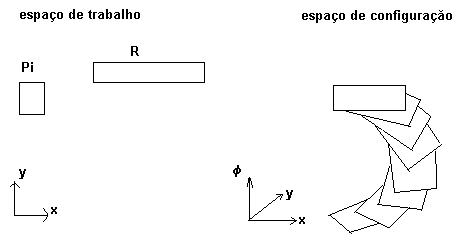
Denotado por C(R), o espaço de configuração é o espaço de parâmetros. Um ponto p no espaço de configuração corresponde a uma certa localização R(p) do robô no espaço de trabalho. Exemplo: no exemplo dado de translação e rotação do robô no plano, o espaço de configuração é 3-dimensional, não o espaço tri-dimensional Euclidiano, mas o espaço R x R x [0 : 360). Um ponto (x, y, f ), no espaço de parâmetros corresponde a uma localização R(x, y, f ) no espaço de trabalho. Assim, o espaço de configuração de um robô rotacional tem uma topologia especial, que é o cilindro.
O espaço de configuração de um robô translacional no plano é o bi-dimensional plano Euclidiano e, portanto, idêntico ao espaço de trabalho.
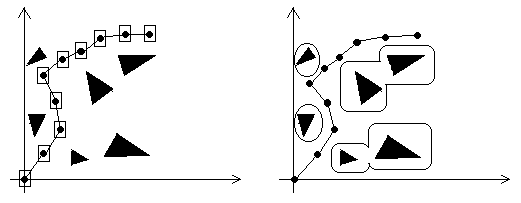
Assim, o espaço de trabalho é o espaço onde o robô move-se, ou seja, o mundo real. Já o espaço de configuração é o espaço de parâmetros do robô (ver desenho).

Na figura acima, o desenho da esquerda corresponde ao espaço de trabalho. O ponto origem dos planos é o ponto de referência. O desenho da direita corresponde ao espaço de configuração.
Há algumas regiões no espaço de configuração que vamos verificar:
Uma questão importante a ser tratada: se o robô APENAS TOCA um obstáculo, é considerada colisão?
A resposta é NÃO, ou seja, é permitido que o robô toque os obstáculos.
ROBÔ PUNTIFORME
Definimos o robô R e um conjunto de obstáculos p1,..., pt.
Os obstáculos são polígonos com interiores disjuntos, onde o total de vértices é n.
Nossa intenção é construir uma estrutura de dados que possa representar o espaço livre. Esta estrutura pode ser usada para computar o caminho entre 2 pontos quaisquer (origem e destino).
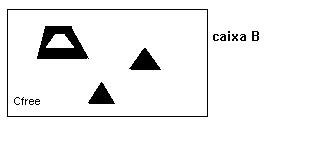
Para simplificar, vamos restringir o movimento do robô para uma ´caixa´ B, que contém os polígonos. Assim, Cfree passa a ser:
Cfree = B - U pi (i = 1,...,t) , onde pi é o i-obstáculo (veja desenho).
Nosso objetivo é encontrar uma representação do Cfree que nos permita achar o caminho entre qualquer ponto até qualquer destino. Vamos utilizar ´mapeamento trapezoidal´ para isso.
Cabe aqui um parêntesis: Mapeamento Trapezoidal
Um mapeamento trapezoidal é feito para facilitar localização de pontos no plano. A idéia é dividir o espaço em regiões (pedaços). Traçamos uma vertical passando em cada vértice de cada obstáculo. Retiramos os segmentos no interior dos polígonos.
O algoritmo devolve uma estrutura t(E) com as faces e suas arestas associadas.
Assim, um determinado ponto q pode ser localizado pelo pedaço e também pelos segmentos DENTRO do próprio pedaço. Os pedaços são ordenados crescentemente pelas x-coordenadas e também há uma ordenação de cima para baixo das regiões dentro dos pedaços, delimitadas pelos segmentos (arestas) do polígono. Este algoritmo leva tempo O(n).
Voltando à nossa teoria:
Algoritmo EspaçosLivres (S)
Entrada: conjunto de polígonos disjuntos S
Saída: mapeamento trapezoidal de Cfree(R, S) de um conjunto de pontos R do robô
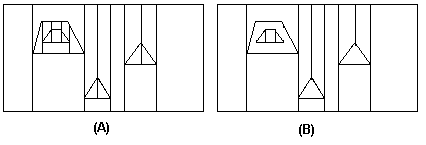
figura A: mapeamento trapezoidal após a linha 2 do algoritmo
figura B: mapeamento após a linha 3 do algoritmo (remoção de trapezóides no interior dos polígonos).
Análise do algoritmo
A linha 2 do algoritmo leva tempo O(n log n). Para maior aprofundamento no assunto, ver em [1], catp 6. Na linha 3, para remover os trapezóides que estão no interior dos polígonos que representam os obstáculos, levamos tempo constante, uma vez que, para isso, basta achar a aresta associada a cada trapezóide, utilizando a estrutura t(E) devolvida pelo algoritmo de trapezoidalização.
Para saber se devemos retirar ou não um trapezóide, é suficiente verificar se as arestas associadas ao obstáculo estão abaixo ou acima dele. Mas as arestas dos obstáculos são listadas em ordem, seguindo a estrutura t(E).
Lema
O algoritmo EspaçosLivres leva tempo O(n log n) para ser executado, onde n é o número de arestas dos obstáculos.
Mapa de caminhos
A primeira parte é o mapeamento trapezoidal do espaço livre: t (Cfree). Tendo isto, vamos construir o mapa de caminhos Groad. Assim, já estaremos falando em encontrar um caminho entre um ponto origem e um ponto destino.
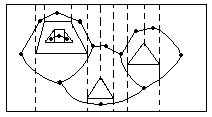
Para obter este mapa, fazemos o seguinte: achamos o centro de cada trapezóide e o marcamos com um ponto. Também colocamos um ponto no meio de cada extensão vertical (ver desenho).
Este mapa pode ser construído em tempo O(n), utilizando a estrutura t (Cfree).
Podemos ir de um nó no centro de um trapezóide para outro nó no centro de outro trapezóide vizinho através de um ponto no limite da extensão vertical que os separa.
Para determinar o caminho entre Porigem e Pdestino, fazemos o seguinte: primeiramente, achamos os trapezóides onde estão Porigem e Pdestino. Estes são indicados por D origem e D destino, respectivamente. Se D origem = D destino, ou seja, a origem e o destino estão no mesmo trapezóide, então basta-nos movermos de Porigem para Pdestino por uma linha reta entre eles. Se não estiverem no mesmo trapezóide, devemos achar Vorigem e Vdestino, que são o centro de D origem e D destino, respectivamente. Assim, dividimos o nosso problema em três partes: encontrar um caminho de Porigem a Vorigem (como estão no mesmo trapezóide, é só traçar uma linha reta entre eles); encontrar (no Groad), o caminho entre Vorigem e Vdestino e encontrar o caminho entre Vdestino e Pdestino (linha reta).
Segue o algoritmo:
Algoritmo AchaCaminho(t (Cfree), Groad, Porigem, Pdestino)
Entrada: mapa trapezoidal t (Cfree) do espaço livre, o mapa de caminhos Groad, Porigem e Pdestino.
Saída: um caminho entre Porigem e Pdestino, se existir. Se não existir, relata o fato.
Corretude do algoritmo
Para provar que não há colisões, é simples: como estamos lidando com o mapa trapezoidal do espaço livre, para onde quer que caminhemos na estrutura, sabemos que, se o caminho é possível, o mesmo está no espaço livre, ou seja, NÃO vai colidir com nenhum obstáculo.
Suponha que há um caminho entre Porigem e Pdestino. Estes pontos pertencem ao trapezóide do espaço livre, portanto, resta-nos provar que há um caminho em Groad entre Vorigem e Vdestino
O caminho de Porigem a Pdestino deve passar por uma sequência de trapezóides D i = D 2, D 3,…, D k = D destino, onde Vi é o vértice de Groad que está no centro do trapezóide D i. Se o caminho passa de D i para D i+1, então estes são vizinhos e, portanto, dividem uma extensão vertical. Mas Groad é contruída tendo como base que os nós dos trapezóides são conectados por um vértice que está no limite. Assim, EXISTE um caminho em Groad de Vi para Vi+1. Podemos aplicar o mesmo raciocínio de V1 até Vk. Assim, garantimos que a busca em largura, certamente, encontrará um caminho de Vorigem a Vdestino, se existir…
Complexidade do algoritmo
Achar os trapezóides de Porigem a Pdestino leva tempo O(log n), usando a estrutura t (E). Alternativamente, poderíamos buscar um a um na estrutura, de modo que leva tempo linear, o que não vai fazer diferença no final das contas.
A busca em largura leva tempo linear em Groad, que tem um vértice por trapezóide, mais um vértice por extensão vertical. Tanto o número de trapezóides quanto o de extensões são lineares no número total de vértices dos obstáculos. Assim, o tempo gasto é O(n).
O tempo para indicar (imprimir) o caminho está associado ao número máximo de arcos no caminho, que é O(n).
Resumo
TOTAL DE TEMPO DO ALGORITMO: O(n log n)
SOMAS DE MINKOVSKI
Na parte anterior, estudamos o movimento de um robô puntiforme. Agora, vamos tratar o robô como sendo um polígono. Vamos assumir que o robô R é convexo, assim como os obstáculos são. O espaço de configuração do obstáculo (C-obstáculo) P e o robô R são o conjunto de pontos no espaço de configuração que corresponde à localização em que R intersecta P. Notação: denotamos o C-obstáculo de P por Cp.
Cp := { (x,y) : R(x,y) ∩ P ¹ Æ }
Pode-se visualizar o formato de Cp deslizando R ao redor dos limites de P. Podemos descrever (expressar) os C-obstáculos abaixo:
S1 Å S2 := { p + q: p Î S1, q Î S2}; p = (px, py) e q = (qx, qy) Þ p + q = (px + qx, py + qy}
A soma de Minkovski aplica-se à modelagem porque polígonos são planares.
Outras definições:
Teorema
Defina R, robô translacional, polígono e defina P como obstáculo. O C-obstáculo de P é P Å (-R(0,0)).
Prova:
Temos de provar que R(x,y) intersecta P Û (x,y) Î P Å (-R(0,0)).
(Þ ) Suponha que R(x,y) intersecta P.
Defina q = (qx, qy) ponto de R ∩ P Þ q Î R(x,y) E q Î P.
Assim, como q Î R(x,y), temos que (qx – x, qy – y) Î R(0,0) Þ (-qx + x, -qy + y) Î -R(0,0).
Como q Î P Þ (x,y) Î P Å (-R(0,0)).
(Ü ) Defina (x,y) Î P Å (-R(0,0)).
Então há pontos (rx, ry) Î R(0,0) e (px, py) Î P tais que (x,y) = (px – rx, py – ry), ou seja, px = rx + x e py = ry + y, implicando que R(x,y) intersecta P. CQD ■
Propriedades da soma de Minkovski
Cp := P Å R. Um ponto extremo na direção d de Cp é a soma dos pontos extremos, na direção d, de P e R.
Teorema 3
P e R polígonos convexos com n e m arestas, respectivamente. Então, P Å R é um polígono convexo com pelo menos n + m arestas.
Prova
A convexidade segue diretamente da definição.
Verificando o número de arestas: considere uma aresta extrema e de P Å R. Deve ser gerada por pontos em P e R que são extremos na mesma direção. Ademais, pelo menos P ou R devem ter uma aresta extrema naquela direção. Vamos chamá-la de e. Desta forma, cada aresta é associada a pelo menos uma (de P ou R), de modo que o número total de arestas é pelo menor n + m. Se P e R não tiverem arestas paralelas, esse número é exatamente n + m.
Assim: a soma de Minkovski de 2 polígonos convexos é convexa e tem complexidade linear.
Vamos escrever, abaixo, o algoritmo de soma de Minkovski. Um algoritmo é: " para (v,w) de vértices, v Î P e w Î R, execute v + w. Após, execute o fecho convexo de todas essas somas. Este algoritmo é ineficiente quando o polígono tem muitos vértices, porque o algoritmo olha para todo par de vértices.
Um algoritmo alternativo: olha somente a pares de vértices que são extremos na mesma direção. No algoritmo, usaremos a notação ângulo(pq) para denotar o ângulo pq com o eixo x.
Algoritmo SomaDeMinkovski (P, R)
Entrada: polígonos convexos: P com vértices v1,…, vn
Q com vértices w1,…, wn
Vértices ordenados no sentido horário, com v1 e w1 sendo os vértices com menor y-coordenada.
Saída: soma de Minkovski P Å R.
Corretude do algoritmo
Como a prova do teorema 3, qualquer vértice da soma de Minkovski é a soma de 2 vértices originais com extremos numa direção comum. Os testes de ângulos do algoritmo asseguram que todos os pares extremos são encontrados.
Complexidade do algoritmo
Teorema 4
A soma de Minkovski de 2 polígonos convexos com n e m vértices, respectivamente, pode ser executada em tempo O(n + m).
Soma de Minkovski para polígonos não-convexos
Até agora, só estudamos a soma de Minkovski para polígonos convexos. A partir daqui, vamos considerar polígonos não-convexos. Para tanto, vamos trabalhar com a seguinte propriedade, para S1, S2 e S3:
S1 Å (S2 U S3) = (S1 Å S2) U (S1 Å S3)
Vamos considerar, agora, a soma de Minkovski entre um polígono não-convexo P com n vértices e um polígono convexo R com m vértices.
Sabemos que P pode ser triangularizado com n – 2 triângulos t1,…, tn-2.
Da equação acima, temos que: P Å R = U ti Å R (para i = 1,..., n-2).
Se ti é triângulo e R é polígono convexo com m vértices, sabemos que ti Å R é um polígono convexo com pelo menos m + 3 vértices. Ademais, os triângulos são disjuntos. Consequentemente, a complexidade desta união (dos triângulos) é linear na soma das complexidades, ou seja, P Å R é O(nm).
Com dois polígonos NÃO-CONVEXOS, basta triangularizarmos P com n vértices e R com m vértices em (n-2) triângulos ti e (m-2) triângulos uj. A soma de Minkovski de P e R é a união das somas de Minkovski dos pares ti uj. Cada soma ti Å uj tem O(1). Como temos a união de (n-2) com (m-2) componentes, a complexidade de tempo no pior caso é O(n * n + m * m).
Teorema 5
Defina P e R polígonos com n e m vértices, respectivamente.
A complexidade da soma de Minkovski P Å R é:
DESLOCAMENTO TRANSLACIONAL
Vamos relembrar que um C-obstáculo corresponde à soma de Minkovski de um obstáculo Pi Å (-R).
Pseudodiscos
Um par o1, o2 de objetos planares formam um par de pseudodiscos se satisfaz à propriedade:
Exemplo:

Para qualquer par de pseudodiscos, há pelo menos 2 intersecções próprias entre as fronteiras.
Vamos provar que uma coleção de somas de Minkovski formam uma coleção de pseudodiscos.
Obs. 4: Defina P1 e P2 polígonos convexos com interiores disjuntos. Defina d1 e d2 direções nas quais P1 é mais extremo que P2. Então, P1 é mais extremo que P2 nas direções do intervalo [d1, d2] ou nas direções do intervalo [d2, d1].
Teorema 8
Defina P1 e P2 polígonos convexos com interiores disjuntos e defina R, outro polígono convexo. Então as 2 somas de Minkovski P1 Å R e P2 Å R são psedodiscos.
Prova
Cp1 := P1 Å R e Cp2 := P2 Å R
Por simetria, é suficiente mostrar que Cp1 – Cp2 é conexo.
Como Cp1 e Cp2 são convexos, um componente conexo de Cp1 – Cp2 deve conter um ponto no fecho convexo de Cp1 U Cp2. Se há mais do que um componente conexo, então deve haver 2 direções d1 e d2 tais que Cp1 é mais extremo nestas direções do que Cp2.
Obs. 5: Define P e R dois objetos no plano, Cp := P Å R. Um ponto extremo na direção d de Cp é a soma dos pontos extremos na direção d de P e R.
Desta obs 5, segue que P1 é mais extremo que P2 nestas 2 direções.
Da obs anterior (obs4), P1 é mais extremo que P2 nas direções do intervalo [d1, d2 ] ou nas direções do intervalo [d2, d1 ].
Utilizando a obs5 acima, o conjunto de direções para as quais os pontos extremos em Cp1 estão mais afora que Cp2 é conexo, contradizendo nossas hipóteses que há 2 componentes conexos.
Teorema 9
Define S como uma coleção de pseudodiscos poligonais com n arestas ao total. A complexidade da união deles é O(n).
Prova
Vamos provar que todo vértice da união dos pseudodiscos é verificado ao máximo 2 vezes. Complexidade 2n, ou seja, O(n).
Há dois tipos de vértices a serem verificados: vértices do pseudodisco e intersecção de arestas dos pseudodiscos.
Pontos (vértices) de intersecção: considere vértice v da união, que é intersecção da aresta e de um pseudodisco P Î S e outra aresta e’, de P’ Î S. Imagine que estas arestas entram em outro pseudodisco e se encontram em v. Siga e até o interior de P’. Se ele termina no interior, então verificamos v até o final de e, no interior de P’. O ponto onde isto acontece é a intersecção dos limites de P e P’. Junto com v, faz 2 pontos de intersecção, de modo que e’ não deixa o interior de P sem violar a propriedade dos pseudodiscos. Consequentemente, e’ tem um vértice dentro de P, tendo sido verificado o vértice v.
Neste raciocínio, cada vértice do pseudodisco é verificado 2 vezes.
Para os vértices no limite: verificação é trivial.
Teorema 15
Defina R um robô convexo de complexidade constante, translade-o sobre um conjunto S de obstáculos poligonais que não se intersectam, com um total de n arestas. A complexidade para achar o espaço de configuração livre (Cfree(R,S)) é O(n).
Prova
Triangularize cada polígono que é obstáculo. Obteremos O(n) triangulos convexos, obstáculos com interiores disjuntos. O espaço de configuração livre é o complemento da união dos C-obstáculos desses triângulos. Como o robô tem complexidade constante, os C-obstáculos têm complexidade constante, de acordo com o teorema 8. Assim, o teorema 9 implica que a união tem complexidade O(n).
Vamos mostrar um algoritmo que encontra os espaços ocupados. O espaço livre é o complemento deste conjunto.
Devemos lembrar que: Cforb = U Cpi = U Pi Å (-R(0,0)) para i = 1,..., n
Algoritmo EspaçoOcupado (Cp1,…, Cpn)
Entrada: coleção de C-obstáculos
Saída: espaços ocupados Cforb = U Cpi (para i = 1,..., n)
Complexidade do algoritmo
LEMA:
O espaço de configuração livre de um robô convexo de complexidade constante, transladando sobre um conjunto S de polígonos com n arestas ao total pode ser executado em tempo O(n log n).Prova
Tempo para triangularização de um polígono com m vértices: O (m log m)
mi é a complexidade do obstáculo Pi.
S mi log mi <= S mi log n = n log n (para i = 1,..., t)
A linha 5 do algoritmo leva tempo O(n log n).
Como trata-se de um algoritmo de divisão e conquista, então a recorrência é:
T(n) = T(é n/2ù ) + T(ë n/2û ) + O(n log n)
Assim, a solução da recorrência é O(n log log n).
Este resultado NÃO é o melhor possível (não é ótimo).
Para termos o caminho entre um ponto Porigem e seu Pdestino, basta seguirmos como feito na seção anterior (para robô puntiforme). Definimos o mapa trapezoidal Groad, etc….
Teorema
Defina R robô convexo de complexidade constante transladando sobre um conjunto S de obstáculos poligonais disjuntos com n arestas ao total. Um pré-processamento leva tempo O(n log log n) e o caminho entre um Porigem até Pdestino, se existir, pode ser obtido em tempo linear.
DESLOCAMENTO COM ROTAÇÃO
Mesmo modelo: R é robô polígono convexo, que pode sofrer translação e rotação num espaço planar com P1,…,Pt obstáculos poligonais disjuntos.
Agora, R tem 3 graus de liberdade: R x R x [0:360) ® R(x, y, f ).
Assim: Cpi := {(x, y, f ) Î R x R x [0:360) : R(x, y, f ) Ç Pi ¹ Æ }
Aparência dos obstáculos
No plano com ângulo de rotação fixado, f = f0, a forma de secção cruzada é uma soma de Minkovski. Mais precisamente, uma secção cruzada de Cpi com o plano h: f = f 0 é:
Pi Å R(0, 0, f 0) Þ soma de Minkovski na altura f 0.
Agora imagine uma varredura num plano horizontal do espaço de configuração, começando em f = 0 até f = 360º. Em qualquer momento, a secção cruzada da varredura do plano com Cpi é uma soma de Minkovski.
A forma destas somas de Minkovski mudam continuamente, desde f = f 0, onde a secção cruzada é Pi Å R(0, 0, f 0) até f = f 0 + e , onde a secção é Pi Å R(0, 0, f 0 + e ). Isto significa que Cpi parece um pilar torcido. As arestas e faces deste pilar torcido, exceto no topo e na base, são curvas.
Nossa tática de construir o mapa de estradas e dividir o percurso de Porigem e Pdestino em partes, continuará a ser utilizada.
No entanto, vamos mudar nossa modelagem. Como falamos há pouco, cada secção cruzada vai se chamar fatia. A idéia é trabalhar com um número finito de fatias.
Um caminho do robô agora consiste de 2 tipos de deslocamento: dentro da fatia – que é um deslocamento puramente translacional – e de uma fatia para outra – que implica deslocamento rotacional.
Uma fatia é uma secção cruzada – plano.
Formalizando:
z é o número de fatias
" i Î N, 0 <= i <= Z, f i = i x (360 / z)
Executaremos uma fatia do espaço livre para cada f i.
Então, dentro de uma fatia, estaremos falando de deslocamento translacionais para o robô R(0, 0, f i) e usamos os métodos estudados até agora. Isto nos dará um mapa trapezoidal t i do espaço livre desta fatia. E para cada t i, teremos um mapa de estradas Gi.
Movimento entre fatias: conectamos os mapas de estradas Gi, Gi+1 para obter o mapa de estradas geral Groad do espaço de configuração inteiro. Quando adicionamos um nó extra para Groad em (x, y, f i) e em (x, y, f i+1), estão conectados por um arco. O movimento de uma fatia para outra é um movimento de rotação de f i para f i+1.
Assim, utilizaremos a seguinte técnica para achar um caminho de R(Xorigem, Yorigem, f origem) para R(Xdest, Ydest, f dest):
Algoritmo AchaCaminhoRotacional
Se um destes trapezóides não existir (porque podem estar no espaço ocupado), relatamos o fato.
Assim, temos agora o caminho consistindo de 5 partes:
Corretude do algoritmo
Este algoritmo NEM SEMPRE está correto. Algumas vezes, pode relatar erroneamente que um caminho não existe. Por exemplo: a posição inicial pode estar no espaço livre, mas a posição inicial projetada na fatia mais próxima não está num espaço livre. Neste caso, relatamos que há um caminho, quando na verdade não há.
Livre de colisão: nos movimentos rotacionais (de uma fatia para outra) pode haver problemas: as localizações dentro das 2 fatias podem ser livres de colisão. No entanto, neste caminho entre as duas fatias, pode haver colisão. Ambos os problemas são menos prováveis de ocorrer à medida que aumenta-se o número de fatias, porém nunca teremos certeza da corretude do resultado.
Para evitar estes problemas, podemos usar um truque. Fazemos o robô levemente mais largo e utilizamos o método descrito para o robô alargado R’. Embora R’ possa colidir durante as rotações, o robô original R não colide.
O ‘alargamento’ do robô é feito da seguinte maneira: rotacione o robô R nos sentidos horário e anti-horário num ângulo de (180º / z).
Utilizamos R’, ao invés de R, no algoritmo acime, nos mapas trapezoidais e mapas de estradas. Veja figura:
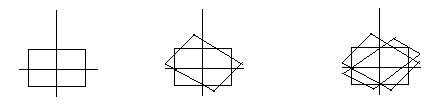
Esta técnica, com um grande número de fatias, na prática funciona muito bem.
Comentários
O problema do deslocamento de robôs tem sido alvo de muitas pesquisas e estudos. Em alguns livros, pode-se encontrar uma literatura muito mais elaborada do que o que foi visto aqui. Em J.C. Latombe, Robot Motion Planning, Kluwer Academic Publishers, Boston ’91 há estudos mais intensivos.
BIBLIOGRAFIA
[1] Computational Geometry