


Next: About this document ...
MAC-IME-USP CARLOS EDUARDO FERREIRA
SALA 297A TEL.: 3818 6140
E-MAIL cef@ime.usp.br
MONITOR: MARCIO C. CABRAL
MAC 122 - Princípios de Desenvolvimento de Algoritmos
Segundo semestre de 2000
Lista de exercícios--Recursão
``Para fazer uma função recursiva
é preciso ter fé.''
Siang Wun Song
- Faça uma função recursiva MaxMin que calcula o elemento máximo e o
elemento mínimo de um vetor com
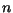 números inteiros.
números inteiros.
- Quantas comparações (em função de
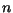 ) envolvendo elementos do vetor o
seu algoritmo faz?
) envolvendo elementos do vetor o
seu algoritmo faz?
- Faça uma função recursiva Dígito que recebe um número inteiro
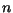 e
calcula a soma dos digitos de
e
calcula a soma dos digitos de 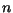 . Exemplo: se
. Exemplo: se 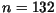 então Dígito
então Dígito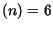 .
.
- Faça uma função recursiva que verifica se uma expressão de
parênteses é bem formada.
- Idem para uma expressão com parênteses, colchetes (`[',`]') e chaves
(`{',`}').
- Considere a função abaixo:
double f(double x, double y)
{
if (x >= y)
return ((x+y)/2);
return (f(f(x+2, y-1), f(x+1, y-2));
}
Qual é o valor de 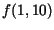 ? Como se poderia calcular
? Como se poderia calcular 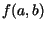 de maneira mais
simples?
de maneira mais
simples?
- A função de Akermann é definida da seguinte maneira:
Escreva uma função recursiva que recebe inteiros não negativos 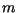 e
e 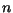 e
devolve
e
devolve 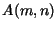 .
.
- Simule a execução do programa abaixo:
#include <stdio.h>
int fusc(int n)
{
if (n <= 1) return (1);
if (n % 2 == 0)
return( fusc(n / 2) );
return( fusc((n-1)/2) + fusc((n+1)/2) );
}
int main()
{
int m = 7;
printf("Fusc = %d\n", fusc(m));
}
- Considere a seguinte função:
void misterio (int A[], int inic, int fim)
{
int aux;
while (A[fim] % 2 == 0 && inic < fim)
fim --;
while (A[inic] % 2 == 1 && inic < fim)
inic++;
if (inic < fim){
aux = A[inic];
A[inic] = A[fim];
A[fim] = aux;
misterio(A, inic, fim);
}
}
- Simule a função Mistério para
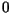 |
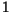 |
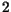 |
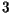 |
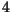 |
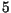 |
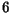 |
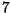 |
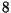 |
|
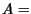 |
8 |
10 |
3 |
6 |
5 |
2 |
9 |
1 |
4 |
Inicio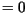 e Fim e Fim 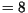 . . |
- O que faz a função Mistério? Quantas comparações envolvendo elementos
do vetor
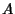 são feitas? Escreva um algoritmo que faz a mesma coisa com um
número menor de comparações.
são feitas? Escreva um algoritmo que faz a mesma coisa com um
número menor de comparações.
- Simule a seguinte função recursiva para
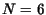 :
:
int zzz(int n)
{
int aux;
if (n <= 2)
return(1);
n--;
aux = zzz(n);
n--;
return (aux + zzz(n));
}
- Escreva uma função recursiva Tab
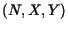 que recebe como parâmetro um
inteiro não negativo
que recebe como parâmetro um
inteiro não negativo 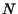 e calucula um par de inteiros
e calucula um par de inteiros 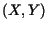 , onde
, onde 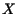 e
e 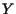 são as coordenadas de
são as coordenadas de 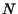 na tabela abaixo:
na tabela abaixo:
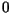 |
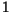 |
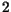 |
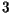 |
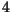 |
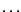 |
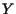 |
| 0 |
0 |
2 |
5 |
9 |
14 |
|
|
| 1 |
1 |
4 |
8 |
13 |
|
|
|
| 2 |
3 |
7 |
12 |
|
|
|
|
| 3 |
6 |
11 |
|
|
|
|
|
| 4 |
10 |
|
|
|
|
|
|
| ... |
|
|
|
|
|
|
|
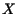 |
|
|
|
|
|
|
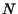 |
- Suponha que temos de calcular o produto de matrizes
onde cada 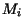 é uma matriz com
é uma matriz com 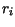 linhas e
linhas e 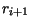 colunas. (Portanto,
colunas. (Portanto,
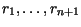 descrevem as dimensões das matrizes.) Suponha ainda que o
produto de qualquer par de matrizes será calculado pelo algoritmo usual; assim
o produto de uma matriz
descrevem as dimensões das matrizes.) Suponha ainda que o
produto de qualquer par de matrizes será calculado pelo algoritmo usual; assim
o produto de uma matriz 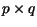 por uma matriz
por uma matriz 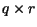 requer
requer
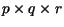 operações de multiplicação entre números. A ordem em que
a multiplicação de três ou mais matrizes é executada pode afetar
sensivelmente o número total de multiplicações. Por exemplo, se
operações de multiplicação entre números. A ordem em que
a multiplicação de três ou mais matrizes é executada pode afetar
sensivelmente o número total de multiplicações. Por exemplo, se 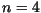 e
e
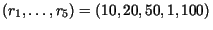 então o cálculo da expressão
então o cálculo da expressão
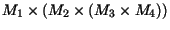 requer 125000 multiplicações enquanto que
o cálculo da expressão
requer 125000 multiplicações enquanto que
o cálculo da expressão
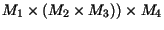 requer 2200
multiplicações. Seja
requer 2200
multiplicações. Seja 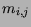 o número mínimo de multiplicações necessárias
para calcular
o número mínimo de multiplicações necessárias
para calcular
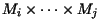 . Temos que
. Temos que
Escreva uma função recursiva que recebe 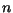 e a seqüência
e a seqüência
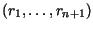 e calcula
e calcula 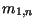 .
.
- Escreva uma função que dado
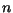 imprime todas as permutações
dos números inteiros
imprime todas as permutações
dos números inteiros 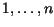 . Escreva duas versões,
uma iterativa e uma recursiva. (Sugestão: O conjunto das
permutações dos inteiros
. Escreva duas versões,
uma iterativa e uma recursiva. (Sugestão: O conjunto das
permutações dos inteiros 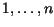 pode ser obtida através
do conjunto das permutações dos inteiros de
pode ser obtida através
do conjunto das permutações dos inteiros de
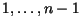 inserindo-se
inserindo-se 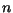 em cada possível posição de cada permutação.)
em cada possível posição de cada permutação.)
- Escreva uma função que dados dois inteiros positivos
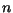 e
e 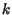 imprima
todas as combinações de
imprima
todas as combinações de 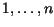 em grupos de tamanho
em grupos de tamanho 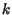 . Escreva duas
versões, uma iterativa e outra recursiva.
. Escreva duas
versões, uma iterativa e outra recursiva.
- Escreva um programa para imprimir em ordem lexicográfica todos os subconjuntos
do conjunto
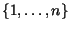 . Para
. Para
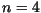 o resultado deve ser:
o resultado deve ser:
- A função abaixo calcula o maior divisor comum dos inteiros positivos
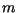 e
e 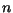 . Escreva uma função recursiva equivalente.
. Escreva uma função recursiva equivalente.
int Euclides (int m, int n)
{
int r;
do{
r = m % n;
m = n;
n = r;
}
while (r != 0);
return(m);
}



Next: About this document ...
Carlos Eduardo Ferreira
2000-10-02
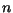 números inteiros.
números inteiros.
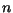 ) envolvendo elementos do vetor o
seu algoritmo faz?
) envolvendo elementos do vetor o
seu algoritmo faz?
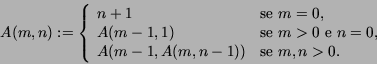
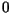
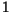
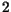
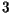
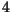
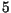
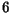
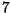
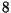
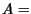
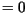 e Fim
e Fim 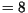 .
. são feitas? Escreva um algoritmo que faz a mesma coisa com um
número menor de comparações.
são feitas? Escreva um algoritmo que faz a mesma coisa com um
número menor de comparações.